第23讲 矩形 2025年中考一轮数学专题复习课件(湖南)(共24张PPT)
文档属性
| 名称 | 第23讲 矩形 2025年中考一轮数学专题复习课件(湖南)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:15:24 | ||
图片预览








文档简介
(共24张PPT)
第23讲 矩形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第五单元 第23讲
课标要求 作业目标
矩形 1.理解矩形的概念. 2.探索并证明矩形的性质定理:矩形的四个角都是直角,对角线相等. 3.探索并证明矩形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形. 掌握矩形的概念及性质定理,并能运用它们解决几何证明问题和生活应用问题
掌握直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”,并能运用它解决几何证明问题和简单的实际问题
掌握矩形的判定定理,并能运用它们解决几何证明问题和简单的实际问题
会分析矩形和平行四边形之间的区别和联系,进一步认识一般与特殊的关系
在综合的实际问题情境中抽象出数学模型,建立形数之间的联系
要求与目标
教材整合 核心归纳
02
第五单元 第23讲
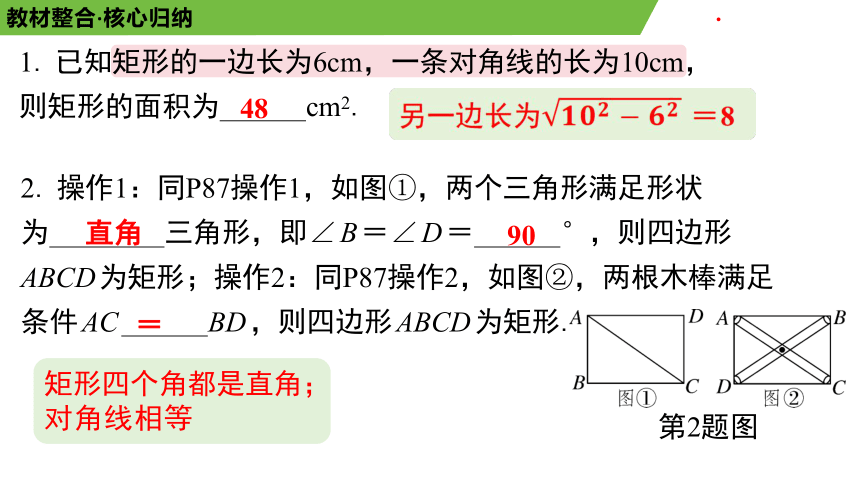
2. 操作1:同P87操作1,如图①,两个三角形满足形状
为 三角形,即∠B=∠D= °,则四边形
ABCD为矩形;操作2:同P87操作2,如图②,两根木棒满足
条件AC BD,则四边形ABCD为矩形.
48
直角
90
=
第2题图
1. 已知矩形的一边长为6cm,一条对角线的长为10cm,
则矩形的面积为 cm2.
另一边长为 =8
矩形四个角都是直角;
对角线相等
定义 平行四边形 矩形
性质 特殊的平行四边形:矩形具有平行四边形的所有性质;
角:四个角都是直角,即∠ABC=
∠BCD=∠ADC=∠BAD= ;
对角线:对角线互相平分且相等,即AC=BD,
OA=OC= = ;
对称性:既是中心对称图形,又是轴对称图形,有两条对称轴
90°
OB
OD
面积 面积:S= (a,b分别表示矩形的长和宽)
教材典型应用 如右图,已知点P为矩形边AD上任意一点,
PE⊥AC,PF⊥BD,则连接PO,根据面积法可
得出PE+PF是一个定值.见P92T10
ab
考点 矩形的性质【省卷T26,长沙T23】
考点清单
判定 判定方法 几何语言
有一个角是直角的平行四边形 ∵∠CDA= °,
四边形ABCD是平行四边形,
∴四边形ABCD是矩形
对角线相等的平
行四边形 ∵AC BD,
四边形ABCD是平行四边形,
∴四边形ABCD是矩形
有三个角是直角
的四边形 ∵∠CDA=∠DAB=
∠ABC= °,
∴四边形ABCD是矩形
90
=
90
考点 矩形的判定
考点清单
重难精讲
变式探究
03
第五单元 第23讲
例 改编问题链如下图, ABCD的对角线AC,BD相交于点O,已知AB=4.
(1)若△AOB是等边三角形.
①求证: ABCD是矩形;②求AD的长;
①证明:∵△AOB为等边三角形,∴OA=OB.
∵四边形ABCD是平行四边形,
∴OB=OD= BD,OA=OC= AC.
∴BD=AC. ∴ ABCD是矩形.
②解:∵ ABCD是矩形,∴∠BAD=90°.
∵△AOB为等边三角形,
∴∠ABO=60°.∴∠ADB=90°-60°=30°.
∴AD= AB=4 .
OA=OB
AC=BD
AD=ABtan60°
(2)【逆向设问】若∠BAD=90°,∠ABD=60°,求△AOB
的周长.
例 改编问题链如下图, ABCD的对角线AC,BD相交于点O,
已知AB=4.
解:∵四边形ABCD是平行四边形,
∠BAD=90°,
∴ ABCD是矩形.∴AC=BD. ∴OB=
BD= AC=OA.
又∵∠ABO=60°,∴△AOB为等边三角形.
∴△AOB的周长为12.
ABCD是矩形
OA=OB
△AOB为等边三角形
△AOB的
周长为12
1. (2024·成都)如下图,在矩形ABCD中,对角线AC与BD相交
于点O,则下列结论一定正确的是( C )
A. AB=AD
B. AC⊥BD
C. AC=BD
D. ∠ACB=∠ACD
第1题图
C
2. (2024·吉林)如下图,在平面直角坐标系中,点A的坐标为
(-4,0),点C的坐标为(0,2).以OA,OC为边作矩形OABC.
若将矩形OABC绕点O顺时针旋转90°,得到矩形OA'B'C',
则点B'的坐标为( C )
A. (-4,-2) B. (-4,2)
C. (2,4) D. (4,2)
第2题图
C
(-4,2)
-4
2
(2,4)
3. (2023·湘西州)如图,在矩形ABCD中,点E在边BC上,点F是AE的中点,AB=8,AD=DE=10,
则BF的长为 .
2
8
10
10
10
6
8
4
BF=AE
在Rt△DEC 中
EC==6
BE=4
在Rt△ABE中,
AE==4
BF=2
4. 如下图,将矩形ABCD沿对角线AC折叠,点B的对应点为
点E,AE与CD交于点F. 求证:△DAF≌△ECF.
第4题图
证明:将矩形ABCD沿对角线AC折叠,
则AD=BC=EC,
∠D=∠B=∠E=90°.
在△DAF和△ECF中,
∴△DAF≌△ECF(AAS).
5. 要检验一个四边形的桌面是否为矩形,可行的测量方案是
( C )
A. 测量两条对角线是否相等
B. 度量两个角是否是90°
C. 测量两条对角线的交点到四个顶点的距离是否相等
D. 测量两组对边是否分别相等
C
6. (2023·岳阳)如下图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
第6题图
(1)你添加的条件是 (填序号);
①(或②)
(2)添加条件后,请证明 ABCD为矩形.
添加条件①.
添加条件①.
证明:∵四边形ABCD是平行四边形,
∴∠A+∠D=180°.
在△ABM和DCM中,
∴△ABM≌△DCM(SAS).
∴∠A=∠D. ∴∠A=∠D=90°.
∴ ABCD为矩形.(选②证明也可)
易得△ABM≌△DCM(SAS)
∠A=∠D=90°
∠A+∠D=180°
AB=DC
∴AB∥DC,AB=DC.
ABCD为矩形
易得△ABM≌△DCM(SSS)
7. (2024·兰州)如下图,在△ABC中,AB=AC,点D是BC的中点,
CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE是矩形;
第7题图
证明:∵在△ABC中,AB=AC,点D是BC的中点,
∴AD⊥BC,
即∠ADC=∠ADB=90°.
∵CE∥AD,
∴∠ECD=∠ADB=90°.
∵AE⊥AD,
∴∠EAD=90°.
∴∠ADC=∠ECD=∠EAD=90°.
∴四边形ADCE是矩形.
三线合一
∠ADB=∠ADC=90°
∠ECD=∠ADB=90°
∠EAD=90°
四边形ADCE是矩形
(2)若BC=4,CE=3,求EF的长.
7. (2024·兰州)如下图,在△ABC中,AB=AC,点D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
解:∵在△ABC中,AB=AC,点D是BC的中点,BC=4,
∴BD=CD= BC=2.
由(1)可知四边形ADCE是矩形,
∴AE=CD=2,∠AEC=90°.
在Rt△AEC中,AE=2,CE=3,
由勾股定理得AC= = .
∵EF⊥AC,由三角形的面积公式得
S△AEC= AC·EF= AE·CE,
∴EF= = = .
3
3
2
2
面积法
S△AEC= AC·EF= AE·CE
2
由勾股定理得AC =
EF=
8. 如下图,矩形ABCD中,AB=2,点E是AC的中点,
∠AED=120°,则AD的长为( A )
A. 2 B. 4 C. 3 D. 5
第8题图
A
9. 矩形ABCD的对角线AC,BD相交于点O,点F在矩形
ABCD的边上,连接OF. 若∠ADB=38°,∠BOF=30°,
则∠AOF的度数为 .
10. 【面积法】如图,在矩形ABCD中,已知AD=12,
AB=5,点P是AD边上任意一点,PE⊥AC,PF⊥BD,点E,
F分别是垂足,则PE+PF的长为 .
46°或106°
第10题图
11. (2024·长沙)如下图,在 ABCD中,对角线AC,BD相交
于点O,∠ABC=90°.
(1)求证:AC=BD;
(1)证明:∵四边形ABCD是平行四边形,
∠ABC=90°,
∴四边形ABCD是矩形.
∴AC=BD.
证明:∵四边形ABCD是平行四边形,
∠ABC=90°,
∴四边形ABCD是矩形.
∴AC=BD.
解:如图,作OH⊥BC于点H,则∠OHE=∠OHC=90°.
∵∠ABC=90°,AB=6,BC=8,
∴AC= = =10.
∴OC=OA= AC=5.
∵∠CEO=∠COE,∴CE=OC=5.
∵OC=OA= AC,OB=OD= BD,且AC=BD,∴OC=OB.
∴HC=HB= BC=4.
∴EH=CE-HC=5-4=1.
∵ = =tan∠ACB,
11. (2024·长沙)如下图,在 ABCD中,对角线AC,BD相交于点O,∠ABC=90°.
(2)点E在BC边上,满足∠CEO=∠COE. 若AB=6,BC=8,
求CE的长及tan∠CEO的值.
∴OH= ·HC= ×4=3.
∴tan∠CEO= = =3.
∴CE的长为5,tan∠CEO的值为3.
课堂小结
定义
判定
矩形
性质
第23讲 矩形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第五单元 第23讲
课标要求 作业目标
矩形 1.理解矩形的概念. 2.探索并证明矩形的性质定理:矩形的四个角都是直角,对角线相等. 3.探索并证明矩形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形. 掌握矩形的概念及性质定理,并能运用它们解决几何证明问题和生活应用问题
掌握直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”,并能运用它解决几何证明问题和简单的实际问题
掌握矩形的判定定理,并能运用它们解决几何证明问题和简单的实际问题
会分析矩形和平行四边形之间的区别和联系,进一步认识一般与特殊的关系
在综合的实际问题情境中抽象出数学模型,建立形数之间的联系
要求与目标
教材整合 核心归纳
02
第五单元 第23讲
2. 操作1:同P87操作1,如图①,两个三角形满足形状
为 三角形,即∠B=∠D= °,则四边形
ABCD为矩形;操作2:同P87操作2,如图②,两根木棒满足
条件AC BD,则四边形ABCD为矩形.
48
直角
90
=
第2题图
1. 已知矩形的一边长为6cm,一条对角线的长为10cm,
则矩形的面积为 cm2.
另一边长为 =8
矩形四个角都是直角;
对角线相等
定义 平行四边形 矩形
性质 特殊的平行四边形:矩形具有平行四边形的所有性质;
角:四个角都是直角,即∠ABC=
∠BCD=∠ADC=∠BAD= ;
对角线:对角线互相平分且相等,即AC=BD,
OA=OC= = ;
对称性:既是中心对称图形,又是轴对称图形,有两条对称轴
90°
OB
OD
面积 面积:S= (a,b分别表示矩形的长和宽)
教材典型应用 如右图,已知点P为矩形边AD上任意一点,
PE⊥AC,PF⊥BD,则连接PO,根据面积法可
得出PE+PF是一个定值.见P92T10
ab
考点 矩形的性质【省卷T26,长沙T23】
考点清单
判定 判定方法 几何语言
有一个角是直角的平行四边形 ∵∠CDA= °,
四边形ABCD是平行四边形,
∴四边形ABCD是矩形
对角线相等的平
行四边形 ∵AC BD,
四边形ABCD是平行四边形,
∴四边形ABCD是矩形
有三个角是直角
的四边形 ∵∠CDA=∠DAB=
∠ABC= °,
∴四边形ABCD是矩形
90
=
90
考点 矩形的判定
考点清单
重难精讲
变式探究
03
第五单元 第23讲
例 改编问题链如下图, ABCD的对角线AC,BD相交于点O,已知AB=4.
(1)若△AOB是等边三角形.
①求证: ABCD是矩形;②求AD的长;
①证明:∵△AOB为等边三角形,∴OA=OB.
∵四边形ABCD是平行四边形,
∴OB=OD= BD,OA=OC= AC.
∴BD=AC. ∴ ABCD是矩形.
②解:∵ ABCD是矩形,∴∠BAD=90°.
∵△AOB为等边三角形,
∴∠ABO=60°.∴∠ADB=90°-60°=30°.
∴AD= AB=4 .
OA=OB
AC=BD
AD=ABtan60°
(2)【逆向设问】若∠BAD=90°,∠ABD=60°,求△AOB
的周长.
例 改编问题链如下图, ABCD的对角线AC,BD相交于点O,
已知AB=4.
解:∵四边形ABCD是平行四边形,
∠BAD=90°,
∴ ABCD是矩形.∴AC=BD. ∴OB=
BD= AC=OA.
又∵∠ABO=60°,∴△AOB为等边三角形.
∴△AOB的周长为12.
ABCD是矩形
OA=OB
△AOB为等边三角形
△AOB的
周长为12
1. (2024·成都)如下图,在矩形ABCD中,对角线AC与BD相交
于点O,则下列结论一定正确的是( C )
A. AB=AD
B. AC⊥BD
C. AC=BD
D. ∠ACB=∠ACD
第1题图
C
2. (2024·吉林)如下图,在平面直角坐标系中,点A的坐标为
(-4,0),点C的坐标为(0,2).以OA,OC为边作矩形OABC.
若将矩形OABC绕点O顺时针旋转90°,得到矩形OA'B'C',
则点B'的坐标为( C )
A. (-4,-2) B. (-4,2)
C. (2,4) D. (4,2)
第2题图
C
(-4,2)
-4
2
(2,4)
3. (2023·湘西州)如图,在矩形ABCD中,点E在边BC上,点F是AE的中点,AB=8,AD=DE=10,
则BF的长为 .
2
8
10
10
10
6
8
4
BF=AE
在Rt△DEC 中
EC==6
BE=4
在Rt△ABE中,
AE==4
BF=2
4. 如下图,将矩形ABCD沿对角线AC折叠,点B的对应点为
点E,AE与CD交于点F. 求证:△DAF≌△ECF.
第4题图
证明:将矩形ABCD沿对角线AC折叠,
则AD=BC=EC,
∠D=∠B=∠E=90°.
在△DAF和△ECF中,
∴△DAF≌△ECF(AAS).
5. 要检验一个四边形的桌面是否为矩形,可行的测量方案是
( C )
A. 测量两条对角线是否相等
B. 度量两个角是否是90°
C. 测量两条对角线的交点到四个顶点的距离是否相等
D. 测量两组对边是否分别相等
C
6. (2023·岳阳)如下图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
第6题图
(1)你添加的条件是 (填序号);
①(或②)
(2)添加条件后,请证明 ABCD为矩形.
添加条件①.
添加条件①.
证明:∵四边形ABCD是平行四边形,
∴∠A+∠D=180°.
在△ABM和DCM中,
∴△ABM≌△DCM(SAS).
∴∠A=∠D. ∴∠A=∠D=90°.
∴ ABCD为矩形.(选②证明也可)
易得△ABM≌△DCM(SAS)
∠A=∠D=90°
∠A+∠D=180°
AB=DC
∴AB∥DC,AB=DC.
ABCD为矩形
易得△ABM≌△DCM(SSS)
7. (2024·兰州)如下图,在△ABC中,AB=AC,点D是BC的中点,
CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE是矩形;
第7题图
证明:∵在△ABC中,AB=AC,点D是BC的中点,
∴AD⊥BC,
即∠ADC=∠ADB=90°.
∵CE∥AD,
∴∠ECD=∠ADB=90°.
∵AE⊥AD,
∴∠EAD=90°.
∴∠ADC=∠ECD=∠EAD=90°.
∴四边形ADCE是矩形.
三线合一
∠ADB=∠ADC=90°
∠ECD=∠ADB=90°
∠EAD=90°
四边形ADCE是矩形
(2)若BC=4,CE=3,求EF的长.
7. (2024·兰州)如下图,在△ABC中,AB=AC,点D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
解:∵在△ABC中,AB=AC,点D是BC的中点,BC=4,
∴BD=CD= BC=2.
由(1)可知四边形ADCE是矩形,
∴AE=CD=2,∠AEC=90°.
在Rt△AEC中,AE=2,CE=3,
由勾股定理得AC= = .
∵EF⊥AC,由三角形的面积公式得
S△AEC= AC·EF= AE·CE,
∴EF= = = .
3
3
2
2
面积法
S△AEC= AC·EF= AE·CE
2
由勾股定理得AC =
EF=
8. 如下图,矩形ABCD中,AB=2,点E是AC的中点,
∠AED=120°,则AD的长为( A )
A. 2 B. 4 C. 3 D. 5
第8题图
A
9. 矩形ABCD的对角线AC,BD相交于点O,点F在矩形
ABCD的边上,连接OF. 若∠ADB=38°,∠BOF=30°,
则∠AOF的度数为 .
10. 【面积法】如图,在矩形ABCD中,已知AD=12,
AB=5,点P是AD边上任意一点,PE⊥AC,PF⊥BD,点E,
F分别是垂足,则PE+PF的长为 .
46°或106°
第10题图
11. (2024·长沙)如下图,在 ABCD中,对角线AC,BD相交
于点O,∠ABC=90°.
(1)求证:AC=BD;
(1)证明:∵四边形ABCD是平行四边形,
∠ABC=90°,
∴四边形ABCD是矩形.
∴AC=BD.
证明:∵四边形ABCD是平行四边形,
∠ABC=90°,
∴四边形ABCD是矩形.
∴AC=BD.
解:如图,作OH⊥BC于点H,则∠OHE=∠OHC=90°.
∵∠ABC=90°,AB=6,BC=8,
∴AC= = =10.
∴OC=OA= AC=5.
∵∠CEO=∠COE,∴CE=OC=5.
∵OC=OA= AC,OB=OD= BD,且AC=BD,∴OC=OB.
∴HC=HB= BC=4.
∴EH=CE-HC=5-4=1.
∵ = =tan∠ACB,
11. (2024·长沙)如下图,在 ABCD中,对角线AC,BD相交于点O,∠ABC=90°.
(2)点E在BC边上,满足∠CEO=∠COE. 若AB=6,BC=8,
求CE的长及tan∠CEO的值.
∴OH= ·HC= ×4=3.
∴tan∠CEO= = =3.
∴CE的长为5,tan∠CEO的值为3.
课堂小结
定义
判定
矩形
性质
同课章节目录
