第24讲 菱形 2025年中考一轮数学专题复习课件(湖南)(共20张PPT)
文档属性
| 名称 | 第24讲 菱形 2025年中考一轮数学专题复习课件(湖南)(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 988.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:27:35 | ||
图片预览







文档简介
(共20张PPT)
第24讲 菱形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第五单元 第24讲
课标要求 作业目标
菱形 1.理解菱形的概念. 2.探索并证明菱形的性质定理:菱形的四条边相等,对角线互相垂直. 3.探索并证明菱形的判定定理:四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形. 掌握菱形的概念、性质以及判定定理,并能运用它们解决几何证明问题和生活应用问题
会分析菱形和平行四边形之间的区别和联系,进一步认识一般与特殊的关系
在综合的实际问题情境中抽象出数学模型,建立形数之间的联系
要求与目标
教材整合 核心归纳
02
第五单元 第24讲
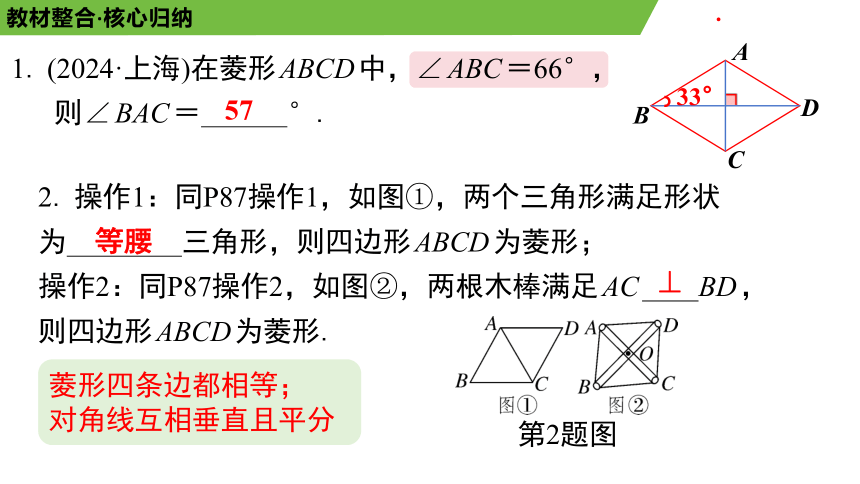
1. (2024·上海)在菱形ABCD中,∠ABC=66°,
则∠BAC= °.
第2题图
57
2. 操作1:同P87操作1,如图①,两个三角形满足形状
为 三角形,则四边形ABCD为菱形;
操作2:同P87操作2,如图②,两根木棒满足AC BD,
则四边形ABCD为菱形.
等腰
⊥
A
B
C
D
33°
菱形四条边都相等;
对角线互相垂直且平分
定
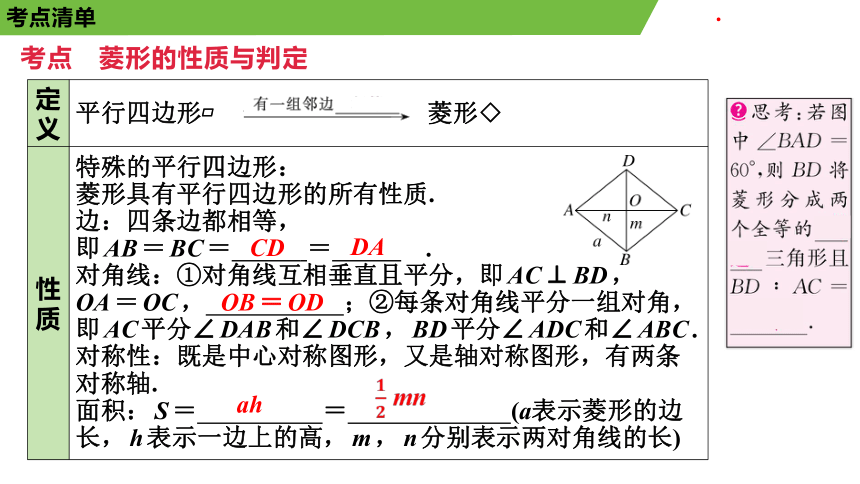
义 平行四边形 菱形◇
性
质 特殊的平行四边形:
菱形具有平行四边形的所有性质.
边:四条边都相等,
即AB=BC= .= .
对角线:①对角线互相垂直且平分,即AC⊥BD,
OA=OC, ;②每条对角线平分一组对角,即AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.
对称性:既是中心对称图形,又是轴对称图形,有两条对称轴.
面积:S= = (a表示菱形的边长,h表示一边上的高,m,n分别表示两对角线的长)
CD
DA
OB=OD
ah
mn
考点 菱形的性质与判定
考点清单
判
定 判定方法 几何语言
有一组邻边相等的平行四边形(定义) ∵AD= ,
四边形ABCD是平行四边形,
∴四边形ABCD是菱形
对角线互相垂直的平行四边形 ∵AC BD,四边形ABCD是平行四边形,∴四边形ABCD是菱形
四条边相等的四边形 ∵AB= = = ,
∴四边形ABCD是菱形
AB(或CD)
⊥
BC
CD
AD
重难精讲
变式探究
03
第五单元 第24讲
例 如下图,四边形ABCD是菱形,点E,F是对角线AC上的两点,且AE=CF,连接BF,FD,DE,EB. 求证:四边形DEBF是菱形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠DAB=∠DCB,
AC平分∠DAB,CA平分∠DCB.
∴∠DAC=∠BAC= ∠DAB,
∠DCA=∠ACB= ∠DCB.
∴∠DAC=∠BAC=∠DCA=∠ACB.
∵AE=CF,
∴△DAE≌△BAE≌△BCF≌△DCF(SAS).
∴DE=BE=BF=DF.
∴四边形DEBF是菱形.
AB=BC=CD=AD
易得∠DAC=∠BAC=∠DCA=∠ACB
△DAE≌△BAE≌△BCF≌△DCF(SAS)
DE=BE=BF=DF
四边形DEBF是菱形
1. 如下图, ABCD的对角线AC和BD相交于点O,下列条件
能判定 ABCD是菱形的是( D )
A. OB=OD B. AC=BD
C. OA=OD D. AC⊥BD
第1题图
D
2. (2024·武汉)如图,小美同学按如下步骤作四边形ABCD:
(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别
交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位
长为半径画弧,两弧交于点C;(4)连接BC,CD,BD. 若
∠A=44°,则∠CBD的大小是( C )
A. 64° B. 66°
C. 68° D. 70°
第2题图
C
3. (2024·临夏州)如下图,点O是坐标原点,菱形ABOC的顶点
B在x轴的负半轴上,顶点C的坐标为(3,4),则顶点A的坐标
为( C )
A. (-4,2)
B. (- ,4)
C. (-2,4)
D. (-4, )
C
4
E
3
4
F
5
3
由勾股定理得OC=5
AB=OC=BO=5
AB∥OC
∠ABO=∠COE
易证△ABF≌△COE
BF=OE=3
OF=BO-BE=5-3=2
4. (2022·长沙)如下图,在 ABCD中,对角线AC,BD相交于
点O,AB=AD.
(1)求证:AC⊥BD;
证明:∵四边形ABCD是平行四边形,
AB=AD,
∴ ABCD是菱形.
∴AC⊥BD.
(2)若点E,F分别为AD,AO的中点,连接EF,EF= ,
AO=2,求BD的长及四边形ABCD的周长.
中位线
OD=2EF=3
BD=2OD=6
3
2
=
C菱形ABCD=4AD=4
(2)若点E,F分别为AD,AO的中点,连接EF,EF= ,
AO=2,求BD的长及四边形ABCD的周长.
第4题图
解:∵点E,F分别为AD,AO的中点,
∴EF是△AOD的中位线.
∴OD=2EF=3.
由(1)可知四边形ABCD是菱形,
∴AB=BC=CD=AD,BD=2OD=6.
在Rt△AOD中,由勾股定理得
AD= = = ,
∴C菱形ABCD=4AD=4 .
4. (2022·长沙)如下图,在 ABCD中,对角线AC,BD相交于
点O,AB=AD.
5. 【面积法】(2024·绥化)如下图,四边形ABCD是菱形,
CD=5,BD=8,AE⊥CD于点E,则AE的长是( A )
A. B. 6 C. D. 12
第5题图
A
6. 如图,矩形ABCD的对角线AC,BD相交于点O,
DE∥AC,CE∥BD. 若AC=10,则四边形OCED的周长
是 .
第6题图
20
7. 如下图,矩形纸片ABCD中,G,F分别是边BC,AD上的
点,将纸片沿GF折叠,使顶点B落在边AD上的点E处.
(1)求证:四边形BGEF为菱形;
证明:由图形的折叠可知BG=EG,
AB=EH,∠BGF=∠EGF.
∵EF∥BG,
∴∠BGF=∠EFG.
∴∠EGF=∠EFG. ∴EF=EG. ∴BG=EF.
∴四边形BGEF为平行四边形.
又∵EF=EG,∴四边形BGEF为菱形.
(2)若AB=8,BG=10,求折痕GF的长.
解:如图,连接BE,与FG交于点O.
由(1)知四边形BGEF为菱形,
∴BE,FG互相垂直平分.
在Rt△EFH中,EF=BG=10,EH=AB=8.
∴FH=AF=6.∴AE=AF+EF=16.
∴BE= =8 .∴BO=4 .
∴OG= =2 .
∵四边形BGEF是菱形,
∴GF=2OG=4 .
7. 如下图,矩形纸片ABCD中,G,F分别是边BC,AD上的
点,将纸片沿GF折叠,使顶点B落在边AD上的点E处.
课堂小结
定义
判定
菱形
性质
第24讲 菱形
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第五单元 第24讲
课标要求 作业目标
菱形 1.理解菱形的概念. 2.探索并证明菱形的性质定理:菱形的四条边相等,对角线互相垂直. 3.探索并证明菱形的判定定理:四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形. 掌握菱形的概念、性质以及判定定理,并能运用它们解决几何证明问题和生活应用问题
会分析菱形和平行四边形之间的区别和联系,进一步认识一般与特殊的关系
在综合的实际问题情境中抽象出数学模型,建立形数之间的联系
要求与目标
教材整合 核心归纳
02
第五单元 第24讲
1. (2024·上海)在菱形ABCD中,∠ABC=66°,
则∠BAC= °.
第2题图
57
2. 操作1:同P87操作1,如图①,两个三角形满足形状
为 三角形,则四边形ABCD为菱形;
操作2:同P87操作2,如图②,两根木棒满足AC BD,
则四边形ABCD为菱形.
等腰
⊥
A
B
C
D
33°
菱形四条边都相等;
对角线互相垂直且平分
定
义 平行四边形 菱形◇
性
质 特殊的平行四边形:
菱形具有平行四边形的所有性质.
边:四条边都相等,
即AB=BC= .= .
对角线:①对角线互相垂直且平分,即AC⊥BD,
OA=OC, ;②每条对角线平分一组对角,即AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.
对称性:既是中心对称图形,又是轴对称图形,有两条对称轴.
面积:S= = (a表示菱形的边长,h表示一边上的高,m,n分别表示两对角线的长)
CD
DA
OB=OD
ah
mn
考点 菱形的性质与判定
考点清单
判
定 判定方法 几何语言
有一组邻边相等的平行四边形(定义) ∵AD= ,
四边形ABCD是平行四边形,
∴四边形ABCD是菱形
对角线互相垂直的平行四边形 ∵AC BD,四边形ABCD是平行四边形,∴四边形ABCD是菱形
四条边相等的四边形 ∵AB= = = ,
∴四边形ABCD是菱形
AB(或CD)
⊥
BC
CD
AD
重难精讲
变式探究
03
第五单元 第24讲
例 如下图,四边形ABCD是菱形,点E,F是对角线AC上的两点,且AE=CF,连接BF,FD,DE,EB. 求证:四边形DEBF是菱形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠DAB=∠DCB,
AC平分∠DAB,CA平分∠DCB.
∴∠DAC=∠BAC= ∠DAB,
∠DCA=∠ACB= ∠DCB.
∴∠DAC=∠BAC=∠DCA=∠ACB.
∵AE=CF,
∴△DAE≌△BAE≌△BCF≌△DCF(SAS).
∴DE=BE=BF=DF.
∴四边形DEBF是菱形.
AB=BC=CD=AD
易得∠DAC=∠BAC=∠DCA=∠ACB
△DAE≌△BAE≌△BCF≌△DCF(SAS)
DE=BE=BF=DF
四边形DEBF是菱形
1. 如下图, ABCD的对角线AC和BD相交于点O,下列条件
能判定 ABCD是菱形的是( D )
A. OB=OD B. AC=BD
C. OA=OD D. AC⊥BD
第1题图
D
2. (2024·武汉)如图,小美同学按如下步骤作四边形ABCD:
(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别
交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位
长为半径画弧,两弧交于点C;(4)连接BC,CD,BD. 若
∠A=44°,则∠CBD的大小是( C )
A. 64° B. 66°
C. 68° D. 70°
第2题图
C
3. (2024·临夏州)如下图,点O是坐标原点,菱形ABOC的顶点
B在x轴的负半轴上,顶点C的坐标为(3,4),则顶点A的坐标
为( C )
A. (-4,2)
B. (- ,4)
C. (-2,4)
D. (-4, )
C
4
E
3
4
F
5
3
由勾股定理得OC=5
AB=OC=BO=5
AB∥OC
∠ABO=∠COE
易证△ABF≌△COE
BF=OE=3
OF=BO-BE=5-3=2
4. (2022·长沙)如下图,在 ABCD中,对角线AC,BD相交于
点O,AB=AD.
(1)求证:AC⊥BD;
证明:∵四边形ABCD是平行四边形,
AB=AD,
∴ ABCD是菱形.
∴AC⊥BD.
(2)若点E,F分别为AD,AO的中点,连接EF,EF= ,
AO=2,求BD的长及四边形ABCD的周长.
中位线
OD=2EF=3
BD=2OD=6
3
2
=
C菱形ABCD=4AD=4
(2)若点E,F分别为AD,AO的中点,连接EF,EF= ,
AO=2,求BD的长及四边形ABCD的周长.
第4题图
解:∵点E,F分别为AD,AO的中点,
∴EF是△AOD的中位线.
∴OD=2EF=3.
由(1)可知四边形ABCD是菱形,
∴AB=BC=CD=AD,BD=2OD=6.
在Rt△AOD中,由勾股定理得
AD= = = ,
∴C菱形ABCD=4AD=4 .
4. (2022·长沙)如下图,在 ABCD中,对角线AC,BD相交于
点O,AB=AD.
5. 【面积法】(2024·绥化)如下图,四边形ABCD是菱形,
CD=5,BD=8,AE⊥CD于点E,则AE的长是( A )
A. B. 6 C. D. 12
第5题图
A
6. 如图,矩形ABCD的对角线AC,BD相交于点O,
DE∥AC,CE∥BD. 若AC=10,则四边形OCED的周长
是 .
第6题图
20
7. 如下图,矩形纸片ABCD中,G,F分别是边BC,AD上的
点,将纸片沿GF折叠,使顶点B落在边AD上的点E处.
(1)求证:四边形BGEF为菱形;
证明:由图形的折叠可知BG=EG,
AB=EH,∠BGF=∠EGF.
∵EF∥BG,
∴∠BGF=∠EFG.
∴∠EGF=∠EFG. ∴EF=EG. ∴BG=EF.
∴四边形BGEF为平行四边形.
又∵EF=EG,∴四边形BGEF为菱形.
(2)若AB=8,BG=10,求折痕GF的长.
解:如图,连接BE,与FG交于点O.
由(1)知四边形BGEF为菱形,
∴BE,FG互相垂直平分.
在Rt△EFH中,EF=BG=10,EH=AB=8.
∴FH=AF=6.∴AE=AF+EF=16.
∴BE= =8 .∴BO=4 .
∴OG= =2 .
∵四边形BGEF是菱形,
∴GF=2OG=4 .
7. 如下图,矩形纸片ABCD中,G,F分别是边BC,AD上的
点,将纸片沿GF折叠,使顶点B落在边AD上的点E处.
课堂小结
定义
判定
菱形
性质
同课章节目录
