第27讲 与圆有关的位置关系 2025年中考一轮数学专题复习课件(湖南)(共24张PPT)
文档属性
| 名称 | 第27讲 与圆有关的位置关系 2025年中考一轮数学专题复习课件(湖南)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:30:47 | ||
图片预览








文档简介
(共24张PPT)
第27讲 与圆有关的位置关系
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第六单元 第27讲
课标要求 作业目标
与圆有关的位置关系 了解点和圆、直线和圆的位置关系. 掌握点和圆的位置关系
了解直线和圆的位置关系,掌握切线的概念、切线的判定定理及性质定理。会用尺规作图:过圆外一点作圆的切线.理解切线长定理
了解三角形的内心和外心,会利用基本作图作三角形的外接圆、内切圆.
要求与目标
教材整合 核心归纳
02
第六单元 第27讲
1. 点P为☉O外一点,PA,PB分别切☉O于A,B两点,
若PA=6,则PB= .
2. 平面直角坐标系中,☉P的圆心坐标为(-4,-5),
半径为 5,那么☉P与y轴的位置关系是 .
3. 如右图,AB为☉O的切线,A为切点,
BO交☉O于点C,点D在☉O上.若∠ABO=32°,
则∠ADC= °.
6
相交
29
第3题图
从圆外一点可以引圆的两条切线,它们的切线长相等
O
x
y
P
5
4
∠BAO=90°
∠O=58°
∠D=∠O=29°
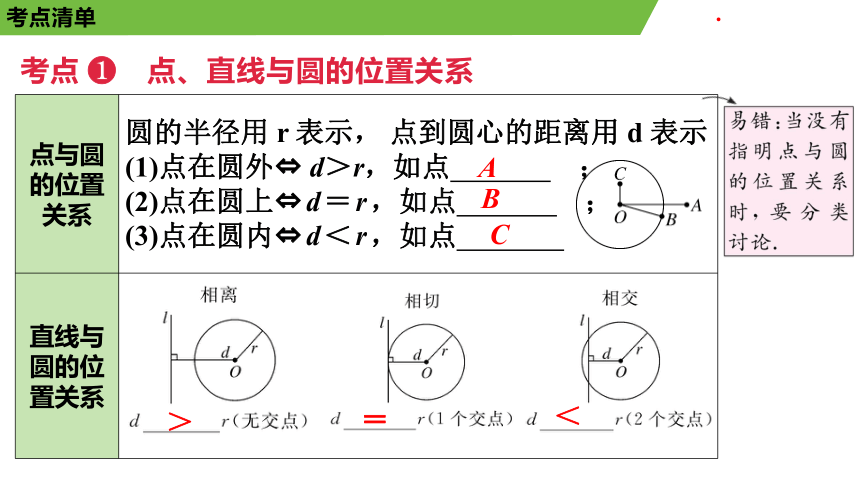
点与圆的位置关系 圆的半径用 r 表示, 点到圆心的距离用 d 表示
(1)点在圆外 d>r,如点 ;
(2)点在圆上 d=r,如点 ;
(3)点在圆内 d<r,如点
直线与圆的位置关系
A
B
C
=
<
>
考点 点、直线与圆的位置关系
考点清单
性质 圆的切线垂直于过切点的半径.即 PA 是圆 O 的切线,
则 OA⊥PA
判定 (1)和圆只有一个公共点的直线是圆的切线(定义法);
(2)经过半径的外端并且垂直于这条半径的直线是圆的切线;
(3)圆心到已知直线的距离等于半径长,则这条直线是圆的切线
考点 圆的切线【省卷T26】
切线长定理 从圆外一点可以引圆的两条切线,它们的切线
长 ,这一点和圆心的连线 两条切线的夹角.如左图,有PA= ,且∠APO=
相等
平分
PB
∠BPO
考点清单
圆心名称 性质
外接圆 外心:三角形外接圆圆心,是三角形三边 的 的交点 (1)三角形的外心到三角形的三个顶点的距离相等.如左图,有OA= =OC;
(2)外心不一定在三角形的内部;
(3)∠BOC=2
内切圆 内心:三角形内切圆圆心,是三角形三条 的交点 (1)三角形的内心到三角形三条边的 相等.如左图,有OE= =OD;
(2)内心在三角形内部
垂直平分线
OB
∠BAC
角平分线
距离
OF
内切圆 教材典型应用:△ABC的三边长BC,AC,AB的
长分别为a,b,c,则
(1)∠BOC=90°+ ∠BAC;
(2)S△ABC=S△AOB+S△AOC+S△BOC= r(a+b+c);
(3)△ABC中,若∠ACB=90°,则内切圆半径r=
考点 三角形的外接圆与内切圆【长沙T24】
考点清单
重难精讲
变式探究
03
第六单元 第27讲
例1 【有切点,连半径,证垂直】如下图,在△ABC中,
AB=AC,∠BAC=120°,点D在BC边上,☉D经过点A和点B且与BC边相交于点E.
(1)求证:AC是☉D的切线;
例1题图
证明:如图,连接AD. ∵AB=AC,
∠BAC=120°,∴∠B=∠C=30°.
∵AD=BD,∴∠BAD=∠B=30°.
∴∠ADC=60°.
∴∠DAC=180°-60°-30°=90°.
∵AD为☉D的半径,∴AC是☉D的切线.
连接AD,求证∠DAC=90°
∠B=∠C=30°
AD=BD
∠B=∠BAD=30°
∠DAC=90°
2
60°
例1 【有切点,连半径,证垂直】如下图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上,☉D经过点A和点B且与BC边相交于点E.
(2)若CE=2 ,求☉D的半径.
解:如图,连接AE. ∵AD=DE,
∠ADE=60°,∴△ADE是等边三角形.
∴AD=AE=DE,∠AED=60°.
∴∠EAC=∠AED-∠C=30°.
∴∠EAC=∠C. ∴AE=CE=2 .
∴☉D的半径为2 .
AD=DE,∠ADE=60°
△ADE是等边三角形
∠AED=60°
∠EAC=∠C=30°
DE=AE=CE=2
例2 【无切点,作垂直,证半径】如图,
△ABC为等腰三角形,AB=AC,点O是底边BC的中点,
☉O与腰AB相切于点D. 求证:AC与☉O相切.
证明:如图,连接OD,
过点O作OE⊥AC于点E.
∵AB切☉O于点D,∴OD⊥AB.
∴∠ODB=∠OEC=90°.
∵O是BC的中点,∴OB=OC.
∵AB=AC,∴∠B=∠C.
在△OBD和△OCE中,
∴△OBD≌△OCE(AAS).
∴OE=OD,即OE是☉O的半径.∴AC与☉O相切.
E
连接OD,过点O作
OE⊥AC于点E
∠B=∠C
OB=OC
∠ODB=∠OEC=90°
△OBD≌△OCE(AAS)
OD=OE
AC与☉O相切
【逆向变式】如图,△ABC的两边分别与☉O相切于点D和E,其中圆心O为BC的中点,
求证:△ABC为等腰三角形.
证明:如图,连接OD,OE.
∵△ABC的两边分别与☉O相切于点D和E,
∴∠BDO=∠CEO=90°.
∵圆心O为BC的中点,∴OB=OC.
在Rt△OBD和Rt△OCE中,
∴Rt△OBD≌Rt△OCE(HL).
∴∠B=∠C. ∴AB=AC.
∴△ABC为等腰三角形.
E
连接OD,OE,
∠BDO=∠CEO=90°,
DO=OE
OB=OC
Rt△OBD≌Rt△OCE(HL)
∠B=∠C
AB=AC
△ABC为等腰三角形
1. (2024·广州)如下图,☉O中,弦AB的长为4 ,点C在
☉O上,OC⊥AB,∠ABC=30°.☉O所在的平面内有一点
P,若OP=5,则点P与☉O的位置关系是( C )
A. 点P在☉O上 B. 点P在☉O内
C. 点P在☉O外 D. 无法确定
第1题图
C
2. 如图,在△ABC中,∠ACB=90°,AB=5,BC=4.以
点A为圆心,r为半径作圆,当点C在☉A内且点B在☉A外
时,r的值可能是( C )
A. 2 B. 3 C. 4 D. 5
第2题图
C
4
5
在Rt△ABC中,AC=3
3<r<5
3
3. 如下图,PA,PB分别与☉O相切于A,B两点,连接
AO,BO. 若∠APB=70°,则∠AOP的度数为 °.
第3题图
55
4. (2024·山西)如图,已知△ABC,以AB为直径的☉O交BC
于点D,与AC相切于点A,连接OD. 若∠AOD=80°,则
∠C的度数为 °.
第4题图
50
∠BAC=90°
∠B=∠AOD=40°
∠C=50°
5. 如图,点O是△ABC外接圆的圆心,AI平分∠BAC,
连接OB,OC. 若∠CAI=35°,
则∠OBC的度数为( C )
A. 15° B. 17.5°
C. 20° D. 25°
第5题图
C
6. 如图,正方形ABCD的外接圆的半径为4,
则它的内切圆的半径为 .
2
第6题图
7. (2024·自贡节选)在Rt△ABC中,∠C=90°,☉O是△ABC
的内切圆,切点分别为点D,E,F. 图中三组相等的线段
分别是CE=CF,AF= ,BD= ;
若AC=3,BC=4,则☉O的半径长为 .
AD
BE
1
从圆外一点引圆的两条切线,
它们的切线长相等
令☉O的半径长为 r
r
r
r
AB=5
3-r
4-r
4-r
3-r
4-r+3-r=5
r=1
8. 如图,正方形的两边与☉O相切,对角线AB与☉O相交
于点M,N(点N在点M的右上方),若AB的长度为10,☉O的
半径为2,则BN的长度为 .
第8题图
8-2
9. (2023·益阳节选)如下图,线段AB与☉O相切于点B,AO交
☉O于点M,其延长线交☉O于点C,连接BC,∠ABC=
120°,D为☉O上一点且 的中点为M,连接AD,CD.
(1)求∠ACB的度数;
解:(1)如图,连接OB.
∵线段AB与☉O相
切于点B,
∴∠OBA=90°.
∴∠OBC=120°-90°=30°.
∵OB=OC,∴∠ACB=∠OBC=30°.
解:如图,连接OB.
∵线段AB与☉O相切于点B,
∴∠OBA=90°.
∴∠OBC=120°-90°=30°.
∵OB=OC,∴∠ACB=∠OBC=30°.
(2)四边形ABCD是否是菱形?如果是,请证明;如果不是,请说明理由.
解:四边形ABCD为菱形.
证明如下:如图,连接DM,BM.
∵M是 的中点,
∴DM=BM,∠DCM=∠BCM=30°.
∴∠DMA=∠BMA=30°+90°=120°.
∴△ADM≌△ABM(SAS).
∴AD=AB,∠DAM=∠BAM=180°-120°-30°=30°.
∴∠DAC=∠DCA,∠BAC=∠BCA.
∴AD=CD,AB=BC.
∴AB=BC=CD=AD.
∴四边形ABCD为菱形.
9. (2023·益阳节选)如下图,线段AB与☉O相切于点B,AO交☉O于点M,其延长线交☉O于点C,连接BC,∠ABC=120°,D为☉O上一点且 的中点为M,连接AD,CD.
课堂小结
与圆有关的位置关系
点与圆、直线与圆的位置关系
切线的性质与判定
三角形的外接圆和内切圆
第27讲 与圆有关的位置关系
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第六单元 第27讲
课标要求 作业目标
与圆有关的位置关系 了解点和圆、直线和圆的位置关系. 掌握点和圆的位置关系
了解直线和圆的位置关系,掌握切线的概念、切线的判定定理及性质定理。会用尺规作图:过圆外一点作圆的切线.理解切线长定理
了解三角形的内心和外心,会利用基本作图作三角形的外接圆、内切圆.
要求与目标
教材整合 核心归纳
02
第六单元 第27讲
1. 点P为☉O外一点,PA,PB分别切☉O于A,B两点,
若PA=6,则PB= .
2. 平面直角坐标系中,☉P的圆心坐标为(-4,-5),
半径为 5,那么☉P与y轴的位置关系是 .
3. 如右图,AB为☉O的切线,A为切点,
BO交☉O于点C,点D在☉O上.若∠ABO=32°,
则∠ADC= °.
6
相交
29
第3题图
从圆外一点可以引圆的两条切线,它们的切线长相等
O
x
y
P
5
4
∠BAO=90°
∠O=58°
∠D=∠O=29°
点与圆的位置关系 圆的半径用 r 表示, 点到圆心的距离用 d 表示
(1)点在圆外 d>r,如点 ;
(2)点在圆上 d=r,如点 ;
(3)点在圆内 d<r,如点
直线与圆的位置关系
A
B
C
=
<
>
考点 点、直线与圆的位置关系
考点清单
性质 圆的切线垂直于过切点的半径.即 PA 是圆 O 的切线,
则 OA⊥PA
判定 (1)和圆只有一个公共点的直线是圆的切线(定义法);
(2)经过半径的外端并且垂直于这条半径的直线是圆的切线;
(3)圆心到已知直线的距离等于半径长,则这条直线是圆的切线
考点 圆的切线【省卷T26】
切线长定理 从圆外一点可以引圆的两条切线,它们的切线
长 ,这一点和圆心的连线 两条切线的夹角.如左图,有PA= ,且∠APO=
相等
平分
PB
∠BPO
考点清单
圆心名称 性质
外接圆 外心:三角形外接圆圆心,是三角形三边 的 的交点 (1)三角形的外心到三角形的三个顶点的距离相等.如左图,有OA= =OC;
(2)外心不一定在三角形的内部;
(3)∠BOC=2
内切圆 内心:三角形内切圆圆心,是三角形三条 的交点 (1)三角形的内心到三角形三条边的 相等.如左图,有OE= =OD;
(2)内心在三角形内部
垂直平分线
OB
∠BAC
角平分线
距离
OF
内切圆 教材典型应用:△ABC的三边长BC,AC,AB的
长分别为a,b,c,则
(1)∠BOC=90°+ ∠BAC;
(2)S△ABC=S△AOB+S△AOC+S△BOC= r(a+b+c);
(3)△ABC中,若∠ACB=90°,则内切圆半径r=
考点 三角形的外接圆与内切圆【长沙T24】
考点清单
重难精讲
变式探究
03
第六单元 第27讲
例1 【有切点,连半径,证垂直】如下图,在△ABC中,
AB=AC,∠BAC=120°,点D在BC边上,☉D经过点A和点B且与BC边相交于点E.
(1)求证:AC是☉D的切线;
例1题图
证明:如图,连接AD. ∵AB=AC,
∠BAC=120°,∴∠B=∠C=30°.
∵AD=BD,∴∠BAD=∠B=30°.
∴∠ADC=60°.
∴∠DAC=180°-60°-30°=90°.
∵AD为☉D的半径,∴AC是☉D的切线.
连接AD,求证∠DAC=90°
∠B=∠C=30°
AD=BD
∠B=∠BAD=30°
∠DAC=90°
2
60°
例1 【有切点,连半径,证垂直】如下图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上,☉D经过点A和点B且与BC边相交于点E.
(2)若CE=2 ,求☉D的半径.
解:如图,连接AE. ∵AD=DE,
∠ADE=60°,∴△ADE是等边三角形.
∴AD=AE=DE,∠AED=60°.
∴∠EAC=∠AED-∠C=30°.
∴∠EAC=∠C. ∴AE=CE=2 .
∴☉D的半径为2 .
AD=DE,∠ADE=60°
△ADE是等边三角形
∠AED=60°
∠EAC=∠C=30°
DE=AE=CE=2
例2 【无切点,作垂直,证半径】如图,
△ABC为等腰三角形,AB=AC,点O是底边BC的中点,
☉O与腰AB相切于点D. 求证:AC与☉O相切.
证明:如图,连接OD,
过点O作OE⊥AC于点E.
∵AB切☉O于点D,∴OD⊥AB.
∴∠ODB=∠OEC=90°.
∵O是BC的中点,∴OB=OC.
∵AB=AC,∴∠B=∠C.
在△OBD和△OCE中,
∴△OBD≌△OCE(AAS).
∴OE=OD,即OE是☉O的半径.∴AC与☉O相切.
E
连接OD,过点O作
OE⊥AC于点E
∠B=∠C
OB=OC
∠ODB=∠OEC=90°
△OBD≌△OCE(AAS)
OD=OE
AC与☉O相切
【逆向变式】如图,△ABC的两边分别与☉O相切于点D和E,其中圆心O为BC的中点,
求证:△ABC为等腰三角形.
证明:如图,连接OD,OE.
∵△ABC的两边分别与☉O相切于点D和E,
∴∠BDO=∠CEO=90°.
∵圆心O为BC的中点,∴OB=OC.
在Rt△OBD和Rt△OCE中,
∴Rt△OBD≌Rt△OCE(HL).
∴∠B=∠C. ∴AB=AC.
∴△ABC为等腰三角形.
E
连接OD,OE,
∠BDO=∠CEO=90°,
DO=OE
OB=OC
Rt△OBD≌Rt△OCE(HL)
∠B=∠C
AB=AC
△ABC为等腰三角形
1. (2024·广州)如下图,☉O中,弦AB的长为4 ,点C在
☉O上,OC⊥AB,∠ABC=30°.☉O所在的平面内有一点
P,若OP=5,则点P与☉O的位置关系是( C )
A. 点P在☉O上 B. 点P在☉O内
C. 点P在☉O外 D. 无法确定
第1题图
C
2. 如图,在△ABC中,∠ACB=90°,AB=5,BC=4.以
点A为圆心,r为半径作圆,当点C在☉A内且点B在☉A外
时,r的值可能是( C )
A. 2 B. 3 C. 4 D. 5
第2题图
C
4
5
在Rt△ABC中,AC=3
3<r<5
3
3. 如下图,PA,PB分别与☉O相切于A,B两点,连接
AO,BO. 若∠APB=70°,则∠AOP的度数为 °.
第3题图
55
4. (2024·山西)如图,已知△ABC,以AB为直径的☉O交BC
于点D,与AC相切于点A,连接OD. 若∠AOD=80°,则
∠C的度数为 °.
第4题图
50
∠BAC=90°
∠B=∠AOD=40°
∠C=50°
5. 如图,点O是△ABC外接圆的圆心,AI平分∠BAC,
连接OB,OC. 若∠CAI=35°,
则∠OBC的度数为( C )
A. 15° B. 17.5°
C. 20° D. 25°
第5题图
C
6. 如图,正方形ABCD的外接圆的半径为4,
则它的内切圆的半径为 .
2
第6题图
7. (2024·自贡节选)在Rt△ABC中,∠C=90°,☉O是△ABC
的内切圆,切点分别为点D,E,F. 图中三组相等的线段
分别是CE=CF,AF= ,BD= ;
若AC=3,BC=4,则☉O的半径长为 .
AD
BE
1
从圆外一点引圆的两条切线,
它们的切线长相等
令☉O的半径长为 r
r
r
r
AB=5
3-r
4-r
4-r
3-r
4-r+3-r=5
r=1
8. 如图,正方形的两边与☉O相切,对角线AB与☉O相交
于点M,N(点N在点M的右上方),若AB的长度为10,☉O的
半径为2,则BN的长度为 .
第8题图
8-2
9. (2023·益阳节选)如下图,线段AB与☉O相切于点B,AO交
☉O于点M,其延长线交☉O于点C,连接BC,∠ABC=
120°,D为☉O上一点且 的中点为M,连接AD,CD.
(1)求∠ACB的度数;
解:(1)如图,连接OB.
∵线段AB与☉O相
切于点B,
∴∠OBA=90°.
∴∠OBC=120°-90°=30°.
∵OB=OC,∴∠ACB=∠OBC=30°.
解:如图,连接OB.
∵线段AB与☉O相切于点B,
∴∠OBA=90°.
∴∠OBC=120°-90°=30°.
∵OB=OC,∴∠ACB=∠OBC=30°.
(2)四边形ABCD是否是菱形?如果是,请证明;如果不是,请说明理由.
解:四边形ABCD为菱形.
证明如下:如图,连接DM,BM.
∵M是 的中点,
∴DM=BM,∠DCM=∠BCM=30°.
∴∠DMA=∠BMA=30°+90°=120°.
∴△ADM≌△ABM(SAS).
∴AD=AB,∠DAM=∠BAM=180°-120°-30°=30°.
∴∠DAC=∠DCA,∠BAC=∠BCA.
∴AD=CD,AB=BC.
∴AB=BC=CD=AD.
∴四边形ABCD为菱形.
9. (2023·益阳节选)如下图,线段AB与☉O相切于点B,AO交☉O于点M,其延长线交☉O于点C,连接BC,∠ABC=120°,D为☉O上一点且 的中点为M,连接AD,CD.
课堂小结
与圆有关的位置关系
点与圆、直线与圆的位置关系
切线的性质与判定
三角形的外接圆和内切圆
同课章节目录
