第28讲 与圆有关的计算 2025年中考一轮数学专题复习课件(湖南)(共17张PPT)
文档属性
| 名称 | 第28讲 与圆有关的计算 2025年中考一轮数学专题复习课件(湖南)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 22:25:55 | ||
图片预览






文档简介
(共17张PPT)
第28讲 与圆有关的计算
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第六单元 第28讲
课标要求 作业目标
与圆有关的计算 掌握与圆相关的计算如弧长、扇形的面积、圆锥侧面积和全面积. 掌握弧长和扇形面积的公式,并会用其计算弧长和扇形面积,会利用弧长、扇形面积计算公式计算简单组合图形的周长和面积
知道圆锥的侧面展开图是扇形,了解圆锥各部分名称.会计算圆锥的侧面积和全面积
要求与目标
教材整合 核心归纳
02
第六单元 第28讲
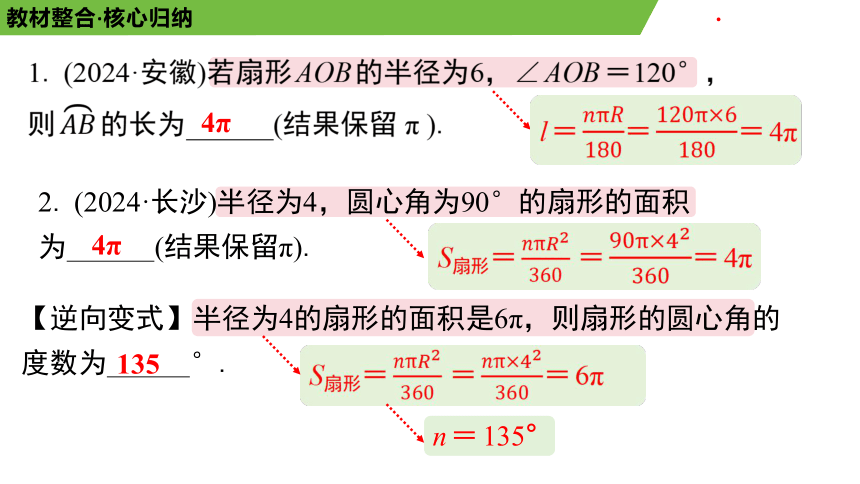
1. (2024·安徽)若扇形AOB的半径为6,∠AOB=120°,
则 的长为 (结果保留 π ).
【逆向变式】半径为4的扇形的面积是6π,则扇形的圆心角的度数为 °.
4π
4π
135
l===4π
S扇形= ==4π
2. (2024·长沙)半径为4,圆心角为90°的扇形的面积为 (结果保留π).
S扇形= ==6π
n=135°
名称 圆周长 扇形弧长 圆面积 扇形面积
公式 C= l= S= S扇形= = Rl 2πR
πR2
概念 (1)圆锥的母线长l等于其侧面展开图扇形的半径; (2)圆锥的轴截面是等腰三角形,圆锥的母线l和底面圆半径r、圆锥的高h,这三个量之间的数量关系为r2+h2= ; (3)圆锥底面圆的周长等于其侧面展开图扇形的弧长, 即2πr= ,所以扇形的圆心角α=
计算 公式 (1)底面周长:C=2πr(底面为圆); (2)底面面积:S底=πr2(底面为圆); (3)侧面积:S侧= l·2πr=πrl(侧面展开图为扇形); (4)全面积=S底+S侧=πr2 +πrl l2
考点 弧长及扇形面积【长沙T14】
考点 圆锥
边心距 r=
周长 正多边形的周长L=na 面积 正多边形的面积S= Lr= nar 中心角 θ=
考点 圆与正多边形
重难精讲
变式探究
03
第六单元 第28讲
例 如图①,正方形ABCD是半径为R的☉O的内接四边形,
R=6.
(1)求弧AD的长;2π·6=3π,∴弧AD的长为3π.
解:如图①,连接OA,OD,
则∠AOD=90°.
弧AD的长= ·2πR= ·2π·6=3π,
∴弧AD的长为3π.
l=
求证弧AD所对的圆心角
连接OA,OD
∠AOD=90°
l=
(2)求正方形ABCD的边长和边心距;方形ABCD的边长
为6 ,边心距为3 .
解:如图①,过点O作OE⊥BC,垂足为点E.
∵正方形ABCD为☉O的内接四边形,
∴∠BOC= =90°,∠OBC=45°,OB=6.
∴BE=OE,在Rt△OBE中,∠BEO=90°,
由勾股定理可得OE=BE= OB=3 .
∴BC=2BE=6 .即半径为6的圆内接
正方形ABCD的边长为6 ,边心距为3 .
例 如图①,正方形ABCD是半径为R的☉O的内接四边形,R=6.OD,
6
E
过点O作OE⊥BC
∠OBC=45°
由勾股定理可得
OE=BE= OB=3
BC=2BE=6
(3)过圆心O的直线MN交圆于点M,N,如下图②所示,求图中阴影部分的面积.
解:如图②,连接OD,
由全等得S阴影=S扇形DOC-S△DOC.
∵S扇形DOC= ×π×62=9π,
S△DOC= ×6 ×3 =18,
∴S阴影=9π-18.
S扇形=
连接OD
S阴影=S扇形DOC-S△DOC
正方形ABCD的边长为6 ,边心距为3
例 如图①,正方形ABCD是半径为R的☉O的内接四边形,R=6.OD,
1. 传统服饰日益受到关注,如下图①为明清时期女子主要裙式
之一的马面裙,如下图②马面裙可以近似地看作扇形的一部
分,其中 的长度为 米,裙长AB=0.8米,
圆心角∠AOD=60°,则OB的长为 米.
1.8
第1题图
【变式设问】马面裙的面积为 平方米(结果保留π).
π
R=1
l===
OB=AB+OA=1.8
S阴影=S扇形OBC-S扇形OAD=
2. (2024·通辽)如图,为便于研究圆锥与扇形的关系,
小方同学利用扇形纸片恰好围成一个底面半径为5cm,
母线长为12cm的圆锥的侧面,那么这个
扇形纸片的面积是 cm2
(结果用含π的式子表示).
第2题图
60π
3. (2024·齐齐哈尔)若圆锥的底面半径是1cm,
它的侧面展开图的圆心角是直角,
则该圆锥的高为 cm.
1
S扇形 == Rl
底面圆周长
=弧长=2π
=R×2π
R=4
4
SO=
4. 如右图,正八边形ABCDEFGH的边长为4,
以顶点A为圆心,AB的长为半径画圆,则阴影部分的面积为 (结果保留π).
第4题图
6π
5. (2024·雅安)如图,☉O的周长为8π,
正六边形ABCDEF内接于☉O,则△OAB的面积为( B )
A. 4 B. 4
C. 6 D. 6
第5题图
B
6. (教材素材题)如图,四边形ABCD是正方形,曲线
DA1B1C1D1A2B2…叫作“正方形的渐开线”,其中DA1的圆心
为点A,半径为AD;A1B1的圆心为点B,半径为BA1;B1C1的
圆心为点C,半径为CB1;C1D1的圆心为点D,半径为
DC1;…,DA1,A1B1,B1C1,C1D1,…的圆心依次按A,
B,C,D循环,当AB=1时,则A2024B2024的长
是 .
4047π
第6题图
课堂小结
与圆有关的计算
扇形的弧长
圆柱与圆锥的相关计算
扇形的面积及与圆有关的阴影部分面积的计算
圆与正多边形的相关计算
第28讲 与圆有关的计算
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第六单元 第28讲
课标要求 作业目标
与圆有关的计算 掌握与圆相关的计算如弧长、扇形的面积、圆锥侧面积和全面积. 掌握弧长和扇形面积的公式,并会用其计算弧长和扇形面积,会利用弧长、扇形面积计算公式计算简单组合图形的周长和面积
知道圆锥的侧面展开图是扇形,了解圆锥各部分名称.会计算圆锥的侧面积和全面积
要求与目标
教材整合 核心归纳
02
第六单元 第28讲
1. (2024·安徽)若扇形AOB的半径为6,∠AOB=120°,
则 的长为 (结果保留 π ).
【逆向变式】半径为4的扇形的面积是6π,则扇形的圆心角的度数为 °.
4π
4π
135
l===4π
S扇形= ==4π
2. (2024·长沙)半径为4,圆心角为90°的扇形的面积为 (结果保留π).
S扇形= ==6π
n=135°
名称 圆周长 扇形弧长 圆面积 扇形面积
公式 C= l= S= S扇形= = Rl 2πR
πR2
概念 (1)圆锥的母线长l等于其侧面展开图扇形的半径; (2)圆锥的轴截面是等腰三角形,圆锥的母线l和底面圆半径r、圆锥的高h,这三个量之间的数量关系为r2+h2= ; (3)圆锥底面圆的周长等于其侧面展开图扇形的弧长, 即2πr= ,所以扇形的圆心角α=
计算 公式 (1)底面周长:C=2πr(底面为圆); (2)底面面积:S底=πr2(底面为圆); (3)侧面积:S侧= l·2πr=πrl(侧面展开图为扇形); (4)全面积=S底+S侧=πr2 +πrl l2
考点 弧长及扇形面积【长沙T14】
考点 圆锥
边心距 r=
周长 正多边形的周长L=na 面积 正多边形的面积S= Lr= nar 中心角 θ=
考点 圆与正多边形
重难精讲
变式探究
03
第六单元 第28讲
例 如图①,正方形ABCD是半径为R的☉O的内接四边形,
R=6.
(1)求弧AD的长;2π·6=3π,∴弧AD的长为3π.
解:如图①,连接OA,OD,
则∠AOD=90°.
弧AD的长= ·2πR= ·2π·6=3π,
∴弧AD的长为3π.
l=
求证弧AD所对的圆心角
连接OA,OD
∠AOD=90°
l=
(2)求正方形ABCD的边长和边心距;方形ABCD的边长
为6 ,边心距为3 .
解:如图①,过点O作OE⊥BC,垂足为点E.
∵正方形ABCD为☉O的内接四边形,
∴∠BOC= =90°,∠OBC=45°,OB=6.
∴BE=OE,在Rt△OBE中,∠BEO=90°,
由勾股定理可得OE=BE= OB=3 .
∴BC=2BE=6 .即半径为6的圆内接
正方形ABCD的边长为6 ,边心距为3 .
例 如图①,正方形ABCD是半径为R的☉O的内接四边形,R=6.OD,
6
E
过点O作OE⊥BC
∠OBC=45°
由勾股定理可得
OE=BE= OB=3
BC=2BE=6
(3)过圆心O的直线MN交圆于点M,N,如下图②所示,求图中阴影部分的面积.
解:如图②,连接OD,
由全等得S阴影=S扇形DOC-S△DOC.
∵S扇形DOC= ×π×62=9π,
S△DOC= ×6 ×3 =18,
∴S阴影=9π-18.
S扇形=
连接OD
S阴影=S扇形DOC-S△DOC
正方形ABCD的边长为6 ,边心距为3
例 如图①,正方形ABCD是半径为R的☉O的内接四边形,R=6.OD,
1. 传统服饰日益受到关注,如下图①为明清时期女子主要裙式
之一的马面裙,如下图②马面裙可以近似地看作扇形的一部
分,其中 的长度为 米,裙长AB=0.8米,
圆心角∠AOD=60°,则OB的长为 米.
1.8
第1题图
【变式设问】马面裙的面积为 平方米(结果保留π).
π
R=1
l===
OB=AB+OA=1.8
S阴影=S扇形OBC-S扇形OAD=
2. (2024·通辽)如图,为便于研究圆锥与扇形的关系,
小方同学利用扇形纸片恰好围成一个底面半径为5cm,
母线长为12cm的圆锥的侧面,那么这个
扇形纸片的面积是 cm2
(结果用含π的式子表示).
第2题图
60π
3. (2024·齐齐哈尔)若圆锥的底面半径是1cm,
它的侧面展开图的圆心角是直角,
则该圆锥的高为 cm.
1
S扇形 == Rl
底面圆周长
=弧长=2π
=R×2π
R=4
4
SO=
4. 如右图,正八边形ABCDEFGH的边长为4,
以顶点A为圆心,AB的长为半径画圆,则阴影部分的面积为 (结果保留π).
第4题图
6π
5. (2024·雅安)如图,☉O的周长为8π,
正六边形ABCDEF内接于☉O,则△OAB的面积为( B )
A. 4 B. 4
C. 6 D. 6
第5题图
B
6. (教材素材题)如图,四边形ABCD是正方形,曲线
DA1B1C1D1A2B2…叫作“正方形的渐开线”,其中DA1的圆心
为点A,半径为AD;A1B1的圆心为点B,半径为BA1;B1C1的
圆心为点C,半径为CB1;C1D1的圆心为点D,半径为
DC1;…,DA1,A1B1,B1C1,C1D1,…的圆心依次按A,
B,C,D循环,当AB=1时,则A2024B2024的长
是 .
4047π
第6题图
课堂小结
与圆有关的计算
扇形的弧长
圆柱与圆锥的相关计算
扇形的面积及与圆有关的阴影部分面积的计算
圆与正多边形的相关计算
同课章节目录
