第30讲 图形的平移、旋转与对称 2025年中考一轮数学专题复习课件(湖南)(共27张PPT)
文档属性
| 名称 | 第30讲 图形的平移、旋转与对称 2025年中考一轮数学专题复习课件(湖南)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-03 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第30讲
图形的平移、旋转与对称
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第七单元 第30讲
课标要求 作业目标
图形旋转 1.通过具体实例认识平面图形关于旋转中心的旋转. 2.探索它的基本性质:一个图形和旋转得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等. 3.了解中心对称、中心对称图形的概念,探索它们的基本性质:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分. 4.探索线段、平行四边形、正多边形、圆的中心对称性质. 5.认识并欣赏自然界和现实生活中的中心对称图形。 认识生产生活中的旋转现象,了解平面图形旋转的概念,掌握图形旋转的性质,会根据旋转性质画出简单平面图形旋转后的图形
会运用旋转变换选择不同的旋转中心、不同的旋转角进行简单的图形设计
了解中心对称的概念,知道中心对称和轴对称的区别和联系,掌握中心对称的性质,会画出和已知图形关于已知点对称的图形,会找出两个图形关于某点对称时的对称中心
了解中心对称图形的概念,知道中心对称和中心对称图形的区别和联系,认识并欣赏自然界和现实中常见的中心对称图形,能辨析几何图形中常见的中心对称图形
掌握直角坐标系中关于原点对称的点的坐标的特征,会画出和已知图形关于原点对称的图形
要求与目标
课标要求 作业目标
图形平移 1.通过具体实例认识平移,探索它的基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等。 2.认识并欣赏平移在自然界和现实生活中的应用。 3.运用图形的轴对称、旋转、平移进行图案设计. 掌握基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等
在平面直角坐标系中,能用坐标表示平移,通过研究平移与坐标的关系,体会数形结合的思想
要求与目标
教材整合 核心归纳
02
第七单元 第30讲
1. 把边长为3cm的正方形ABCD先向右平移1cm,
再向上平移1cm,得到正方形EFGH,
则重叠部分的面积为 cm2.
2. 如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点
B的对应点D落在边AC的延长线上,若AB=12,AE=7,则
线段CD的长为 .
4
5
2
△ABC≌△ADE
AB=AD=12,AC=AE=7
CD=AD-AC=12-7=5
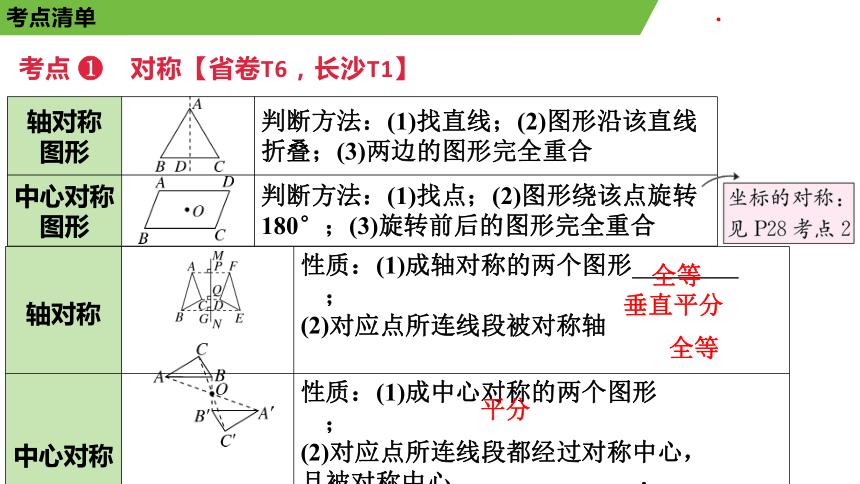
轴对称 图形 判断方法:(1)找直线;(2)图形沿该直线折叠;(3)两边的图形完全重合
中心对称 图形 判断方法:(1)找点;(2)图形绕该点旋转180°;(3)旋转前后的图形完全重合
考点 对称【省卷T6,长沙T1】
轴对称 性质:(1)成轴对称的两个图形 ;
(2)对应点所连线段被对称轴
中心对称 性质:(1)成中心对称的两个图形 ;
(2)对应点所连线段都经过对称中心,
且被对称中心 ;
(3)对应线段互相平行(或在一条直线上)
全等
垂直平分
全等
平分
考点清单
要素 (1)平移方向;(2)平移距离
性质 (1)全等,对应线段平行(或在一条直线上)且相等,对应角相等.如左图,△ABC≌ ,AB= ,
BC= ,AB∥ ,AC∥ ,
∠A= ,∠B= ;
(2)对应点所连线段平行(或在一条直线上)且相等.如左图, AA'∥BB'∥ ,AA'= =CC'
△A'B'C'
A'B'
B'C'
A'B'
A'C'
∠A'
∠B'
CC'
BB'
考点 平移
要素 (1)旋转中心(点O);(2)旋转方向(顺时针);(3)旋转角
性质
(1)对应点到旋转中心的距离相等.如左图,
AO= ,BO= ,CO= ;
(2)对应点与旋转中心所连线段的夹角等于旋转角.如左图,∠AOA'= = =旋转角;
(3)旋转前后的图形全等.如左图,△ABC≌
A'O
B'O
C'O
∠BOB'
∠COC'
△A'B'C'
考点 旋转
考点清单
重难精讲
变式探究
03
第七单元 第30讲
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得△DEC,
点D恰好在AB上.
(1)若AC=4,求DE的长;解:(1)∵在Rt△ABC中,∠ACB=90°,∠ABC=30°,
AC=4,∴AB=2AC=8.∵将△ABC绕点C顺时针旋转一定
角度得到△DEC,∴DE=AB=8.
解:∵在Rt△ABC中,∠ACB=90°,
∠ABC=30°,AC=4,
∴AB=2AC=8.
∵将△ABC绕点C顺时针旋转一定
角度得到△DEC,∴DE=AB=8.
例题图
AB=8
DE=AB=8
(2)确定△ACD的形状,并说明理由;
解:(2)△ACD是等边三角形.理由如下:
∵∠ACB=90°,∠ABC=30°,∴∠A=60°.
∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴AC=CD. ∴△ACD是等边三角形.
解:△ACD是等边三角形.理由如下:
∵∠ACB=90°,∠ABC=30°,
∴∠A=60°.
∵将△ABC绕点C顺时针旋转
一定角度得到△DEC,
∴AC=CD. ∴△ACD是等边三角形.
例题图
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得△DEC,
点D恰好在AB上.解:(1)∵在Rt△ABC中,∠ACB=90°,
∠A=60°
AC=CD
△ACD是等边三角形
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得△DEC,
点D恰好在AB上.
(3)连接BE,确定△BCE的形状,并说明理由;
解:(3)△BCE为等边三角形.理由如下:∵△ABC绕点C顺时
针旋转一定角度得到△DEC,
∴BC=EC,∠ACB
解:△BCE为等边三角形.理由如下:
∵△ABC绕点C顺时针旋转一定角度得到△DEC,
∴BC=EC,∠ACB=∠DCE.
∴∠ACB-∠DCB=∠DCE-∠DCB.
∴∠ACD=∠BCE.
由(2)得△ACD是等边三角形,∴∠BCE=∠ACD=60°.
∴△BCE是等边三角形.
例题图
BC=EC,∠ACB=∠DCE
∠DCB是共角
∠ACD=∠BCE=60°
△BCE是
等边三角形
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(4) 若CE=8,点K为直线DE上的一点,
求AK+CK的最小值.
例题图
作 B点或 C 点关于直线DE的对称点
∠DEC=∠ABC=30°,BC=CE=8
30°
30°
由(3)知△BCE是等边三角形
8
8
∠BED=∠DEC=30°
30°
△DBE≌△DCE
点B与点C关于直线DE对称
当K与D重合时,AK+CK最小
最小值=AB= = =
解:∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴∠DEC=∠ABC=30°,BC=CE=8.
由(3)知△BCE是等边三角形,
∴∠BED=∠DEC=30°.
在△DBE和△DCE中,
∴△DBE≌△DCE(SAS).
∴BD=CD,即点B与点C关于直线DE对称.
∵K为直线DE上的一点,∴BK=CK.
∴当K与D重合时,AK+CK最小,最小值=AB= = = .
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(4) 若CE=8,点K为直线DE上的一点,求AK+CK的最小值.
1. (2024·长沙)下列图形中,既是轴对称图形又是中心对称图形
的是( B )
B
2. (2024·河北)如下图,AD与BC交于点O,△ABO和△CDO
关于直线PQ对称,点A,B的对称点分别是点C,D. 下列不
一定正确的是( A )
A. AD⊥BC B. AC⊥PQ
C. △ABO≌△CDO D. AC∥BD
A
第2题图
3. (2023·株洲)如图,在矩形ABCD中,AB>AD,AC与BD
相交于点O,下列说法正确的是( A )
A. 点O为矩形ABCD的对称中心
B. 点O为线段AB的对称中心
C. 直线BD为矩形ABCD的对称轴
D. 直线AC为线段BD的对称轴
第3题图
A
4. 如下图,在Rt△ABC中,∠C=90°,BC<AC. 点D,E
分别在边AB,BC上,连接DE,将△BDE沿DE折叠,点B的
对应点为点B'.若点B'刚好落在边AC上,∠CB'E=30°,
CE=3,则BC的长为 .
第4题图
9
3
30°
B'E=6
B'E=BE=6
BC=CE+BE=9
6
6
5. (2022·怀化)如图,△ABC沿BC方向平移后得到△DEF,
已知BC=5,EC=2,则平移的距离是( C )
A. 1 B. 2 C. 3 D. 4
第5题图
C
【变式题】如右图,已知∠ACB=90°,
∠A=30°,BC=2cm,把△ABC沿AB方向平移1cm,
得到△A'B'C',连接CC',
则四边形AB'C'C的周长为 cm.
(8+2 )
变式题图
6. (2023·衡阳二模改编)下图是一块矩形ABCD的场地,长AB
=99m,宽AD=41m,从A,B两处入口的路宽都为1m,两小
路汇合处路口宽为2m,其余部分种植草坪,则草坪的面积
为 m2.
第6题图
3880
7. (2023·益阳)如图,在正方形ABCD中,AB=4,点E为AB
的中点,连接DE,将△DAE绕点D按逆时针方向旋转90°得
到△DCF,连接EF,则EF的长为 .
第7题图
2
8. (2023·长沙岳麓区三模)如下图,在Rt△ABC中,∠C=90°,∠BAC=50°,将△ABC绕点A逆时针旋转得到△AB'C',使点C'落在AB边上,连接BB',则∠BB'C' 的度数为 °.
第8题图
25
9. 银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如
上图是一片银杏叶标本,叶片上两点B,C的坐标分别为
(-3,2),(4,3),将银杏叶绕原点顺时针旋转90°后,叶柄上点A对应点的坐标为 .
第9题图
(-3,1)
x
y
O
A′
10. (2022·常德)如下图,在Rt△ABC中,∠ABC=90°,
∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,
点A,B的对应点分别是点D,E,点F是边AC的中点,连接
BF,BE,FD,则下列结论错误的是( D )
A. BE=BC B. BF∥DE,BF=DE
C. ∠DFC=90° D. DG=3GF
第10题图
D
11. (2024·龙东)如下图,在正方形网格中,每个小正方形的边
长都是1个单位长度.在平面直角坐标系中,△ABC的三个顶点
坐标分别为A(-1,1),B(-2,3),C(-5,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点B1的坐标;
第11题图
解:△A1B1C1如图所示,
点B1的坐标为(2,3).
(2)画出△ABC绕点A逆时针旋转90°后得到的△AB2C2,并写出点B2的坐标;
解:△AB2C2如图所示,
点B2的坐标为(-3,0).
(3)在(2)的条件下,求点B旋转到点B2的过程中所经过的路径长
(结果保留π).
11. (2024·龙东)如下图,在正方形网格中,每个小正方形的边
长都是1个单位长度.在平面直角坐标系中,△ABC的三个顶点
坐标分别为A(-1,1),B(-2,3),C(-5,2).
第11题图
解:∵AB= = ,∠BAB2=90°,
∴点B旋转到点B2的过程中所经过的路径
长为 = π.
课堂小结
图形的对称、平移与旋转
轴对称图形与轴对称
性质
图形的对称
图形的平移
中心对称图形与中心对称
定义
两要素
图形的旋转
性质
定义
三要素
第30讲
图形的平移、旋转与对称
目录
CONTENTS
1
2
3
课标要求 作业目标
教材整合·核心归纳
重点精讲·变式探究
课标要求 作业目标
01
第七单元 第30讲
课标要求 作业目标
图形旋转 1.通过具体实例认识平面图形关于旋转中心的旋转. 2.探索它的基本性质:一个图形和旋转得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等. 3.了解中心对称、中心对称图形的概念,探索它们的基本性质:成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分. 4.探索线段、平行四边形、正多边形、圆的中心对称性质. 5.认识并欣赏自然界和现实生活中的中心对称图形。 认识生产生活中的旋转现象,了解平面图形旋转的概念,掌握图形旋转的性质,会根据旋转性质画出简单平面图形旋转后的图形
会运用旋转变换选择不同的旋转中心、不同的旋转角进行简单的图形设计
了解中心对称的概念,知道中心对称和轴对称的区别和联系,掌握中心对称的性质,会画出和已知图形关于已知点对称的图形,会找出两个图形关于某点对称时的对称中心
了解中心对称图形的概念,知道中心对称和中心对称图形的区别和联系,认识并欣赏自然界和现实中常见的中心对称图形,能辨析几何图形中常见的中心对称图形
掌握直角坐标系中关于原点对称的点的坐标的特征,会画出和已知图形关于原点对称的图形
要求与目标
课标要求 作业目标
图形平移 1.通过具体实例认识平移,探索它的基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等。 2.认识并欣赏平移在自然界和现实生活中的应用。 3.运用图形的轴对称、旋转、平移进行图案设计. 掌握基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等
在平面直角坐标系中,能用坐标表示平移,通过研究平移与坐标的关系,体会数形结合的思想
要求与目标
教材整合 核心归纳
02
第七单元 第30讲
1. 把边长为3cm的正方形ABCD先向右平移1cm,
再向上平移1cm,得到正方形EFGH,
则重叠部分的面积为 cm2.
2. 如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点
B的对应点D落在边AC的延长线上,若AB=12,AE=7,则
线段CD的长为 .
4
5
2
△ABC≌△ADE
AB=AD=12,AC=AE=7
CD=AD-AC=12-7=5
轴对称 图形 判断方法:(1)找直线;(2)图形沿该直线折叠;(3)两边的图形完全重合
中心对称 图形 判断方法:(1)找点;(2)图形绕该点旋转180°;(3)旋转前后的图形完全重合
考点 对称【省卷T6,长沙T1】
轴对称 性质:(1)成轴对称的两个图形 ;
(2)对应点所连线段被对称轴
中心对称 性质:(1)成中心对称的两个图形 ;
(2)对应点所连线段都经过对称中心,
且被对称中心 ;
(3)对应线段互相平行(或在一条直线上)
全等
垂直平分
全等
平分
考点清单
要素 (1)平移方向;(2)平移距离
性质 (1)全等,对应线段平行(或在一条直线上)且相等,对应角相等.如左图,△ABC≌ ,AB= ,
BC= ,AB∥ ,AC∥ ,
∠A= ,∠B= ;
(2)对应点所连线段平行(或在一条直线上)且相等.如左图, AA'∥BB'∥ ,AA'= =CC'
△A'B'C'
A'B'
B'C'
A'B'
A'C'
∠A'
∠B'
CC'
BB'
考点 平移
要素 (1)旋转中心(点O);(2)旋转方向(顺时针);(3)旋转角
性质
(1)对应点到旋转中心的距离相等.如左图,
AO= ,BO= ,CO= ;
(2)对应点与旋转中心所连线段的夹角等于旋转角.如左图,∠AOA'= = =旋转角;
(3)旋转前后的图形全等.如左图,△ABC≌
A'O
B'O
C'O
∠BOB'
∠COC'
△A'B'C'
考点 旋转
考点清单
重难精讲
变式探究
03
第七单元 第30讲
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得△DEC,
点D恰好在AB上.
(1)若AC=4,求DE的长;解:(1)∵在Rt△ABC中,∠ACB=90°,∠ABC=30°,
AC=4,∴AB=2AC=8.∵将△ABC绕点C顺时针旋转一定
角度得到△DEC,∴DE=AB=8.
解:∵在Rt△ABC中,∠ACB=90°,
∠ABC=30°,AC=4,
∴AB=2AC=8.
∵将△ABC绕点C顺时针旋转一定
角度得到△DEC,∴DE=AB=8.
例题图
AB=8
DE=AB=8
(2)确定△ACD的形状,并说明理由;
解:(2)△ACD是等边三角形.理由如下:
∵∠ACB=90°,∠ABC=30°,∴∠A=60°.
∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴AC=CD. ∴△ACD是等边三角形.
解:△ACD是等边三角形.理由如下:
∵∠ACB=90°,∠ABC=30°,
∴∠A=60°.
∵将△ABC绕点C顺时针旋转
一定角度得到△DEC,
∴AC=CD. ∴△ACD是等边三角形.
例题图
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得△DEC,
点D恰好在AB上.解:(1)∵在Rt△ABC中,∠ACB=90°,
∠A=60°
AC=CD
△ACD是等边三角形
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得△DEC,
点D恰好在AB上.
(3)连接BE,确定△BCE的形状,并说明理由;
解:(3)△BCE为等边三角形.理由如下:∵△ABC绕点C顺时
针旋转一定角度得到△DEC,
∴BC=EC,∠ACB
解:△BCE为等边三角形.理由如下:
∵△ABC绕点C顺时针旋转一定角度得到△DEC,
∴BC=EC,∠ACB=∠DCE.
∴∠ACB-∠DCB=∠DCE-∠DCB.
∴∠ACD=∠BCE.
由(2)得△ACD是等边三角形,∴∠BCE=∠ACD=60°.
∴△BCE是等边三角形.
例题图
BC=EC,∠ACB=∠DCE
∠DCB是共角
∠ACD=∠BCE=60°
△BCE是
等边三角形
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,
∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(4) 若CE=8,点K为直线DE上的一点,
求AK+CK的最小值.
例题图
作 B点或 C 点关于直线DE的对称点
∠DEC=∠ABC=30°,BC=CE=8
30°
30°
由(3)知△BCE是等边三角形
8
8
∠BED=∠DEC=30°
30°
△DBE≌△DCE
点B与点C关于直线DE对称
当K与D重合时,AK+CK最小
最小值=AB= = =
解:∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴∠DEC=∠ABC=30°,BC=CE=8.
由(3)知△BCE是等边三角形,
∴∠BED=∠DEC=30°.
在△DBE和△DCE中,
∴△DBE≌△DCE(SAS).
∴BD=CD,即点B与点C关于直线DE对称.
∵K为直线DE上的一点,∴BK=CK.
∴当K与D重合时,AK+CK最小,最小值=AB= = = .
例 改编问题链 如下图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(4) 若CE=8,点K为直线DE上的一点,求AK+CK的最小值.
1. (2024·长沙)下列图形中,既是轴对称图形又是中心对称图形
的是( B )
B
2. (2024·河北)如下图,AD与BC交于点O,△ABO和△CDO
关于直线PQ对称,点A,B的对称点分别是点C,D. 下列不
一定正确的是( A )
A. AD⊥BC B. AC⊥PQ
C. △ABO≌△CDO D. AC∥BD
A
第2题图
3. (2023·株洲)如图,在矩形ABCD中,AB>AD,AC与BD
相交于点O,下列说法正确的是( A )
A. 点O为矩形ABCD的对称中心
B. 点O为线段AB的对称中心
C. 直线BD为矩形ABCD的对称轴
D. 直线AC为线段BD的对称轴
第3题图
A
4. 如下图,在Rt△ABC中,∠C=90°,BC<AC. 点D,E
分别在边AB,BC上,连接DE,将△BDE沿DE折叠,点B的
对应点为点B'.若点B'刚好落在边AC上,∠CB'E=30°,
CE=3,则BC的长为 .
第4题图
9
3
30°
B'E=6
B'E=BE=6
BC=CE+BE=9
6
6
5. (2022·怀化)如图,△ABC沿BC方向平移后得到△DEF,
已知BC=5,EC=2,则平移的距离是( C )
A. 1 B. 2 C. 3 D. 4
第5题图
C
【变式题】如右图,已知∠ACB=90°,
∠A=30°,BC=2cm,把△ABC沿AB方向平移1cm,
得到△A'B'C',连接CC',
则四边形AB'C'C的周长为 cm.
(8+2 )
变式题图
6. (2023·衡阳二模改编)下图是一块矩形ABCD的场地,长AB
=99m,宽AD=41m,从A,B两处入口的路宽都为1m,两小
路汇合处路口宽为2m,其余部分种植草坪,则草坪的面积
为 m2.
第6题图
3880
7. (2023·益阳)如图,在正方形ABCD中,AB=4,点E为AB
的中点,连接DE,将△DAE绕点D按逆时针方向旋转90°得
到△DCF,连接EF,则EF的长为 .
第7题图
2
8. (2023·长沙岳麓区三模)如下图,在Rt△ABC中,∠C=90°,∠BAC=50°,将△ABC绕点A逆时针旋转得到△AB'C',使点C'落在AB边上,连接BB',则∠BB'C' 的度数为 °.
第8题图
25
9. 银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如
上图是一片银杏叶标本,叶片上两点B,C的坐标分别为
(-3,2),(4,3),将银杏叶绕原点顺时针旋转90°后,叶柄上点A对应点的坐标为 .
第9题图
(-3,1)
x
y
O
A′
10. (2022·常德)如下图,在Rt△ABC中,∠ABC=90°,
∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,
点A,B的对应点分别是点D,E,点F是边AC的中点,连接
BF,BE,FD,则下列结论错误的是( D )
A. BE=BC B. BF∥DE,BF=DE
C. ∠DFC=90° D. DG=3GF
第10题图
D
11. (2024·龙东)如下图,在正方形网格中,每个小正方形的边
长都是1个单位长度.在平面直角坐标系中,△ABC的三个顶点
坐标分别为A(-1,1),B(-2,3),C(-5,2).
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点B1的坐标;
第11题图
解:△A1B1C1如图所示,
点B1的坐标为(2,3).
(2)画出△ABC绕点A逆时针旋转90°后得到的△AB2C2,并写出点B2的坐标;
解:△AB2C2如图所示,
点B2的坐标为(-3,0).
(3)在(2)的条件下,求点B旋转到点B2的过程中所经过的路径长
(结果保留π).
11. (2024·龙东)如下图,在正方形网格中,每个小正方形的边
长都是1个单位长度.在平面直角坐标系中,△ABC的三个顶点
坐标分别为A(-1,1),B(-2,3),C(-5,2).
第11题图
解:∵AB= = ,∠BAB2=90°,
∴点B旋转到点B2的过程中所经过的路径
长为 = π.
课堂小结
图形的对称、平移与旋转
轴对称图形与轴对称
性质
图形的对称
图形的平移
中心对称图形与中心对称
定义
两要素
图形的旋转
性质
定义
三要素
同课章节目录
