9.1.1认识三角形课时作业(含解析)
文档属性
| 名称 | 9.1.1认识三角形课时作业(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 93.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 23:02:53 | ||
图片预览

文档简介
9.1.1认识三角形课时作业
一、选择题(每小题4分,共12分)
1.下列说法中,不正确的是 ( )
A.△ABC中,BC边上的高是过顶点A向对边所在的直线引的垂线
B.△ABC中,BC边上的高是过顶点A向对边所在的直线引的垂线段
C.三角形的角平分线不是射线
D.三角形的高可能在三角形的外部
2.如图所示,在△ABC中,∠ACB是钝角,让点C在射线BD上向右移动,则 ( )
A.△ABC将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形
B.△ABC将变成锐角三角形,而不会再是钝角三角形
C.△ABC将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形
D.△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形
3.图中三角形的个数是 ( )
A.8 B.9 C.10 D.11
二、填空题(每小题4分,共12分)
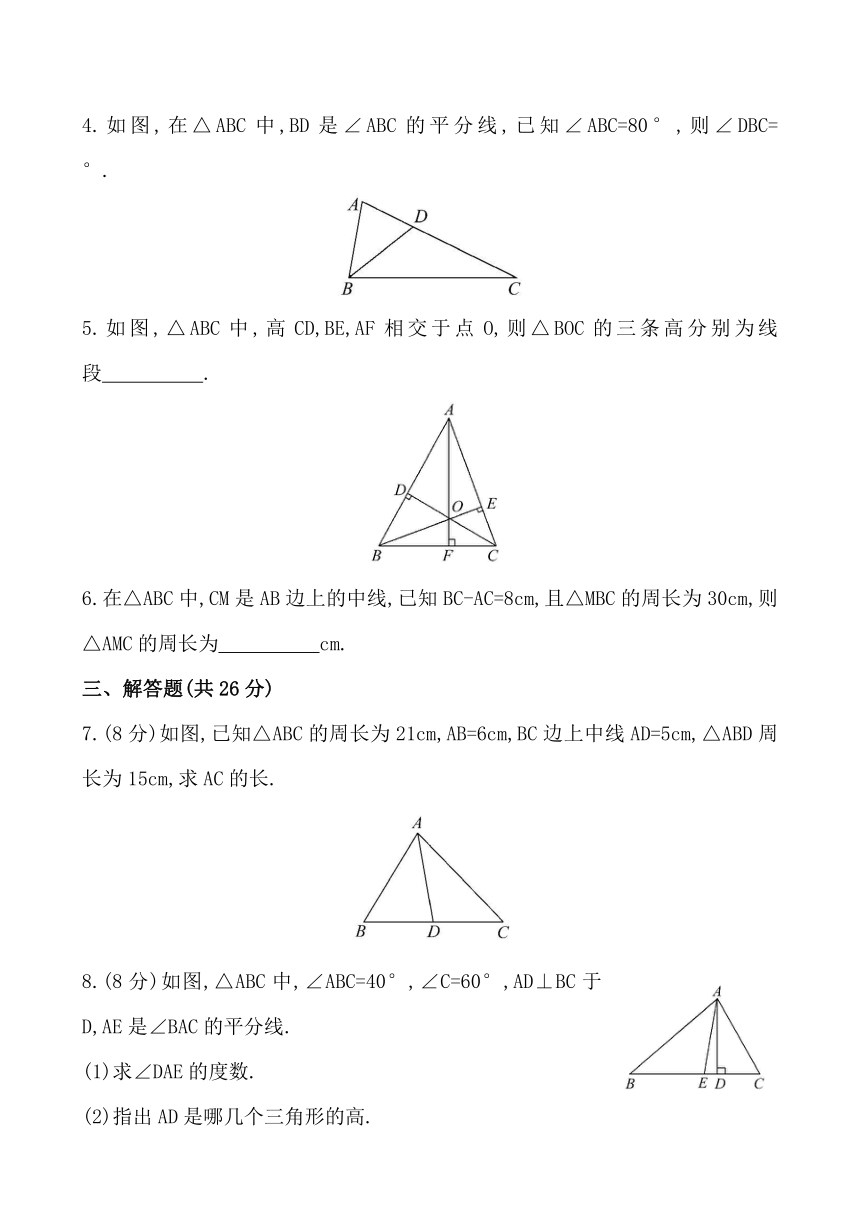
4.如图,在△ABC中,BD是∠ABC的平分线,已知∠ABC=80°,则∠DBC= °.
5.如图,△ABC中,高CD,BE,AF相交于点O,则△BOC的三条高分别为线段 .
6.在△ABC中,CM是AB边上的中线,已知BC-AC=8cm,且△MBC的周长为30cm,则△AMC的周长为 cm.
三、解答题(共26分)
7.(8分)如图,已知△ABC的周长为21cm,AB=6cm,BC边上中线AD=5cm,△ABD周长为15cm,求AC的长.
8.(8分)如图,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数.
(2)指出AD是哪几个三角形的高.
【拓展延伸】
9.(10分)如图,在网格中有一个直角三角形(网格中的每个小正方形的边长均为1个单位长度),若以该三角形一边为公共边画一个新三角形与原来的直角三角形一起组成一个等腰三角形.要求新三角形与原来的直角三角形除了有一条公共边外,没有其他的公共点,新三角形的顶点不一定在格点上.那么符合要求的新三角形有多少个?
答案解析
1.【解析】选A.三角形的高是条垂线段,A错误;B正确;三角形的角平分线不是射线,而是线段,C正确;D叙述的是钝角三角形的高.
2.【解析】选D.根据变化规律可知:△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形.
3.【解析】选B.图中的三角形分别为:△BDE,△DEF,△EFG,△FGA,△AGC,△BEF,△BFG,△ABG,△ABC,共9个.
4.【解析】∵BD是∠ABC的平分线,∠ABC=80°,
∴∠DBC=∠ABD=∠ABC=×80°=40°.
答案:40
5.【解析】△BOC的三条边分别为BC,BO,OC,所以BC边上的高为OF;BO边上的高为CE;CO边上的高为BD.
答案:OF,CE,BD
6.【解析】因为CM是AB边上的中线,BC-AC=8cm,
所以△MBC的周长比△AMC的周长大8cm,
所以△AMC的周长为22cm.
答案:22
7.【解析】∵AB=6cm,AD=5cm,△ABD周长为15cm,
∴BD=15-6-5=4(cm).
∵AD是BC边上的中线,
∴BC=8cm.
∵△ABC的周长为21cm,
∴AC=21-6-8=7(cm).
故AC的长为7cm.
8.【解析】(1)∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∵∠ABC=40°,∠C=60°,
∴∠BAD=50°,∠CAD=30°,
∴∠BAC=50°+30°=80°,
∵AE是∠BAC的平分线,
∴∠BAE=40°,
∴∠DAE=50°-40°=10°.
(2)AD是△ABE,△ABD,△ABC,△AED,△AEC,△ADC的高.
9.【解析】如图所示,符合条件的新三角形共有7个,在△P1BC中,BP1=BC;
在△P2BC中,BP2=BC;在△P3AC中,P3A=CA;在△P4AC中,AC=P4C;在△P5AC中,P5A=P5C;在△P6AC中,P6A=CA;在△P7CA中,AC=P7C.
一、选择题(每小题4分,共12分)
1.下列说法中,不正确的是 ( )
A.△ABC中,BC边上的高是过顶点A向对边所在的直线引的垂线
B.△ABC中,BC边上的高是过顶点A向对边所在的直线引的垂线段
C.三角形的角平分线不是射线
D.三角形的高可能在三角形的外部
2.如图所示,在△ABC中,∠ACB是钝角,让点C在射线BD上向右移动,则 ( )
A.△ABC将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形
B.△ABC将变成锐角三角形,而不会再是钝角三角形
C.△ABC将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形
D.△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形
3.图中三角形的个数是 ( )
A.8 B.9 C.10 D.11
二、填空题(每小题4分,共12分)
4.如图,在△ABC中,BD是∠ABC的平分线,已知∠ABC=80°,则∠DBC= °.
5.如图,△ABC中,高CD,BE,AF相交于点O,则△BOC的三条高分别为线段 .
6.在△ABC中,CM是AB边上的中线,已知BC-AC=8cm,且△MBC的周长为30cm,则△AMC的周长为 cm.
三、解答题(共26分)
7.(8分)如图,已知△ABC的周长为21cm,AB=6cm,BC边上中线AD=5cm,△ABD周长为15cm,求AC的长.
8.(8分)如图,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数.
(2)指出AD是哪几个三角形的高.
【拓展延伸】
9.(10分)如图,在网格中有一个直角三角形(网格中的每个小正方形的边长均为1个单位长度),若以该三角形一边为公共边画一个新三角形与原来的直角三角形一起组成一个等腰三角形.要求新三角形与原来的直角三角形除了有一条公共边外,没有其他的公共点,新三角形的顶点不一定在格点上.那么符合要求的新三角形有多少个?
答案解析
1.【解析】选A.三角形的高是条垂线段,A错误;B正确;三角形的角平分线不是射线,而是线段,C正确;D叙述的是钝角三角形的高.
2.【解析】选D.根据变化规律可知:△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形.
3.【解析】选B.图中的三角形分别为:△BDE,△DEF,△EFG,△FGA,△AGC,△BEF,△BFG,△ABG,△ABC,共9个.
4.【解析】∵BD是∠ABC的平分线,∠ABC=80°,
∴∠DBC=∠ABD=∠ABC=×80°=40°.
答案:40
5.【解析】△BOC的三条边分别为BC,BO,OC,所以BC边上的高为OF;BO边上的高为CE;CO边上的高为BD.
答案:OF,CE,BD
6.【解析】因为CM是AB边上的中线,BC-AC=8cm,
所以△MBC的周长比△AMC的周长大8cm,
所以△AMC的周长为22cm.
答案:22
7.【解析】∵AB=6cm,AD=5cm,△ABD周长为15cm,
∴BD=15-6-5=4(cm).
∵AD是BC边上的中线,
∴BC=8cm.
∵△ABC的周长为21cm,
∴AC=21-6-8=7(cm).
故AC的长为7cm.
8.【解析】(1)∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∵∠ABC=40°,∠C=60°,
∴∠BAD=50°,∠CAD=30°,
∴∠BAC=50°+30°=80°,
∵AE是∠BAC的平分线,
∴∠BAE=40°,
∴∠DAE=50°-40°=10°.
(2)AD是△ABE,△ABD,△ABC,△AED,△AEC,△ADC的高.
9.【解析】如图所示,符合条件的新三角形共有7个,在△P1BC中,BP1=BC;
在△P2BC中,BP2=BC;在△P3AC中,P3A=CA;在△P4AC中,AC=P4C;在△P5AC中,P5A=P5C;在△P6AC中,P6A=CA;在△P7CA中,AC=P7C.
