9.1.2三角形的内角和与外角和课时作业(含解析)
文档属性
| 名称 | 9.1.2三角形的内角和与外角和课时作业(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 115.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 23:00:50 | ||
图片预览

文档简介
9.1.2三角形的内角和与外角和课时作业
一、选择题(每小题4分,共12分)
1.三角形的三个外角之比为2∶3∶4,则该三角形的三个外角分别为 ( )
A.80°,120°,160° B.40°,60°,80°
C.100°,60°,20° D.140°,120°,100°
2.直尺与三角尺按如图所示的方式叠放在一起,在图中所标记的角中,与∠1互余的角有几个 ( )
A.2个 B.3个 C.4个 D.5个
3.如图,∠1=100°,∠C=70°,则∠A的大小是 ( )
A.10° B.20° C.30° D.80°
二、填空题(每小题4分,共12分)
4.如图是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角是 度.
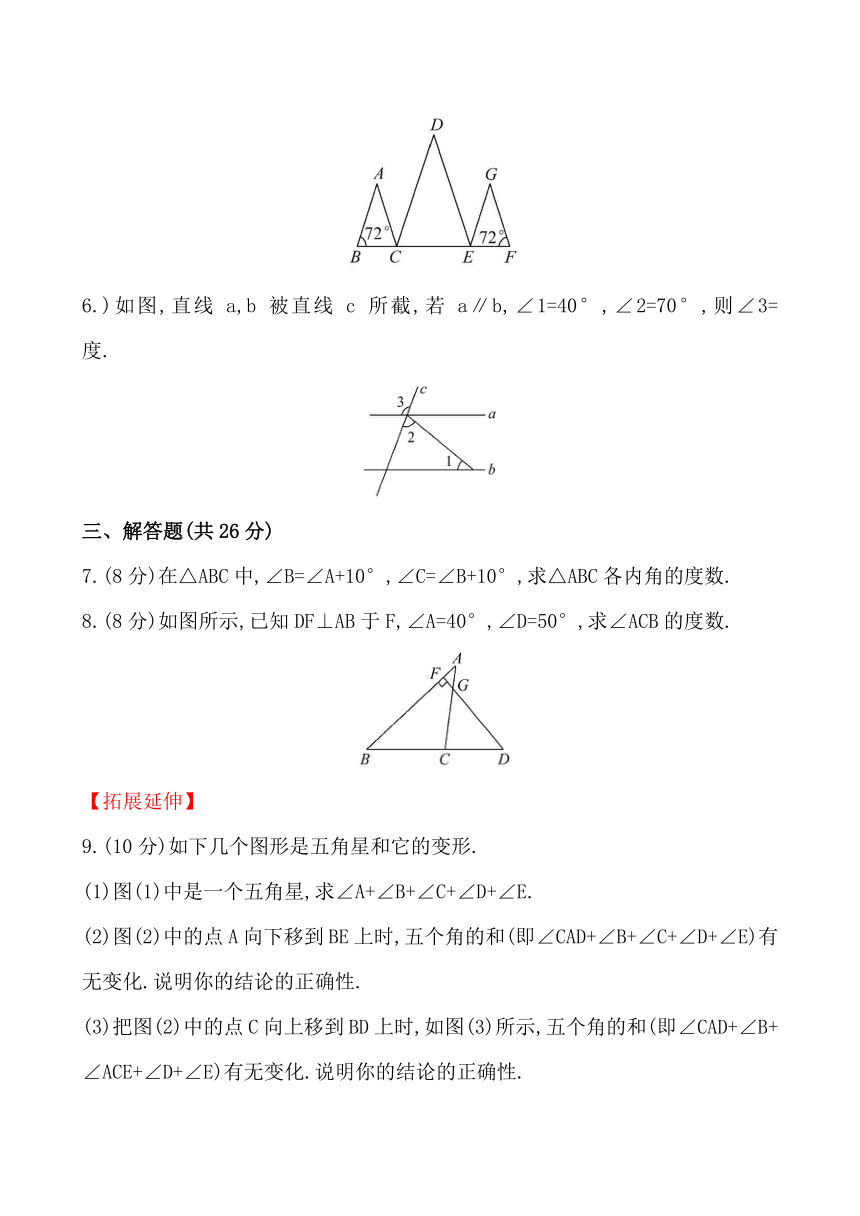
5.如图,点B,C,E,F在一直线上,AB∥DC,DE∥GF,∠B=∠F=
72°,则∠D= 度.
6.)如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3= 度.
三、解答题(共26分)
7.(8分)在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数.
8.(8分)如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数.
【拓展延伸】
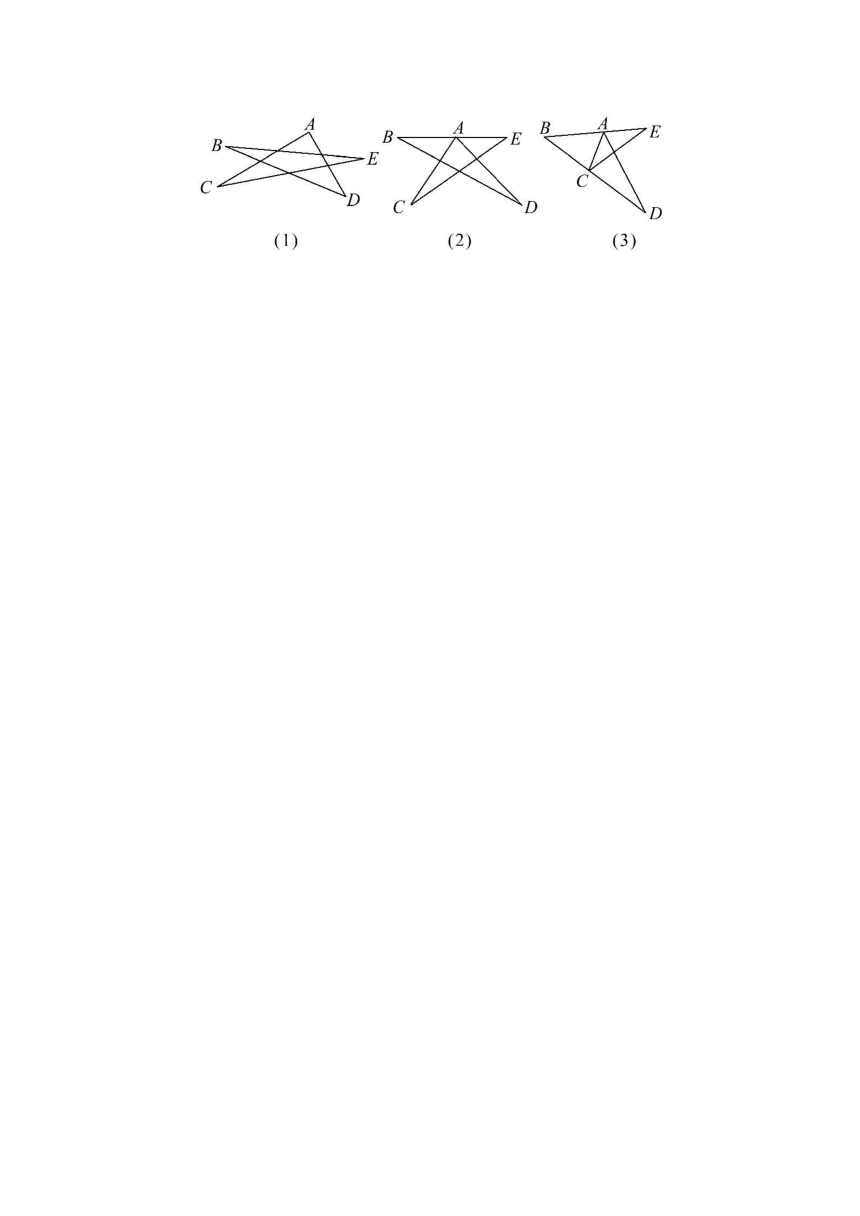
9.(10分)如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化.说明你的结论的正确性.
(3)把图(2)中的点C向上移到BD上时,如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化.说明你的结论的正确性.
答案解析
1.【解析】选A.设三个外角的度数分别是2x,3x,4x,
根据三角形的外角和为360°,得2x+3x+4x=360°,
解得x=40°,所以2x=2×40°=80°,
3x=3×40°=120°,4x=4×40°=160°.
2.【解析】选B.∠2,∠3,∠4与∠1互余.
3.【解析】选C.∵∠1是△ABC的一个外角,
∴∠1=∠A+∠C.
∴∠A=100°-70°=30°.
4.【解析】三角形的内角和为180°,
所以∠C=180°-∠A-∠B=180°-100°-40°=40°.
答案:40
5.【解析】∵AB∥DC,∴∠DCE=∠B=72°.
∵DE∥GF,∴∠DEC=∠F=72°,
∴∠D=180°-72°-72°=36°.
答案:36
6.【解析】如图,∵a∥b,∴∠3=∠4,
又∠4=∠1+∠2=110°,
∴∠3=110°.
答案:110
7.【解析】∵∠B=∠A+10°,∠C=∠B+10°,
又∵∠A+∠B+∠C=180°,
∴∠A+(∠A+10°)+(∠A+10°+10°)=180°,
3∠A+30°=180°,3∠A=150°,∠A=50°.
∴∠B=60°,∠C=70°.
8.【解析】因为∠ACB是△CDG的外角,
所以∠ACB=∠D+∠CGD.
又因为∠CGD与∠AGF为对顶角,
所以∠AGF=∠CGD.
在△AFG中,∠AGF=90°-∠A=50°.
所以∠ACB=∠D+∠AGF=100°.
9.【解析】(1)如图,连结CD.
在△ACD中,根据三角形内角和定理,
得出∠A+∠2+∠3+∠ACE+∠ADB=180°.
∵∠1=∠B+∠E=∠2+∠3,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°.
(2)无变化.
根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.∵∠BAC=∠C+∠E,∠EAD=
∠B+∠D,
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°.
(3)无变化.
根据平角的定义,得出∠ACB+∠ACE+∠ECD=180°.
∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.
一、选择题(每小题4分,共12分)
1.三角形的三个外角之比为2∶3∶4,则该三角形的三个外角分别为 ( )
A.80°,120°,160° B.40°,60°,80°
C.100°,60°,20° D.140°,120°,100°
2.直尺与三角尺按如图所示的方式叠放在一起,在图中所标记的角中,与∠1互余的角有几个 ( )
A.2个 B.3个 C.4个 D.5个
3.如图,∠1=100°,∠C=70°,则∠A的大小是 ( )
A.10° B.20° C.30° D.80°
二、填空题(每小题4分,共12分)
4.如图是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角是 度.
5.如图,点B,C,E,F在一直线上,AB∥DC,DE∥GF,∠B=∠F=
72°,则∠D= 度.
6.)如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3= 度.
三、解答题(共26分)
7.(8分)在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数.
8.(8分)如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数.
【拓展延伸】
9.(10分)如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化.说明你的结论的正确性.
(3)把图(2)中的点C向上移到BD上时,如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化.说明你的结论的正确性.
答案解析
1.【解析】选A.设三个外角的度数分别是2x,3x,4x,
根据三角形的外角和为360°,得2x+3x+4x=360°,
解得x=40°,所以2x=2×40°=80°,
3x=3×40°=120°,4x=4×40°=160°.
2.【解析】选B.∠2,∠3,∠4与∠1互余.
3.【解析】选C.∵∠1是△ABC的一个外角,
∴∠1=∠A+∠C.
∴∠A=100°-70°=30°.
4.【解析】三角形的内角和为180°,
所以∠C=180°-∠A-∠B=180°-100°-40°=40°.
答案:40
5.【解析】∵AB∥DC,∴∠DCE=∠B=72°.
∵DE∥GF,∴∠DEC=∠F=72°,
∴∠D=180°-72°-72°=36°.
答案:36
6.【解析】如图,∵a∥b,∴∠3=∠4,
又∠4=∠1+∠2=110°,
∴∠3=110°.
答案:110
7.【解析】∵∠B=∠A+10°,∠C=∠B+10°,
又∵∠A+∠B+∠C=180°,
∴∠A+(∠A+10°)+(∠A+10°+10°)=180°,
3∠A+30°=180°,3∠A=150°,∠A=50°.
∴∠B=60°,∠C=70°.
8.【解析】因为∠ACB是△CDG的外角,
所以∠ACB=∠D+∠CGD.
又因为∠CGD与∠AGF为对顶角,
所以∠AGF=∠CGD.
在△AFG中,∠AGF=90°-∠A=50°.
所以∠ACB=∠D+∠AGF=100°.
9.【解析】(1)如图,连结CD.
在△ACD中,根据三角形内角和定理,
得出∠A+∠2+∠3+∠ACE+∠ADB=180°.
∵∠1=∠B+∠E=∠2+∠3,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°.
(2)无变化.
根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.∵∠BAC=∠C+∠E,∠EAD=
∠B+∠D,
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°.
(3)无变化.
根据平角的定义,得出∠ACB+∠ACE+∠ECD=180°.
∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.
