9.1.3三角形的三边关系课时作业(含解析)
文档属性
| 名称 | 9.1.3三角形的三边关系课时作业(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 78.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 22:58:39 | ||
图片预览

文档简介
9.1.3三角形的三边关系课时作业
一、选择题(每小题4分,共12分)
1.下列每组数分别表示三根木棒的长度,将它们首尾连结后,能摆成三角形的一组是 ( )
A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4
2.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2,3,4,6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之间的最大值是 ( )
A.5 B.6 C.7 D.10
3.一个三角形的两边长分别为3和7,且第三边的边长为整数,这样的三角形的周长的最小值是 ( )
A.14 B.15 C.16 D.17
二、填空题(每小题4分,共12分)
4.工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB,CD两根木条),这样做根据的数学知识是 .
5.等腰三角形的周长为16,其一边长为6,则另两边为 .
6.若(a-1)2+|b-2|=0,则以a,b为边长的等腰三角形的周长为 .
三、解答题(共26分)
7.(8分)如果a,b,c是△ABC的三边长,请化简:|a-b-c|-|b-a+c|-|c-a-b|.
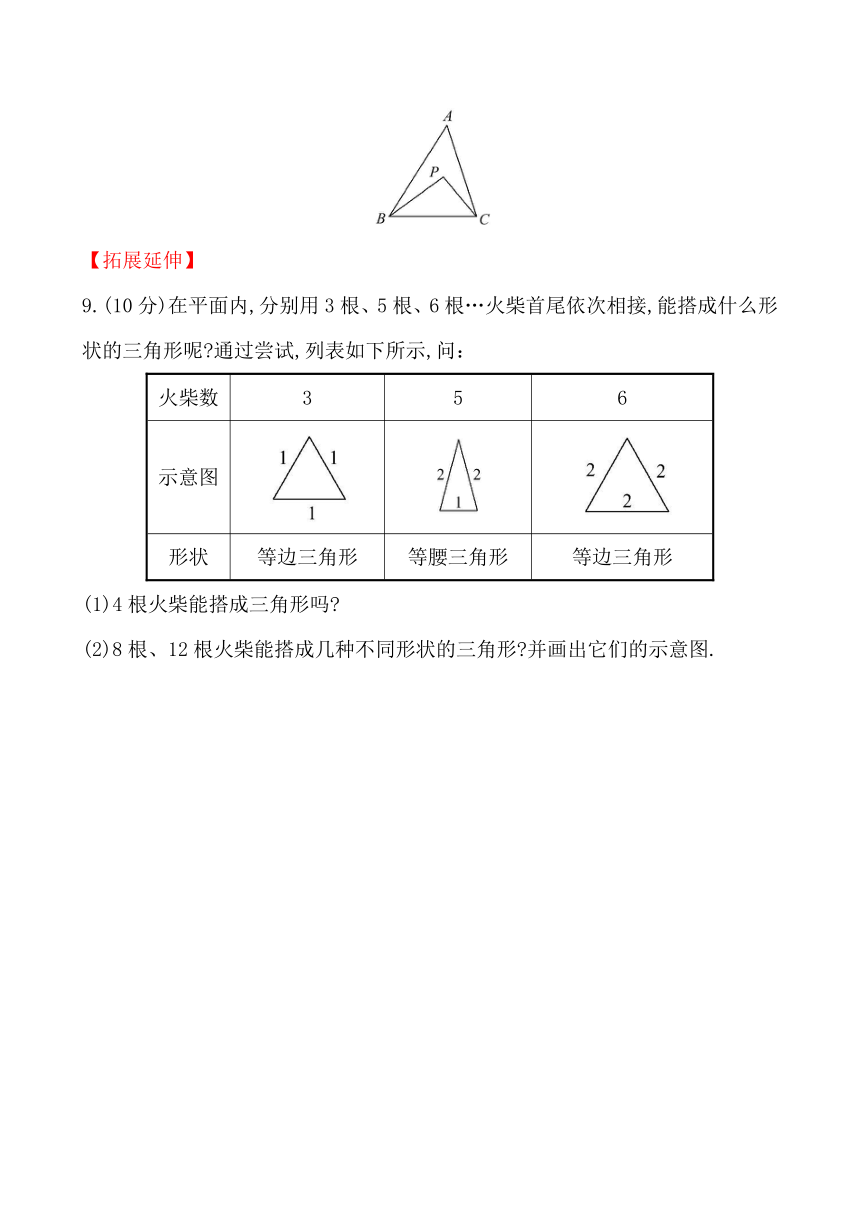
8.(8分)如图,点P是△ABC内任意一点,试说明PB+PC【拓展延伸】
9.(10分)在平面内,分别用3根、5根、6根…火柴首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下所示,问:
火柴数
3
5
6
示意图
形状
等边三角形
等腰三角形
等边三角形
(1)4根火柴能搭成三角形吗?
(2)8根、12根火柴能搭成几种不同形状的三角形?并画出它们的示意图.
答案解析
1.【解析】选D.A中因为1+2<6,所以本组数不能构成三角形;
B中因为2+2=4,所以本组数不能构成三角形;
C中因为1+2=3,所以本组数不能构成三角形;
D中因为2+3>4,所以本组数可以构成三角形.
2.【解析】选C.当把四边形调整为三角形时,两螺丝的距离可被拉大,其情况为:4,5,6和2,6,7,所以两螺丝的最大距离为7.
3.【解析】选B.设第三边的长为x,则7-3∴x可取5,6,7,8,9,
∴这个三角形的周长的最小值为15.
4.【解析】钉上两条斜拉的木条后,形成了两个三角形,这种做法根据的是三角形的稳定性.
答案:三角形的稳定性
5.【解析】当腰是6时,则另两边是4,6,且4+6>6,满足三边关系;当底边是6时,另两边长是5,5,5+5>6,
满足三边关系,故该等腰三角形的另两边长为6和4或5和5.
答案:6和4或5和5
6.【解析】由题意得a=1,b=2,组成三角形的情况为1,2,2,所以周长为5.
答案:5
7.【解析】因为a,b,c是△ABC的三边长,
所以aa-c,c|a-b-c|-|b-a+c|-|c-a-b|
=|a-(b+c)|-|b-(a-c)|-|c-(a+b)|
=(b+c)-a-[b-(a-c)]-[(a+b)-c]
=b+c-a-b+a-c-a-b+c
=c-a-b.
8.【解析】延长BP交AC于点D,
在△ABD中,PB+PD在△PCD中,PC①+②得PB+PD+PC即PB+PC9.【解析】(1)4根火柴不能搭成三角形.
(2)8根火柴能搭成一种三角形(3,3,2).
示意图:等腰三角形
12根火柴能搭成3种不同形状的三角形(4,4,4;5,5,2;3,4,5).示意图:
一、选择题(每小题4分,共12分)
1.下列每组数分别表示三根木棒的长度,将它们首尾连结后,能摆成三角形的一组是 ( )
A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4
2.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2,3,4,6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之间的最大值是 ( )
A.5 B.6 C.7 D.10
3.一个三角形的两边长分别为3和7,且第三边的边长为整数,这样的三角形的周长的最小值是 ( )
A.14 B.15 C.16 D.17
二、填空题(每小题4分,共12分)
4.工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB,CD两根木条),这样做根据的数学知识是 .
5.等腰三角形的周长为16,其一边长为6,则另两边为 .
6.若(a-1)2+|b-2|=0,则以a,b为边长的等腰三角形的周长为 .
三、解答题(共26分)
7.(8分)如果a,b,c是△ABC的三边长,请化简:|a-b-c|-|b-a+c|-|c-a-b|.
8.(8分)如图,点P是△ABC内任意一点,试说明PB+PC
9.(10分)在平面内,分别用3根、5根、6根…火柴首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下所示,问:
火柴数
3
5
6
示意图
形状
等边三角形
等腰三角形
等边三角形
(1)4根火柴能搭成三角形吗?
(2)8根、12根火柴能搭成几种不同形状的三角形?并画出它们的示意图.
答案解析
1.【解析】选D.A中因为1+2<6,所以本组数不能构成三角形;
B中因为2+2=4,所以本组数不能构成三角形;
C中因为1+2=3,所以本组数不能构成三角形;
D中因为2+3>4,所以本组数可以构成三角形.
2.【解析】选C.当把四边形调整为三角形时,两螺丝的距离可被拉大,其情况为:4,5,6和2,6,7,所以两螺丝的最大距离为7.
3.【解析】选B.设第三边的长为x,则7-3
∴这个三角形的周长的最小值为15.
4.【解析】钉上两条斜拉的木条后,形成了两个三角形,这种做法根据的是三角形的稳定性.
答案:三角形的稳定性
5.【解析】当腰是6时,则另两边是4,6,且4+6>6,满足三边关系;当底边是6时,另两边长是5,5,5+5>6,
满足三边关系,故该等腰三角形的另两边长为6和4或5和5.
答案:6和4或5和5
6.【解析】由题意得a=1,b=2,组成三角形的情况为1,2,2,所以周长为5.
答案:5
7.【解析】因为a,b,c是△ABC的三边长,
所以a
=|a-(b+c)|-|b-(a-c)|-|c-(a+b)|
=(b+c)-a-[b-(a-c)]-[(a+b)-c]
=b+c-a-b+a-c-a-b+c
=c-a-b.
8.【解析】延长BP交AC于点D,
在△ABD中,PB+PD
(2)8根火柴能搭成一种三角形(3,3,2).
示意图:等腰三角形
12根火柴能搭成3种不同形状的三角形(4,4,4;5,5,2;3,4,5).示意图:
