9.2多边形的内角和与外角和课时作业(含解析)
文档属性
| 名称 | 9.2多边形的内角和与外角和课时作业(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 22:56:40 | ||
图片预览

文档简介
9.2多边形的内角和与外角和课时作业
一、选择题(每小题4分,共12分)
1.已知一个多边形的内角和是540°,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D.七边形
2.一个多边形的每个外角都等于72°,则这个多边形的边数为
( )
A.5 B.6 C.7 D.8
3.一个多边形除了一个内角外,其余内角之和为257°,则这一内角等于( )
A.90° B.105° C.103° D.120°
二、填空题(每小题4分,共12分)
4.正八边形的一个内角的度数是 度.
5.如图,一束平行太阳光线照射到正五边形上,则∠1=
°.
6.如图是一个五角星图案,中间部分的五边形ABCDE是一个正五边形,则图中∠ABC的度数是 度.
三、解答题(共26分)
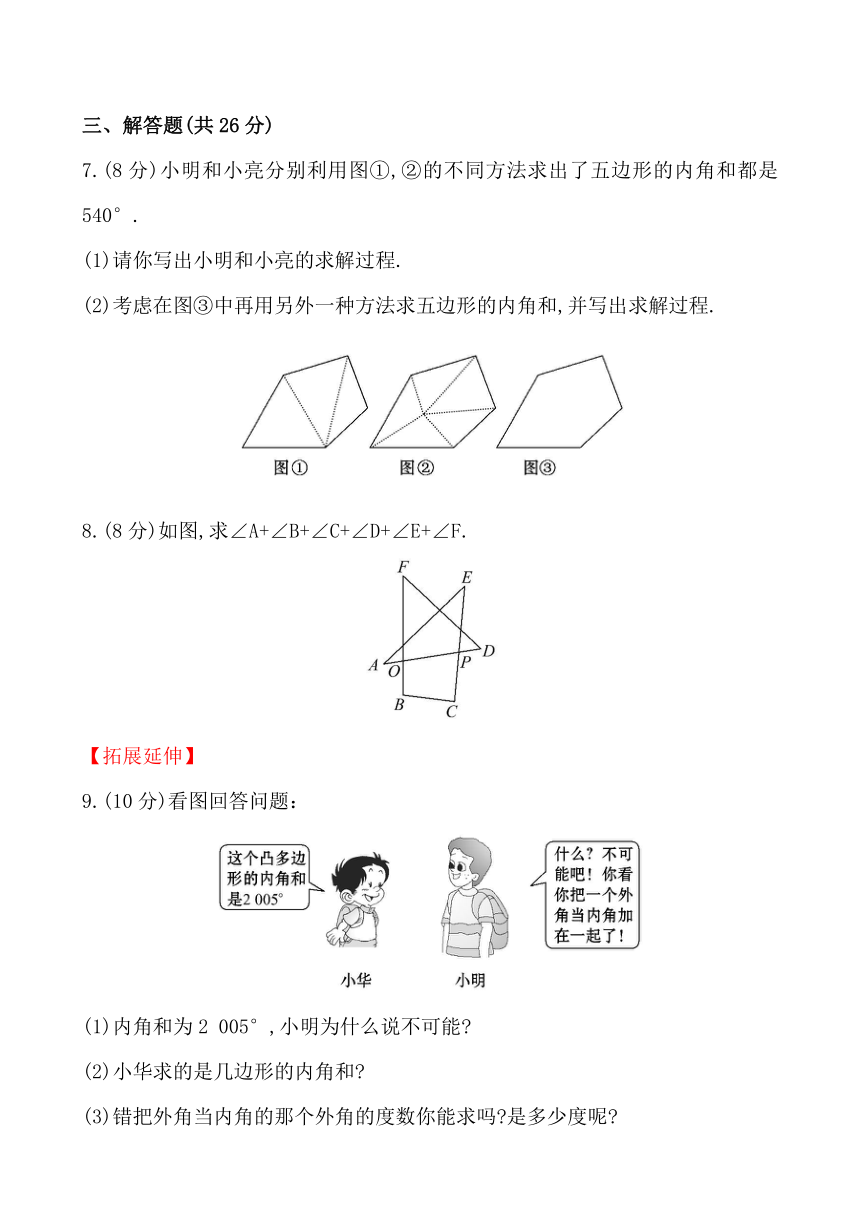
7.(8分)小明和小亮分别利用图①,②的不同方法求出了五边形的内角和都是540°.
(1)请你写出小明和小亮的求解过程.
(2)考虑在图③中再用另外一种方法求五边形的内角和,并写出求解过程.
8.(8分)如图,求∠A+∠B+∠C+∠D+∠E+∠F.
【拓展延伸】
9.(10分)看图回答问题:
(1)内角和为2 005°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求吗?是多少度呢?
答案解析
1.【解析】选B.设这个多边形的边数为n,
则:180°·(n-2)=540°,解得:n=5.
2.【解析】选A.=5.
3.【解析】选C.设多边形的边数是n,
则(n-2)·180°>257°>(n-3)·180°,
解得3则多边形的边数是4,
因为四边形的内角和是360°,
所以这一内角等于360°-257°=103°.
4.【解析】由多边形内角和定理可得,=135°.
答案:135
5.【解析】如图,延长正五边形的一边,
因为光线平行,则∠3=42°,正五边形的每个外角为360°÷5=72°,所以∠1=
72°-∠3=30°.
答案:30
6.【解析】∵ABCDE是一个正五边形,
∴五边形的内角和是(5-2)×180°=540°,
∴∠ABC=540°÷5=108°.
答案:108
7.【解析】(1)小明的解法:(5-2)×180°=540°,
小亮的解法:5×180°-360°=540°.
(2)如图,在一边上任找一点,与其他端点连结,共得到四个三角形,五边形的内角和为:4×180°-180°=540°.
8.【解析】∵∠APC是△AEP的外角,∴∠APC=∠A+∠E.∵∠BOD是△DOF的外角,∴∠BOD=∠D+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F=∠B+∠C+∠APC+∠BOD=180°×(4-2)=360°.
9.【解析】(1)∵2 005°不是180°的整数倍,
∴小明说不可能.
(2)依题意有(x-2)·180=2 005,
解得x≈13.138 9.
因而多边形的边数是13,该多边形为十三边形.
(3)13边形的内角和是(13-2)×180°=1 980°,
则错把外角当内角的那个外角的度数是2 005°-1 980°=25°.
一、选择题(每小题4分,共12分)
1.已知一个多边形的内角和是540°,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D.七边形
2.一个多边形的每个外角都等于72°,则这个多边形的边数为
( )
A.5 B.6 C.7 D.8
3.一个多边形除了一个内角外,其余内角之和为257°,则这一内角等于( )
A.90° B.105° C.103° D.120°
二、填空题(每小题4分,共12分)
4.正八边形的一个内角的度数是 度.
5.如图,一束平行太阳光线照射到正五边形上,则∠1=
°.
6.如图是一个五角星图案,中间部分的五边形ABCDE是一个正五边形,则图中∠ABC的度数是 度.
三、解答题(共26分)
7.(8分)小明和小亮分别利用图①,②的不同方法求出了五边形的内角和都是540°.
(1)请你写出小明和小亮的求解过程.
(2)考虑在图③中再用另外一种方法求五边形的内角和,并写出求解过程.
8.(8分)如图,求∠A+∠B+∠C+∠D+∠E+∠F.
【拓展延伸】
9.(10分)看图回答问题:
(1)内角和为2 005°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求吗?是多少度呢?
答案解析
1.【解析】选B.设这个多边形的边数为n,
则:180°·(n-2)=540°,解得:n=5.
2.【解析】选A.=5.
3.【解析】选C.设多边形的边数是n,
则(n-2)·180°>257°>(n-3)·180°,
解得3
因为四边形的内角和是360°,
所以这一内角等于360°-257°=103°.
4.【解析】由多边形内角和定理可得,=135°.
答案:135
5.【解析】如图,延长正五边形的一边,
因为光线平行,则∠3=42°,正五边形的每个外角为360°÷5=72°,所以∠1=
72°-∠3=30°.
答案:30
6.【解析】∵ABCDE是一个正五边形,
∴五边形的内角和是(5-2)×180°=540°,
∴∠ABC=540°÷5=108°.
答案:108
7.【解析】(1)小明的解法:(5-2)×180°=540°,
小亮的解法:5×180°-360°=540°.
(2)如图,在一边上任找一点,与其他端点连结,共得到四个三角形,五边形的内角和为:4×180°-180°=540°.
8.【解析】∵∠APC是△AEP的外角,∴∠APC=∠A+∠E.∵∠BOD是△DOF的外角,∴∠BOD=∠D+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F=∠B+∠C+∠APC+∠BOD=180°×(4-2)=360°.
9.【解析】(1)∵2 005°不是180°的整数倍,
∴小明说不可能.
(2)依题意有(x-2)·180=2 005,
解得x≈13.138 9.
因而多边形的边数是13,该多边形为十三边形.
(3)13边形的内角和是(13-2)×180°=1 980°,
则错把外角当内角的那个外角的度数是2 005°-1 980°=25°.
