北师大版数学八年级上册 2024-2025学年八年级数学上册第三章 位置与坐标 综合测试卷(含答案)
文档属性
| 名称 | 北师大版数学八年级上册 2024-2025学年八年级数学上册第三章 位置与坐标 综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览




文档简介
第三章综合测试卷
考试时间:120分钟 满分:120分
题号 — 二 三 总分
得分
一、选择题
1.如果3a<0,则点A(a,3)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
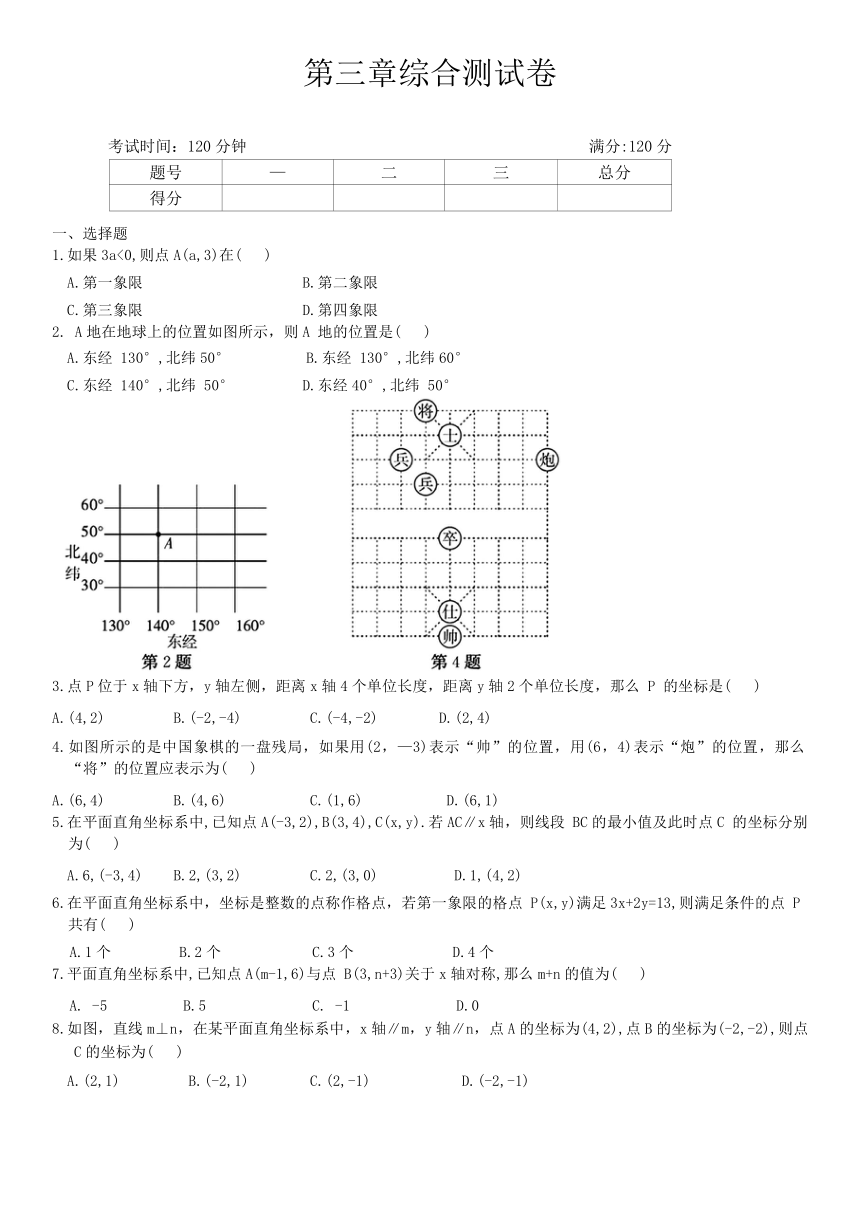
2. A地在地球上的位置如图所示,则A 地的位置是( )
A.东经 130°,北纬50° B.东经 130°,北纬60°
C.东经 140°,北纬 50° D.东经40°,北纬 50°
3.点P位于x轴下方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度,那么 P 的坐标是( )
A.(4,2) B.(-2,-4) C.(-4,-2) D.(2,4)
4.如图所示的是中国象棋的一盘残局,如果用(2,—3)表示“帅”的位置,用(6,4)表示“炮”的位置,那么“将”的位置应表示为( )
A.(6,4) B.(4,6) C.(1,6) D.(6,1)
5.在平面直角坐标系中,已知点A(-3,2),B(3,4),C(x,y).若AC∥x轴,则线段 BC的最小值及此时点C 的坐标分别为( )
A.6,(-3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
6.在平面直角坐标系中,坐标是整数的点称作格点,若第一象限的格点 P(x,y)满足3x+2y=13,则满足条件的点 P 共有( )
A.1个 B.2个 C.3个 D.4个
7.平面直角坐标系中,已知点A(m-1,6)与点 B(3,n+3)关于x轴对称,那么m+n的值为( )
A. -5 B.5 C. -1 D.0
8.如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(4,2),点B的坐标为(-2,-2),则点 C的坐标为( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
9.若m为任意实数,则点 P(m-2,m+3)一定不在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
10.如图,在平面直角坐标系中,点P (-1,0),P (-1,-1),P (1,-1),P (1,1),P (-2,1),P (-2,-2),…,,按此规律继续下去,则 P 的坐标为( )
A.(505,-505) B.(-505,505)
C.(-505,504) D.(-506,505)
二、填空题
11.一只蚂蚁由(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是 .
12.在平面直角坐标系内,已知点Q(m+3,2m+4)在x轴上,则m的值为 ,点Q的坐标为 .
13.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标 是 .
14.已知点A(a,0)和点 B(0,5)两点,且直线AB 与坐标轴围成的三角形的面积等于10,则a的值是 .
三、解答题
15.(本题满分5分)西西利用假期参观了某生态果树种植基地,他出发沿(5,—3),(5,0),(5,4),(1,3),(-3,3), (-4,0),(-4,-3),(2,-2)的路线进行了参观,写出他路上经过的地方,并用线段依次连接他经过的地点.
16.(本题满分5分)某市有A,B,C,D四个大型超市,分别位于一条东西走向的平安大路两侧.如图,若
C(-2,8),D(0,0),请建立适当的直角坐标系,并写出A,B两个超市相应的坐标.
17.(本题满分5分)如图,在正三角形ABC中,A(-4,0),B(2,0),AB=6.求点C的坐标.
18.(本题满分5分)将一组数、 按下列方式进行排列:
…
若2的位置记为(1,2),的位置记为(2,1),用数对表示这个数的位置.
19.(本题满分7分)如图,已知四边形ABCD,网格中每个小正方形的边长均为1.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
20.(本题满分7分)在如图所示的平面直角坐标系中描出下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7).
(1)A点到原点O 的距离是 个单位长度;
(2)将点C向左平移6个单位长度,它会与点 重合;
(3)作直线CE,则直线CE与y轴是什么位置关系
(4)点F到x轴、y轴的距离分别是多少
21.(本题满分7分)如图:
(1)写出A,B,C三点的坐标;
(2)若 各顶点的横坐标不变,纵坐标都乘 ,请你在同一坐标系中描出对应的点 ,并依次连接这三个点,所得的 与原 有怎样的位置关系.
22.(本题满分7分)已知点.
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求 的值.
23.(本题满分8分)如图,点A(-1,0),C(1,4),点B在x轴上,且.
(1)求点 B 的坐标.
(2)求 的面积.
(3)在y轴上是否存在点 P,使以A,B,P三点为顶点的三角形的面积为7 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
(本题满分10分)如图,在长方形OABC中,O为平面直角坐标系的原点,点A 的坐标为(a,0),点C的坐标为 (0,b),且 ab满足 点B在第一象限内,点P 从原点出发,以每秒2个单位长度的速度
沿着 的线路移动.
点B 的坐标为 ;
(2)当点 P 移动4秒时,请指出点 P 的位置,并求出点 P 的坐标;
(3)在移动过程中,当点 P到x轴的距离为5个单位长度时,求点 P移动的时间.
25.(本题满分12分)如图,在平面直角坐标系中,A,B,C三点的坐标分别为(0,1),(2,0),(2,1.5).
(1)求 的面积.
(2)如果在第二象限内有一点 ,试用含a的式子表示四边形ABOP 的面积.
(3)在(2)的条件下,是否存在点 P,使得四边形 ABOP 的面积与 的面积相等 若存在,请求出点 P 的坐标;若不存在,请说明理由.
第三章综合测试卷
1.B 2.C 3.B 4.C 5.B 6.B 7.A 8.C 9.D 10.D
11. (3,2) 12. —2 ,(1,0) 13. (-2,2) 14. ±4 .
15.解:如图所示,他依次经过枣林、梨园、苹果园、葡萄园、杏林、桃林、梅林、山楂林.
16.解:建立如图所示的直角坐标系.点A 的坐标为(10,9),点B的坐标为(6,-1).
17.解:过C作CD⊥x轴,垂足为D.
因为AC=BC=AB,
所以由作图得
所以D(-1,0).在Rt△ACD 中,
所以
18.解:按规律排列知, 位于第4行,第4列,所以它的位置记为(4,4).
19.解:(1)由图象可知点A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)作AE⊥BC 于点E,DF⊥BC 于点 F,
则 4)×3=16.
20.(1)A点到原点O 的距离是 3 个单位长度;
(2)将点C向左平移6个单位长度,它会与点 D 重合;
解:各点的位置如图所示.
直线CE 如图所示,因为C(3,-5),E(3,5),
即C与E 的横坐标相同,
所以直线 CE 平行于y轴.
(4)因为F(5,7),所以点 F到x 轴、y 轴的距离分别是7、5.
21.解:(1)A(3,4) B(1,2) C(5,1)
(2)如图,△A'B'C'与△ABC 关于 x 轴对称.
22.解:(1)由题意知,2a-b=2b-1,5+a-a+b=0,解得b=-5,a=-8.
(2)由题意知:2a-b+2b--1=0,5+a=-a+b,所以 2a=b-5,所以1-b=b-5,b=3,a=-1.
则
23.解:(1)点 B 的坐标为(--5,0)或(3,0).
(2)因为点 C(1,4),AB=4,
所以 8.
(3)在 y 轴上存在点 或
使以A,B,P三点为顶点的三角形的面积为7.
24.(1)a= 4 ,b= 6 ,点 B 的坐标为 (4,6) ;
解:(2)当点 P移动4秒时,在线段CB 的中点处,点P 的坐标是(2,6).
(3)由题意可得,在移动过程中,当点P到x 轴的距离为5个单位长度时,存在两种情况.第一种情况,
当点 P 在OC 上时,点P 移动的时间是5÷2=2.5秒;
第二种情况,当点P 在BA上时,点P移动的时间是(6+4+1)÷2=5.5秒,
所以点P移动的时i是2.5秒或5.5秒.
25.解:(1)由点B(2,0),C(2,1.5)可知CB⊥x 轴.
如图,过点A 作AD⊥BC,垂足为D,
则 1.5.
(2)如图,过点 P 作PE⊥y轴,垂足为E,
则
(3)存在这样的点 P.依题意,有 解得a=-1.所以点P 的坐标为
考试时间:120分钟 满分:120分
题号 — 二 三 总分
得分
一、选择题
1.如果3a<0,则点A(a,3)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2. A地在地球上的位置如图所示,则A 地的位置是( )
A.东经 130°,北纬50° B.东经 130°,北纬60°
C.东经 140°,北纬 50° D.东经40°,北纬 50°
3.点P位于x轴下方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度,那么 P 的坐标是( )
A.(4,2) B.(-2,-4) C.(-4,-2) D.(2,4)
4.如图所示的是中国象棋的一盘残局,如果用(2,—3)表示“帅”的位置,用(6,4)表示“炮”的位置,那么“将”的位置应表示为( )
A.(6,4) B.(4,6) C.(1,6) D.(6,1)
5.在平面直角坐标系中,已知点A(-3,2),B(3,4),C(x,y).若AC∥x轴,则线段 BC的最小值及此时点C 的坐标分别为( )
A.6,(-3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
6.在平面直角坐标系中,坐标是整数的点称作格点,若第一象限的格点 P(x,y)满足3x+2y=13,则满足条件的点 P 共有( )
A.1个 B.2个 C.3个 D.4个
7.平面直角坐标系中,已知点A(m-1,6)与点 B(3,n+3)关于x轴对称,那么m+n的值为( )
A. -5 B.5 C. -1 D.0
8.如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(4,2),点B的坐标为(-2,-2),则点 C的坐标为( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
9.若m为任意实数,则点 P(m-2,m+3)一定不在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
10.如图,在平面直角坐标系中,点P (-1,0),P (-1,-1),P (1,-1),P (1,1),P (-2,1),P (-2,-2),…,,按此规律继续下去,则 P 的坐标为( )
A.(505,-505) B.(-505,505)
C.(-505,504) D.(-506,505)
二、填空题
11.一只蚂蚁由(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是 .
12.在平面直角坐标系内,已知点Q(m+3,2m+4)在x轴上,则m的值为 ,点Q的坐标为 .
13.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标 是 .
14.已知点A(a,0)和点 B(0,5)两点,且直线AB 与坐标轴围成的三角形的面积等于10,则a的值是 .
三、解答题
15.(本题满分5分)西西利用假期参观了某生态果树种植基地,他出发沿(5,—3),(5,0),(5,4),(1,3),(-3,3), (-4,0),(-4,-3),(2,-2)的路线进行了参观,写出他路上经过的地方,并用线段依次连接他经过的地点.
16.(本题满分5分)某市有A,B,C,D四个大型超市,分别位于一条东西走向的平安大路两侧.如图,若
C(-2,8),D(0,0),请建立适当的直角坐标系,并写出A,B两个超市相应的坐标.
17.(本题满分5分)如图,在正三角形ABC中,A(-4,0),B(2,0),AB=6.求点C的坐标.
18.(本题满分5分)将一组数、 按下列方式进行排列:
…
若2的位置记为(1,2),的位置记为(2,1),用数对表示这个数的位置.
19.(本题满分7分)如图,已知四边形ABCD,网格中每个小正方形的边长均为1.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
20.(本题满分7分)在如图所示的平面直角坐标系中描出下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7).
(1)A点到原点O 的距离是 个单位长度;
(2)将点C向左平移6个单位长度,它会与点 重合;
(3)作直线CE,则直线CE与y轴是什么位置关系
(4)点F到x轴、y轴的距离分别是多少
21.(本题满分7分)如图:
(1)写出A,B,C三点的坐标;
(2)若 各顶点的横坐标不变,纵坐标都乘 ,请你在同一坐标系中描出对应的点 ,并依次连接这三个点,所得的 与原 有怎样的位置关系.
22.(本题满分7分)已知点.
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求 的值.
23.(本题满分8分)如图,点A(-1,0),C(1,4),点B在x轴上,且.
(1)求点 B 的坐标.
(2)求 的面积.
(3)在y轴上是否存在点 P,使以A,B,P三点为顶点的三角形的面积为7 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
(本题满分10分)如图,在长方形OABC中,O为平面直角坐标系的原点,点A 的坐标为(a,0),点C的坐标为 (0,b),且 ab满足 点B在第一象限内,点P 从原点出发,以每秒2个单位长度的速度
沿着 的线路移动.
点B 的坐标为 ;
(2)当点 P 移动4秒时,请指出点 P 的位置,并求出点 P 的坐标;
(3)在移动过程中,当点 P到x轴的距离为5个单位长度时,求点 P移动的时间.
25.(本题满分12分)如图,在平面直角坐标系中,A,B,C三点的坐标分别为(0,1),(2,0),(2,1.5).
(1)求 的面积.
(2)如果在第二象限内有一点 ,试用含a的式子表示四边形ABOP 的面积.
(3)在(2)的条件下,是否存在点 P,使得四边形 ABOP 的面积与 的面积相等 若存在,请求出点 P 的坐标;若不存在,请说明理由.
第三章综合测试卷
1.B 2.C 3.B 4.C 5.B 6.B 7.A 8.C 9.D 10.D
11. (3,2) 12. —2 ,(1,0) 13. (-2,2) 14. ±4 .
15.解:如图所示,他依次经过枣林、梨园、苹果园、葡萄园、杏林、桃林、梅林、山楂林.
16.解:建立如图所示的直角坐标系.点A 的坐标为(10,9),点B的坐标为(6,-1).
17.解:过C作CD⊥x轴,垂足为D.
因为AC=BC=AB,
所以由作图得
所以D(-1,0).在Rt△ACD 中,
所以
18.解:按规律排列知, 位于第4行,第4列,所以它的位置记为(4,4).
19.解:(1)由图象可知点A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)作AE⊥BC 于点E,DF⊥BC 于点 F,
则 4)×3=16.
20.(1)A点到原点O 的距离是 3 个单位长度;
(2)将点C向左平移6个单位长度,它会与点 D 重合;
解:各点的位置如图所示.
直线CE 如图所示,因为C(3,-5),E(3,5),
即C与E 的横坐标相同,
所以直线 CE 平行于y轴.
(4)因为F(5,7),所以点 F到x 轴、y 轴的距离分别是7、5.
21.解:(1)A(3,4) B(1,2) C(5,1)
(2)如图,△A'B'C'与△ABC 关于 x 轴对称.
22.解:(1)由题意知,2a-b=2b-1,5+a-a+b=0,解得b=-5,a=-8.
(2)由题意知:2a-b+2b--1=0,5+a=-a+b,所以 2a=b-5,所以1-b=b-5,b=3,a=-1.
则
23.解:(1)点 B 的坐标为(--5,0)或(3,0).
(2)因为点 C(1,4),AB=4,
所以 8.
(3)在 y 轴上存在点 或
使以A,B,P三点为顶点的三角形的面积为7.
24.(1)a= 4 ,b= 6 ,点 B 的坐标为 (4,6) ;
解:(2)当点 P移动4秒时,在线段CB 的中点处,点P 的坐标是(2,6).
(3)由题意可得,在移动过程中,当点P到x 轴的距离为5个单位长度时,存在两种情况.第一种情况,
当点 P 在OC 上时,点P 移动的时间是5÷2=2.5秒;
第二种情况,当点P 在BA上时,点P移动的时间是(6+4+1)÷2=5.5秒,
所以点P移动的时i是2.5秒或5.5秒.
25.解:(1)由点B(2,0),C(2,1.5)可知CB⊥x 轴.
如图,过点A 作AD⊥BC,垂足为D,
则 1.5.
(2)如图,过点 P 作PE⊥y轴,垂足为E,
则
(3)存在这样的点 P.依题意,有 解得a=-1.所以点P 的坐标为
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
