北师大版数学八年级上册 2024-2025学年八年级数学上册第四章 一次函数 测试卷(含答案)
文档属性
| 名称 | 北师大版数学八年级上册 2024-2025学年八年级数学上册第四章 一次函数 测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 586.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
第四章测试卷
题号 一 二 三 总分
得分
考试时间:45分钟 满分:100分
一、选择题
1.要使函数是一次函数,则m,n应满足( )
A. m≠2,n≠2 B. m=2,n=2
C. m≠2,n=2 D. m=2,n=1
2.下面不在函数y=-2x+3图象上的点是( )
A.(-5,13) B.(0.5,2) C.(3,0) D.(1,1)
3.某山山脚的气温是10℃,此山高度每上升 1km,气温下降6℃,设比山脚高出 xkm处的气温为y℃,则y关于x的函数表达式为( )
A. y=10--6x B. y=10+6x
C. y=6--10x D. y=6x--10
4.如图,直线y= ax+b过点A(0,2)和点 B(--3,0),则方程 ax+b=0的解是( )
A. x=2 B. x=0
C. x=--1 D. x=--3
5.去年年初以来,红星消毒液公司生产的消毒液在库存量为m 吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示去年年初至脱销期间,该厂库存量y(吨)与时间t(天)之间函数关系的大致图象的是( )
6.若直线y= kx--b沿y轴平移3个单位长度得到直线y= kx--1,则b的值为( )
A.-2或4 B.2或-4 C.4或-6 D.-4或6
7.一次函数y=-3x+1的图象过点( 则( )
8.在一次函数 中,y随x的增大而减小,则其图象可能是 ( )
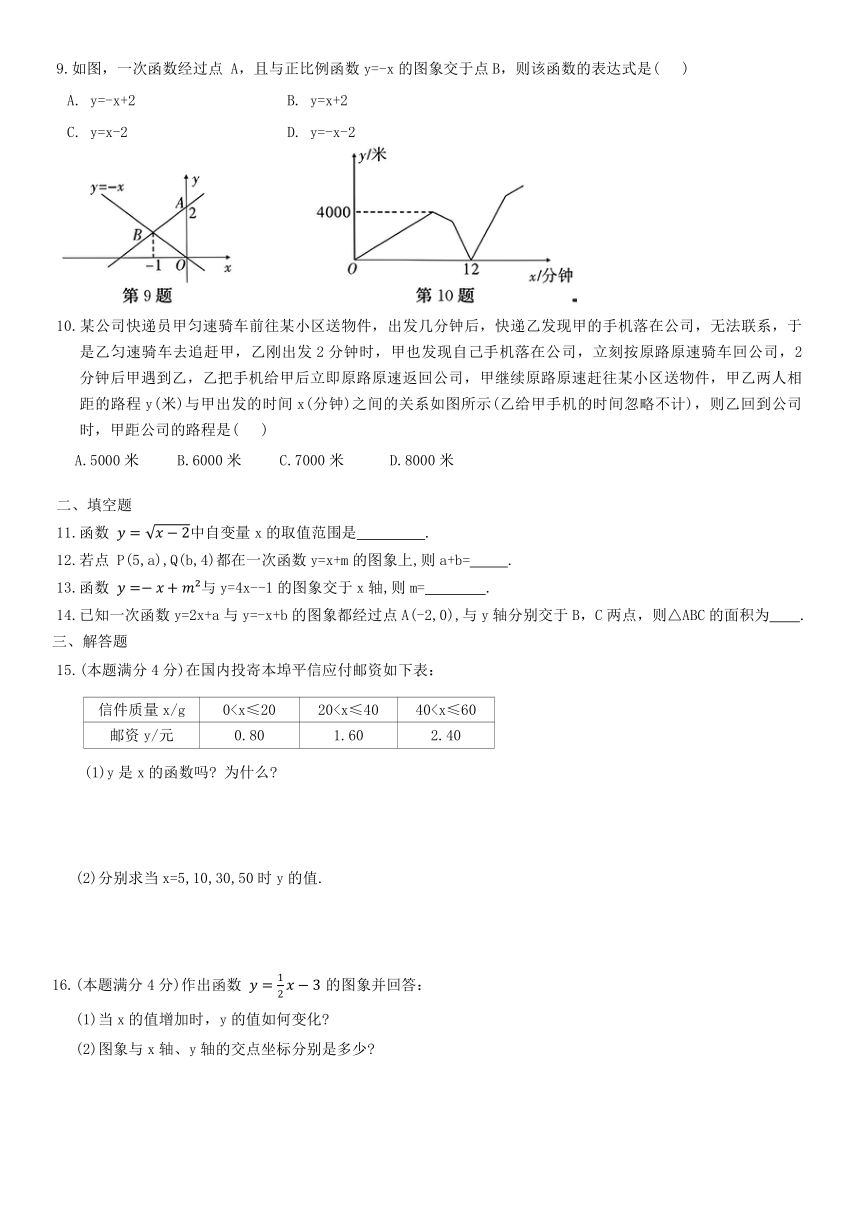
9.如图,一次函数经过点 A,且与正比例函数y=-x的图象交于点B,则该函数的表达式是( )
A. y=-x+2 B. y=x+2
C. y=x-2 D. y=-x-2
10.某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲,乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计),则乙回到公司时,甲距公司的路程是( )
A.5000米 B.6000米 C.7000米 D.8000米
二、填空题
11.函数 中自变量x的取值范围是 .
12.若点 P(5,a),Q(b,4)都在一次函数y=x+m的图象上,则a+b= .
13.函数 与y=4x--1的图象交于x轴,则m= .
14.已知一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0),与y轴分别交于B,C两点,则△ABC的面积为 .
三、解答题
15.(本题满分4分)在国内投寄本埠平信应付邮资如下表:
信件质量x/g 0邮资y/元 0.80 1.60 2.40
(1)y是x的函数吗 为什么
(2)分别求当x=5,10,30,50时y的值.
16.(本题满分4分)作出函数 的图象并回答:
(1)当x的值增加时,y的值如何变化
(2)图象与x轴、y轴的交点坐标分别是多少
17.(本题满分4分)已知一次函数 求:
(1)当k为何值时,它的图象过原点;
(2)当k为何值时,y随x的增大而减小.
18.(本题满分4分)已知y与成正比例,且时,
(1)求y与x之间的函数关系式;
(2)设点 P(a,4)在(1)中函数的图象上,求点 P 的坐标.
19.(本题满分6分)从甲地到乙地的公路长约240km,骑自行车以每小时20km的速度从甲地出发, th后离乙地skm.
(1)写出s与t 的函数表达式.
(2)8h后距乙地多远 出发后几小时,到两地的距离相等
20.(本题满分6分)如图,一次函数y=-x+5的图象与x轴交于点A,与正比例函数的图象交于点 B.若△AOB 的面积为 10,求直线OB的函数表达式.
21.(本题满分6分)某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克;若一次购买超过5千克,则超过5千克部分的种子价格打8折,设一次购买量为x千克时,付款金额为y元.
(1)求y关于x的函数表达式;
(2)若某农户一次购买玉米种子30千克,则需付款多少元
22.(本题满分6分)在平面直角坐标系xOy中,一次函数. 0)的图象由函数. 的图象平移得到,且经过点(1,2).
(1)求这个一次函数的表达式;
(2)当 时,对于x的每一个值,函数 的值大于一次函数 的值,直接写出m的取值范围.
23.(本题满分7分)定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的长方形的周长与面积在数量上相等,则这个点叫和谐点.
(1)判断点 是否为和谐点
(2)若和谐点 P(a,3)在直线. (b为常数)上,试求a,b的值.
24.(本题满分9分)雯雯家与文具店相距960m,雯雯从家出发,沿笔直的公路匀速步行12min来到文具店买笔记本,停留3min,因家中有事,便沿着原路匀速跑步6min返回家中.
(1)雯雯返回家中的速度比去文具店的速度快多少
(2)请你画出这个过程中,雯雯离家的距离y与时间x的函数图象;
(3)根据图象回答:雯雯从家出发多长时间后,离家距离为720m
25.(本题满分12分)暑期,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y (元),且 ;按照方案二所需费用为. (元),且 其函数图象如图所示.
(1)求 和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和 的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,选择哪种方案所需费用更少 说明理由.
第四章测试卷
C 2.C 3.A 4.D 5.D 6.A 7.B 8.B 9.B 10.B
x2 12. 9 13.14. 6
15.(1)解:y是x 的函数,理由:当x取一定值时,y都有唯一确定的值与其对应.
(2)解:x=5时,y=0.80;x=10时,y=0.80;x=30时,y=1.60;x=50时,y=2.40.
16.解:函数图象如图所示;
(1)当x 的值增加时,y的值随之增加.
(2)根据图象知与x轴的交点为(6,0),与y轴的交点为(0,-3).
17.解:(1)若图象过原点,则
(2)若y随x的增大而减小,则3-k<0,即k>3.
18.解:(1)设y与x之间的函数关系式为y=k(x+1)(k≠0),
将(-2,2)代入y=k(x+1),得2=k(-2+1),
解得k=-2,
所以y与x之间的函数关系式为y=-2(x+1),
即y=-2x-2.
(2)将(a,4)代入y=-2x-2,得-2a-2=4,
解得a=-3,
所以点P的坐标为(-3,4).
19.解:(1)s=240-20t(0≤t≤12)
(2)t=8时,s=80;当240-20t=20t时,t=6.即8h后距乙地80km;出发后6小时,到两地的距离相等.
20.解:因为一次函数y=-x+5的图象与x轴交于点A,
则点A 的坐标为(5,0),
所以OA=5.设点B(x,y),
因为△AOB 的面积为10,
所以 ·y=10,即
解得 y=4.
因为点 B在y=-x+5的图象上,
所以4=-x+5,
解得x=1.
所以点B的坐标为(1,4).
设直线OB 的函数表达式为y= kx(k≠0),
把点B(1,4)的坐标代入y= kx,得4=k·1,
解得k=4.所以直线OB 的函数表达式为y=4x.
21.解:(1)根据题意,得①当0≤x≤5时,y=20x;
②当x>5时,y=20×0.8(x-5)+20×5=16x+20.
(2)把x=30代入y=16x+20,得y=16×30+20=500,
所以若该农户一次购买玉米种子30千克,
则需付款500 元.
22.解:(1)因为一次函数y= kx+b(k≠0)的图象是由函数y=x的图象平移得到的,
所以k=1.将点(1,2)代入y=x+b,得2=1+b,
解得b=1,
所以一次函数的表达式为y=x+1.
(2)m≥2.
23.解:(1)因为1×2≠2×(1+2),4×4=2×(4+4),
所以点M不是和谐点,点N是和谐点.
(2)①当a>0时,(a+3)×2=3a,a=6,
因为点(a,3)在直线y=-x+b上,
所以3=-6+b,b=9.
②当a<0时,(-a+3)×2=-3a,a=-6.
因为点(a,3)在直线y=-x+b上,
所以3=6+b,b=-3,
综上a=6,b=9或a=-6,b=-3.
24.解:(1)由题意可得,雯雯返回家中的速度比去文具店的速度快
(2)如图所示.
(3)由图象可知,小慧从家出发9min后,离家距离为720m,小慧返回时的速度为960÷6=160m/min,
则小慧从家出发(960-720)÷160+15=16.5( min)后,
离家距离也为720m.综上,小慧从家出发9min或16.5min后,离家距离为720m.
25.解:(1)因为 的图象过点(0,30)和点(10,180),
所以
所以 的实际意义是:打六折后的每次健身费用为 15元.
b的实际意义是:每张学生暑期专享卡的价格为30 元.
(2)打折前的每次健身费用为15÷0.6=25(元).
(3)选择方案一所需费用更少.
理由:因为 15,b=30,
所以 因为
所以 当 时,15x+30=20x,
解得x=6.结合函数图象可知,小华暑期前往该俱乐部健身8次,选择方案一所需费用更少.
题号 一 二 三 总分
得分
考试时间:45分钟 满分:100分
一、选择题
1.要使函数是一次函数,则m,n应满足( )
A. m≠2,n≠2 B. m=2,n=2
C. m≠2,n=2 D. m=2,n=1
2.下面不在函数y=-2x+3图象上的点是( )
A.(-5,13) B.(0.5,2) C.(3,0) D.(1,1)
3.某山山脚的气温是10℃,此山高度每上升 1km,气温下降6℃,设比山脚高出 xkm处的气温为y℃,则y关于x的函数表达式为( )
A. y=10--6x B. y=10+6x
C. y=6--10x D. y=6x--10
4.如图,直线y= ax+b过点A(0,2)和点 B(--3,0),则方程 ax+b=0的解是( )
A. x=2 B. x=0
C. x=--1 D. x=--3
5.去年年初以来,红星消毒液公司生产的消毒液在库存量为m 吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示去年年初至脱销期间,该厂库存量y(吨)与时间t(天)之间函数关系的大致图象的是( )
6.若直线y= kx--b沿y轴平移3个单位长度得到直线y= kx--1,则b的值为( )
A.-2或4 B.2或-4 C.4或-6 D.-4或6
7.一次函数y=-3x+1的图象过点( 则( )
8.在一次函数 中,y随x的增大而减小,则其图象可能是 ( )
9.如图,一次函数经过点 A,且与正比例函数y=-x的图象交于点B,则该函数的表达式是( )
A. y=-x+2 B. y=x+2
C. y=x-2 D. y=-x-2
10.某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲,乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计),则乙回到公司时,甲距公司的路程是( )
A.5000米 B.6000米 C.7000米 D.8000米
二、填空题
11.函数 中自变量x的取值范围是 .
12.若点 P(5,a),Q(b,4)都在一次函数y=x+m的图象上,则a+b= .
13.函数 与y=4x--1的图象交于x轴,则m= .
14.已知一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0),与y轴分别交于B,C两点,则△ABC的面积为 .
三、解答题
15.(本题满分4分)在国内投寄本埠平信应付邮资如下表:
信件质量x/g 0
(1)y是x的函数吗 为什么
(2)分别求当x=5,10,30,50时y的值.
16.(本题满分4分)作出函数 的图象并回答:
(1)当x的值增加时,y的值如何变化
(2)图象与x轴、y轴的交点坐标分别是多少
17.(本题满分4分)已知一次函数 求:
(1)当k为何值时,它的图象过原点;
(2)当k为何值时,y随x的增大而减小.
18.(本题满分4分)已知y与成正比例,且时,
(1)求y与x之间的函数关系式;
(2)设点 P(a,4)在(1)中函数的图象上,求点 P 的坐标.
19.(本题满分6分)从甲地到乙地的公路长约240km,骑自行车以每小时20km的速度从甲地出发, th后离乙地skm.
(1)写出s与t 的函数表达式.
(2)8h后距乙地多远 出发后几小时,到两地的距离相等
20.(本题满分6分)如图,一次函数y=-x+5的图象与x轴交于点A,与正比例函数的图象交于点 B.若△AOB 的面积为 10,求直线OB的函数表达式.
21.(本题满分6分)某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克;若一次购买超过5千克,则超过5千克部分的种子价格打8折,设一次购买量为x千克时,付款金额为y元.
(1)求y关于x的函数表达式;
(2)若某农户一次购买玉米种子30千克,则需付款多少元
22.(本题满分6分)在平面直角坐标系xOy中,一次函数. 0)的图象由函数. 的图象平移得到,且经过点(1,2).
(1)求这个一次函数的表达式;
(2)当 时,对于x的每一个值,函数 的值大于一次函数 的值,直接写出m的取值范围.
23.(本题满分7分)定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的长方形的周长与面积在数量上相等,则这个点叫和谐点.
(1)判断点 是否为和谐点
(2)若和谐点 P(a,3)在直线. (b为常数)上,试求a,b的值.
24.(本题满分9分)雯雯家与文具店相距960m,雯雯从家出发,沿笔直的公路匀速步行12min来到文具店买笔记本,停留3min,因家中有事,便沿着原路匀速跑步6min返回家中.
(1)雯雯返回家中的速度比去文具店的速度快多少
(2)请你画出这个过程中,雯雯离家的距离y与时间x的函数图象;
(3)根据图象回答:雯雯从家出发多长时间后,离家距离为720m
25.(本题满分12分)暑期,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y (元),且 ;按照方案二所需费用为. (元),且 其函数图象如图所示.
(1)求 和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和 的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,选择哪种方案所需费用更少 说明理由.
第四章测试卷
C 2.C 3.A 4.D 5.D 6.A 7.B 8.B 9.B 10.B
x2 12. 9 13.14. 6
15.(1)解:y是x 的函数,理由:当x取一定值时,y都有唯一确定的值与其对应.
(2)解:x=5时,y=0.80;x=10时,y=0.80;x=30时,y=1.60;x=50时,y=2.40.
16.解:函数图象如图所示;
(1)当x 的值增加时,y的值随之增加.
(2)根据图象知与x轴的交点为(6,0),与y轴的交点为(0,-3).
17.解:(1)若图象过原点,则
(2)若y随x的增大而减小,则3-k<0,即k>3.
18.解:(1)设y与x之间的函数关系式为y=k(x+1)(k≠0),
将(-2,2)代入y=k(x+1),得2=k(-2+1),
解得k=-2,
所以y与x之间的函数关系式为y=-2(x+1),
即y=-2x-2.
(2)将(a,4)代入y=-2x-2,得-2a-2=4,
解得a=-3,
所以点P的坐标为(-3,4).
19.解:(1)s=240-20t(0≤t≤12)
(2)t=8时,s=80;当240-20t=20t时,t=6.即8h后距乙地80km;出发后6小时,到两地的距离相等.
20.解:因为一次函数y=-x+5的图象与x轴交于点A,
则点A 的坐标为(5,0),
所以OA=5.设点B(x,y),
因为△AOB 的面积为10,
所以 ·y=10,即
解得 y=4.
因为点 B在y=-x+5的图象上,
所以4=-x+5,
解得x=1.
所以点B的坐标为(1,4).
设直线OB 的函数表达式为y= kx(k≠0),
把点B(1,4)的坐标代入y= kx,得4=k·1,
解得k=4.所以直线OB 的函数表达式为y=4x.
21.解:(1)根据题意,得①当0≤x≤5时,y=20x;
②当x>5时,y=20×0.8(x-5)+20×5=16x+20.
(2)把x=30代入y=16x+20,得y=16×30+20=500,
所以若该农户一次购买玉米种子30千克,
则需付款500 元.
22.解:(1)因为一次函数y= kx+b(k≠0)的图象是由函数y=x的图象平移得到的,
所以k=1.将点(1,2)代入y=x+b,得2=1+b,
解得b=1,
所以一次函数的表达式为y=x+1.
(2)m≥2.
23.解:(1)因为1×2≠2×(1+2),4×4=2×(4+4),
所以点M不是和谐点,点N是和谐点.
(2)①当a>0时,(a+3)×2=3a,a=6,
因为点(a,3)在直线y=-x+b上,
所以3=-6+b,b=9.
②当a<0时,(-a+3)×2=-3a,a=-6.
因为点(a,3)在直线y=-x+b上,
所以3=6+b,b=-3,
综上a=6,b=9或a=-6,b=-3.
24.解:(1)由题意可得,雯雯返回家中的速度比去文具店的速度快
(2)如图所示.
(3)由图象可知,小慧从家出发9min后,离家距离为720m,小慧返回时的速度为960÷6=160m/min,
则小慧从家出发(960-720)÷160+15=16.5( min)后,
离家距离也为720m.综上,小慧从家出发9min或16.5min后,离家距离为720m.
25.解:(1)因为 的图象过点(0,30)和点(10,180),
所以
所以 的实际意义是:打六折后的每次健身费用为 15元.
b的实际意义是:每张学生暑期专享卡的价格为30 元.
(2)打折前的每次健身费用为15÷0.6=25(元).
(3)选择方案一所需费用更少.
理由:因为 15,b=30,
所以 因为
所以 当 时,15x+30=20x,
解得x=6.结合函数图象可知,小华暑期前往该俱乐部健身8次,选择方案一所需费用更少.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
