10.3.1图形的旋转课时作业(含解析)
文档属性
| 名称 | 10.3.1图形的旋转课时作业(含解析) | 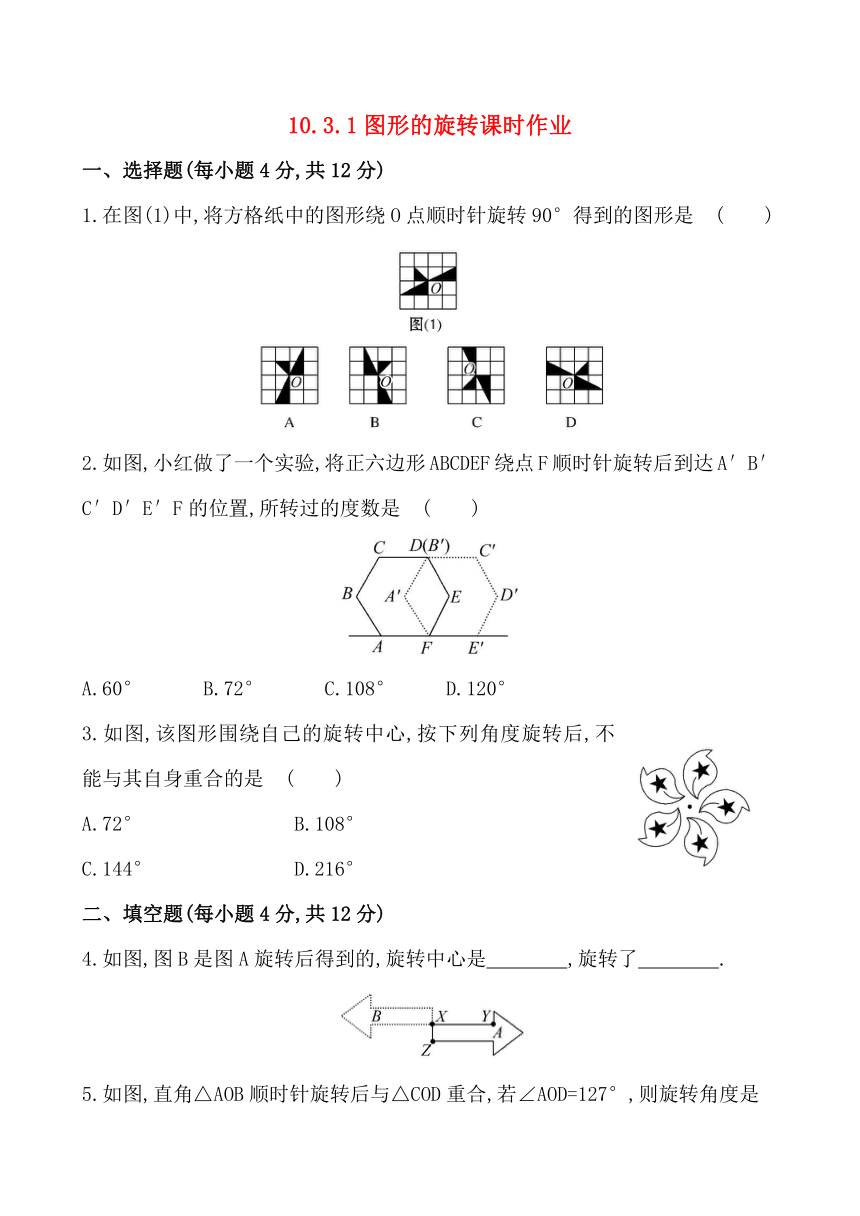 | |
| 格式 | zip | ||
| 文件大小 | 133.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 22:49:13 | ||
图片预览


文档简介
10.3.1图形的旋转课时作业
一、选择题(每小题4分,共12分)
1.在图(1)中,将方格纸中的图形绕O点顺时针旋转90°得到的图形是 ( )
2.如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F的位置,所转过的度数是 ( )
A.60° B.72° C.108° D.120°
3.如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是 ( )
A.72° B.108°
C.144° D.216°
二、填空题(每小题4分,共12分)
4.如图,图B是图A旋转后得到的,旋转中心是 ,旋转了 .
5.如图,直角△AOB顺时针旋转后与△COD重合,若∠AOD=127°,则旋转角度是
度.
6.如图,△ABC经过旋转得到△A′B′C′,且∠AOB=25°,∠AOB′=20°,则线段OB的对应线段是 ;∠OAB的对应角是 ;旋转中心是 ;旋转的角度是 .
三、解答题(共26分)
7.(8分)如图,P为等边三角形ABC内部一点,△ABP顺时针旋转后能与△CBP′重合.
(1)旋转中心是哪一点?旋转角是多少度?
(2)连结PP′,△BPP′是什么三角形?并说明你的理由.
8.(8分)在正方形ABCD中,点E在BC上,点F在AB上,
∠FDE=45°,△DEC按顺时针方向旋转一个角度后成
△DGA,如图所示.
(1)哪一个点是旋转中心,旋转角度等于多少?
(2)指出图中的对应线段和对应角.
(3)求∠GDF的度数.
【拓展延伸】
9.(10分)如图①,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;如图②,以BD为轴,把△ABD翻折180°,可以变到△CBD的位置;如图③,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
根据上面的说明,回答下列问题:
(1)在图④中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使△ABE变到△ADF的位置?
(2)指出图中线段BE与DF之间的关系,并说明理由.
答案解析
1.【解析】选B.将绕O点顺时针旋转90°得到的图形是.
2.【解析】选A.∵六边形ABCDEF是正六边形,
∴∠AFE=120°,
∴∠EFE′=180°-∠AFE=180°-120°=60°.
∵将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F的位置,
∴∠EFE′是旋转角,∴所转过的度数是60°.
3.【解析】选B.该图形被平分成五部分,旋转72°的整数倍,就可以与自身重合,因而A,C,D都正确,不能与其自身重合的是B.
4.【解析】确定图形的旋转时,首先要确定旋转前后的对应点,即可确定旋转中心,对应点连线的夹角即为旋转角;观察图形中Z点对应点的位置是图A绕旋转中心X旋转180°得到的.
答案:X 180°
5.【解析】对应点与旋转中心的连线的夹角,就是旋转角,∠BOD,∠AOC都是旋转角.由图可知,OB,OD是对应边,∠BOD是旋转角,所以,旋转角∠BOD=∠AOD-∠AOB
=127°-90°=37°.
答案:37
6.【解析】依题意,△ABC经过旋转得到△A′B′C′,
可知:旋转中心为点O,线段OB的对应线段为OB′,
∠OAB对应∠OA′B′,
旋转角∠BOB′=∠AOB+∠AOB′=25°+20°=45°.
答案:OB′ ∠OA′B′ 点O 45°
7.【解析】(1)根据题意,AB与BC重合,所以旋转中心是点B,旋转角等于∠ABC=
60°.
(2)△BPP′是等边三角形.∵旋转角为60°,即∠PBP′=60°,又BP=BP′,
∴△BPP′是等边三角形.
8.【解析】(1)D点是旋转中心,旋转角是90°.
(2)对应线段是DE和DG,DC和DA,CE和AG.
对应角是∠CDE和∠ADG,∠C和∠DAG,∠DEC和∠G.
(3)∵∠ADC=90°,∠FDE=45°,
∴∠ADF+∠EDC=45°,
∵∠GDA=∠EDC,∴∠ADF+∠GDA=45°,
即∠GDF=45°.
9.【解析】(1)将△ABE绕点A逆时针旋转90°而得到△ADF.
(2)BE与DF相等且互相垂直.
理由:根据旋转的性质,BE=DF;
延长BE交DF于点G,
∵∠ABG=∠ADF,∠AEB=∠DEG,
∴∠ADF+∠DEG=∠ABG+∠AEB=90°,
∴BG⊥DF.
一、选择题(每小题4分,共12分)
1.在图(1)中,将方格纸中的图形绕O点顺时针旋转90°得到的图形是 ( )
2.如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F的位置,所转过的度数是 ( )
A.60° B.72° C.108° D.120°
3.如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是 ( )
A.72° B.108°
C.144° D.216°
二、填空题(每小题4分,共12分)
4.如图,图B是图A旋转后得到的,旋转中心是 ,旋转了 .
5.如图,直角△AOB顺时针旋转后与△COD重合,若∠AOD=127°,则旋转角度是
度.
6.如图,△ABC经过旋转得到△A′B′C′,且∠AOB=25°,∠AOB′=20°,则线段OB的对应线段是 ;∠OAB的对应角是 ;旋转中心是 ;旋转的角度是 .
三、解答题(共26分)
7.(8分)如图,P为等边三角形ABC内部一点,△ABP顺时针旋转后能与△CBP′重合.
(1)旋转中心是哪一点?旋转角是多少度?
(2)连结PP′,△BPP′是什么三角形?并说明你的理由.
8.(8分)在正方形ABCD中,点E在BC上,点F在AB上,
∠FDE=45°,△DEC按顺时针方向旋转一个角度后成
△DGA,如图所示.
(1)哪一个点是旋转中心,旋转角度等于多少?
(2)指出图中的对应线段和对应角.
(3)求∠GDF的度数.
【拓展延伸】
9.(10分)如图①,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;如图②,以BD为轴,把△ABD翻折180°,可以变到△CBD的位置;如图③,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
根据上面的说明,回答下列问题:
(1)在图④中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使△ABE变到△ADF的位置?
(2)指出图中线段BE与DF之间的关系,并说明理由.
答案解析
1.【解析】选B.将绕O点顺时针旋转90°得到的图形是.
2.【解析】选A.∵六边形ABCDEF是正六边形,
∴∠AFE=120°,
∴∠EFE′=180°-∠AFE=180°-120°=60°.
∵将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F的位置,
∴∠EFE′是旋转角,∴所转过的度数是60°.
3.【解析】选B.该图形被平分成五部分,旋转72°的整数倍,就可以与自身重合,因而A,C,D都正确,不能与其自身重合的是B.
4.【解析】确定图形的旋转时,首先要确定旋转前后的对应点,即可确定旋转中心,对应点连线的夹角即为旋转角;观察图形中Z点对应点的位置是图A绕旋转中心X旋转180°得到的.
答案:X 180°
5.【解析】对应点与旋转中心的连线的夹角,就是旋转角,∠BOD,∠AOC都是旋转角.由图可知,OB,OD是对应边,∠BOD是旋转角,所以,旋转角∠BOD=∠AOD-∠AOB
=127°-90°=37°.
答案:37
6.【解析】依题意,△ABC经过旋转得到△A′B′C′,
可知:旋转中心为点O,线段OB的对应线段为OB′,
∠OAB对应∠OA′B′,
旋转角∠BOB′=∠AOB+∠AOB′=25°+20°=45°.
答案:OB′ ∠OA′B′ 点O 45°
7.【解析】(1)根据题意,AB与BC重合,所以旋转中心是点B,旋转角等于∠ABC=
60°.
(2)△BPP′是等边三角形.∵旋转角为60°,即∠PBP′=60°,又BP=BP′,
∴△BPP′是等边三角形.
8.【解析】(1)D点是旋转中心,旋转角是90°.
(2)对应线段是DE和DG,DC和DA,CE和AG.
对应角是∠CDE和∠ADG,∠C和∠DAG,∠DEC和∠G.
(3)∵∠ADC=90°,∠FDE=45°,
∴∠ADF+∠EDC=45°,
∵∠GDA=∠EDC,∴∠ADF+∠GDA=45°,
即∠GDF=45°.
9.【解析】(1)将△ABE绕点A逆时针旋转90°而得到△ADF.
(2)BE与DF相等且互相垂直.
理由:根据旋转的性质,BE=DF;
延长BE交DF于点G,
∵∠ABG=∠ADF,∠AEB=∠DEG,
∴∠ADF+∠DEG=∠ABG+∠AEB=90°,
∴BG⊥DF.
