10.5图形的全等课时作业(含解析)
文档属性
| 名称 | 10.5图形的全等课时作业(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-28 00:00:00 | ||
图片预览

文档简介
10.5图形的全等课时作业
一、选择题(每小题4分,共12分)
1.下列四组图形中,是全等图形的一组是 ( )
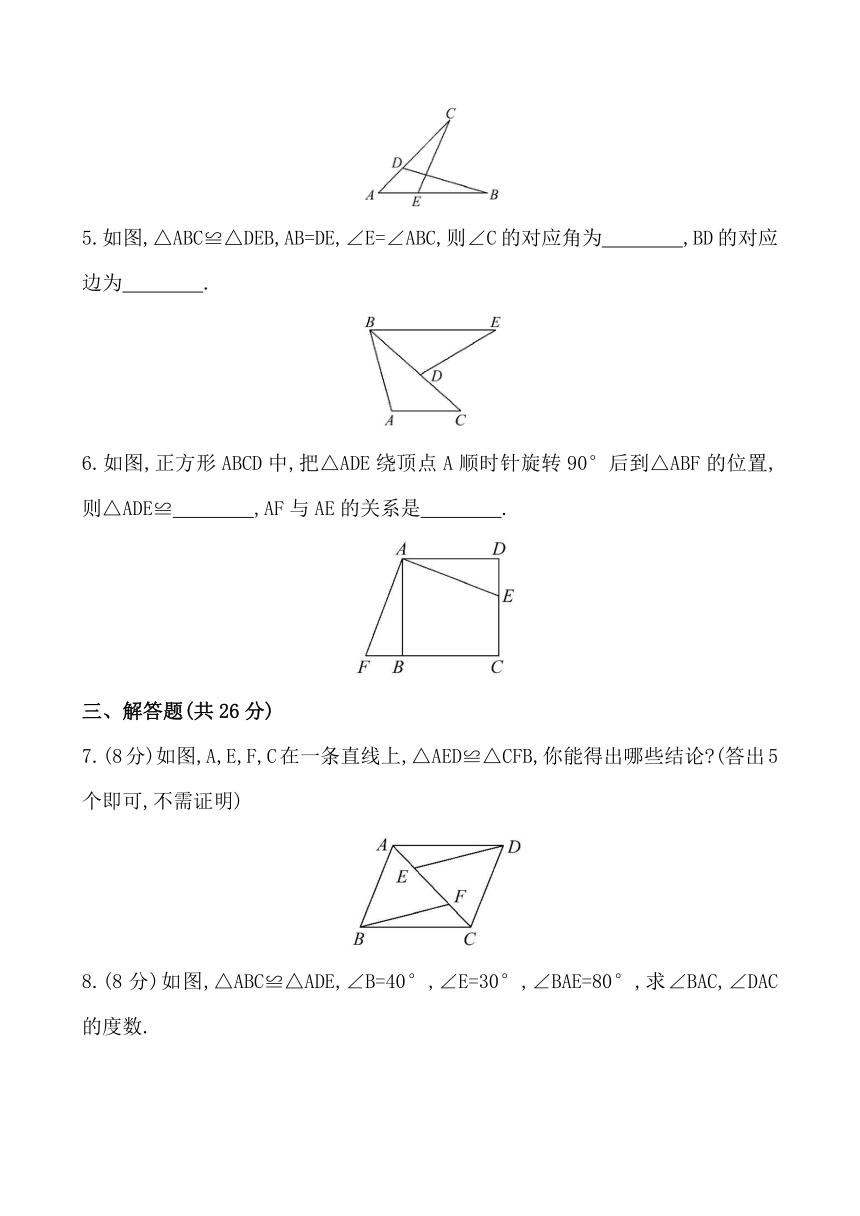
2.如图,已知CB=DB,△ABC≌△ABD,则∠C的对应角为 ( )
A.∠DAB B.∠D C.∠ABD D.∠CAD
3.如图,已知△ACE≌△DBF,下列结论中正确的个数是( )
①AC=DB;②AB=DC;
③∠1=∠2;④AE∥DF;
⑤S△ACE=S△DBF;⑥BC=AE;
⑦BF∥EC.
A.4个 B.5个 C.6个 D.7个
二、填空题(每小题4分,共12分)
4.如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8cm,BD=7cm,AD=3cm,则DC=
cm.
5.如图,△ABC≌△DEB,AB=DE,∠E=∠ABC,则∠C的对应角为 ,BD的对应边为 .
6.如图,正方形ABCD中,把△ADE绕顶点A顺时针旋转90°后到△ABF的位置,则△ADE≌ ,AF与AE的关系是 .
三、解答题(共26分)
7.(8分)如图,A,E,F,C在一条直线上,△AED≌△CFB,你能得出哪些结论?(答出5个即可,不需证明)
8.(8分)如图,△ABC≌△ADE,∠B=40°,∠E=30°,∠BAE=80°,求∠BAC,∠DAC的度数.
【拓展延伸】
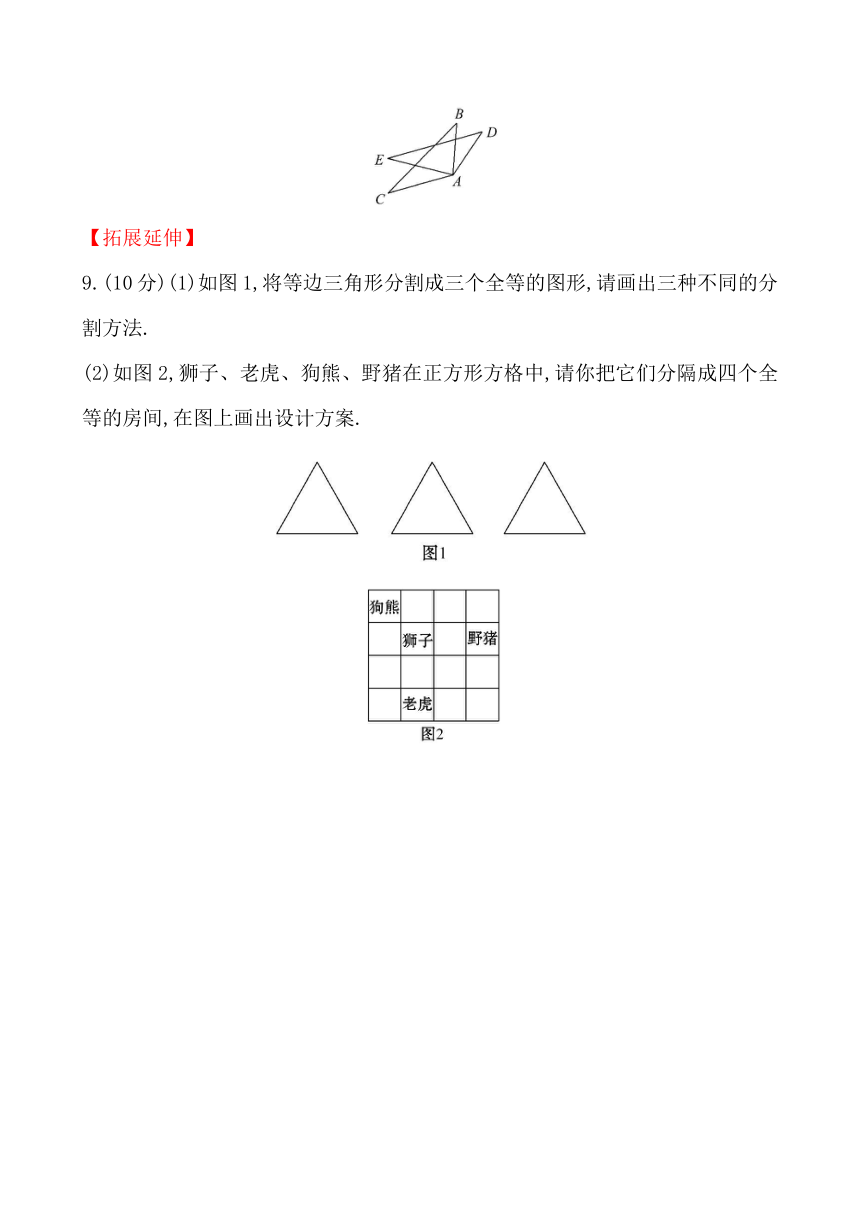
9.(10分)(1)如图1,将等边三角形分割成三个全等的图形,请画出三种不同的分割方法.
(2)如图2,狮子、老虎、狗熊、野猪在正方形方格中,请你把它们分隔成四个全等的房间,在图上画出设计方案.
答案解析
1.【解析】选C.由全等图形的概念可知:A,B项中的两个图形大小不等,D项中的形状不同,C项中的两个图形的大小和形状完全相同,符合全等图形的概念.
2.【解析】选B.根据全等图形的性质,全等三角形的对应角相等.
∵CB=DB,△ABC≌△ABD,∴∠C=∠D.
即∠C与∠D是对应角.
3.【解析】选C.∵△ACE≌△DBF,∴AC=DB,∠ECA=∠FBD,∠A=∠D,S△ACE=S△DBF.
∵AB+BC=CD+BC,∴AB=CD.
∵∠ECA=∠FBD,
∴BF∥EC,∠1=∠2.
∵∠A=∠D,∴AE∥DF.
又BC与AE不是对应边不一定相等,故6个正确.
4.【解析】∵△ABD≌△ACE,点B和点C是对应顶点,AB=8cm,AD=3cm,∴AC=AB=8cm,∴DC=AC-AD=5cm.
答案:5
5.【解析】要根据已知条件,并结合图形找准对应边、对应角,一般来说,大对大,小对小,中间对中间,本题中∠C与∠DBE都是处于中间大小的角,是对应角,BD与CA都是最短的边,是对应边.
答案:∠DBE CA
6.【解析】∵△ABF是△ADE绕顶点A顺时针旋转90°后得到的,
∴△ADE≌△ABF,∠EAF=90°,
∴AE与AF相等且互相垂直.
答案:△ABF AE与AF相等且互相垂直
7.【解析】根据全等图形的对应边相等,对应角相等即可解决.
△AED≌△CFB:AD=CB、AE=CF、ED=FB、∠ADE=∠CBF、∠AED=∠CFB、∠EAD=
∠FCB,
△ABF≌△CDE:AB=CD、AF=CE、∠ABF=∠CDE、∠BAF=∠DCE、∠AFB=∠CED,
△ABC≌△CDA:∠ABC=∠CDA.
(以上结论,答出5个即可).
8.【解析】∵△ABC≌△ADE,
∴∠B=∠D=40°,∠E=∠C=30°,
∴∠BAC=180°-∠B-∠C=110°.
∵∠BAE=80°,∠BAC=∠DAE=110°,
∴∠BAD=∠DAE-∠BAE=30°,
∴∠DAC=∠BAC+∠BAD=110°+30°=140°.
9.【解析】(1)方法一:连等边三角形的中心与各顶点.
方法二:连等边三角形的中心与各边中点.
方法三:连等边三角形的中心与各边上的一点,并且使AF=BD=CE.
(2)如图所示:
一、选择题(每小题4分,共12分)
1.下列四组图形中,是全等图形的一组是 ( )
2.如图,已知CB=DB,△ABC≌△ABD,则∠C的对应角为 ( )
A.∠DAB B.∠D C.∠ABD D.∠CAD
3.如图,已知△ACE≌△DBF,下列结论中正确的个数是( )
①AC=DB;②AB=DC;
③∠1=∠2;④AE∥DF;
⑤S△ACE=S△DBF;⑥BC=AE;
⑦BF∥EC.
A.4个 B.5个 C.6个 D.7个
二、填空题(每小题4分,共12分)
4.如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8cm,BD=7cm,AD=3cm,则DC=
cm.
5.如图,△ABC≌△DEB,AB=DE,∠E=∠ABC,则∠C的对应角为 ,BD的对应边为 .
6.如图,正方形ABCD中,把△ADE绕顶点A顺时针旋转90°后到△ABF的位置,则△ADE≌ ,AF与AE的关系是 .
三、解答题(共26分)
7.(8分)如图,A,E,F,C在一条直线上,△AED≌△CFB,你能得出哪些结论?(答出5个即可,不需证明)
8.(8分)如图,△ABC≌△ADE,∠B=40°,∠E=30°,∠BAE=80°,求∠BAC,∠DAC的度数.
【拓展延伸】
9.(10分)(1)如图1,将等边三角形分割成三个全等的图形,请画出三种不同的分割方法.
(2)如图2,狮子、老虎、狗熊、野猪在正方形方格中,请你把它们分隔成四个全等的房间,在图上画出设计方案.
答案解析
1.【解析】选C.由全等图形的概念可知:A,B项中的两个图形大小不等,D项中的形状不同,C项中的两个图形的大小和形状完全相同,符合全等图形的概念.
2.【解析】选B.根据全等图形的性质,全等三角形的对应角相等.
∵CB=DB,△ABC≌△ABD,∴∠C=∠D.
即∠C与∠D是对应角.
3.【解析】选C.∵△ACE≌△DBF,∴AC=DB,∠ECA=∠FBD,∠A=∠D,S△ACE=S△DBF.
∵AB+BC=CD+BC,∴AB=CD.
∵∠ECA=∠FBD,
∴BF∥EC,∠1=∠2.
∵∠A=∠D,∴AE∥DF.
又BC与AE不是对应边不一定相等,故6个正确.
4.【解析】∵△ABD≌△ACE,点B和点C是对应顶点,AB=8cm,AD=3cm,∴AC=AB=8cm,∴DC=AC-AD=5cm.
答案:5
5.【解析】要根据已知条件,并结合图形找准对应边、对应角,一般来说,大对大,小对小,中间对中间,本题中∠C与∠DBE都是处于中间大小的角,是对应角,BD与CA都是最短的边,是对应边.
答案:∠DBE CA
6.【解析】∵△ABF是△ADE绕顶点A顺时针旋转90°后得到的,
∴△ADE≌△ABF,∠EAF=90°,
∴AE与AF相等且互相垂直.
答案:△ABF AE与AF相等且互相垂直
7.【解析】根据全等图形的对应边相等,对应角相等即可解决.
△AED≌△CFB:AD=CB、AE=CF、ED=FB、∠ADE=∠CBF、∠AED=∠CFB、∠EAD=
∠FCB,
△ABF≌△CDE:AB=CD、AF=CE、∠ABF=∠CDE、∠BAF=∠DCE、∠AFB=∠CED,
△ABC≌△CDA:∠ABC=∠CDA.
(以上结论,答出5个即可).
8.【解析】∵△ABC≌△ADE,
∴∠B=∠D=40°,∠E=∠C=30°,
∴∠BAC=180°-∠B-∠C=110°.
∵∠BAE=80°,∠BAC=∠DAE=110°,
∴∠BAD=∠DAE-∠BAE=30°,
∴∠DAC=∠BAC+∠BAD=110°+30°=140°.
9.【解析】(1)方法一:连等边三角形的中心与各顶点.
方法二:连等边三角形的中心与各边中点.
方法三:连等边三角形的中心与各边上的一点,并且使AF=BD=CE.
(2)如图所示:
