人教版数学九年级上册 第二十三章 旋转 基础复习(含答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十三章 旋转 基础复习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 10:40:23 | ||
图片预览

文档简介
第二十三章基础复习
知识点1 图形的旋转
把一个平面图形绕平面内某一点转动一个角度,叫做图形的旋转.旋转三要素:旋转中心,旋转角,旋转方向.
旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
旋转作图步骤简单概括为:①连;②转;③截;④接;⑤写.
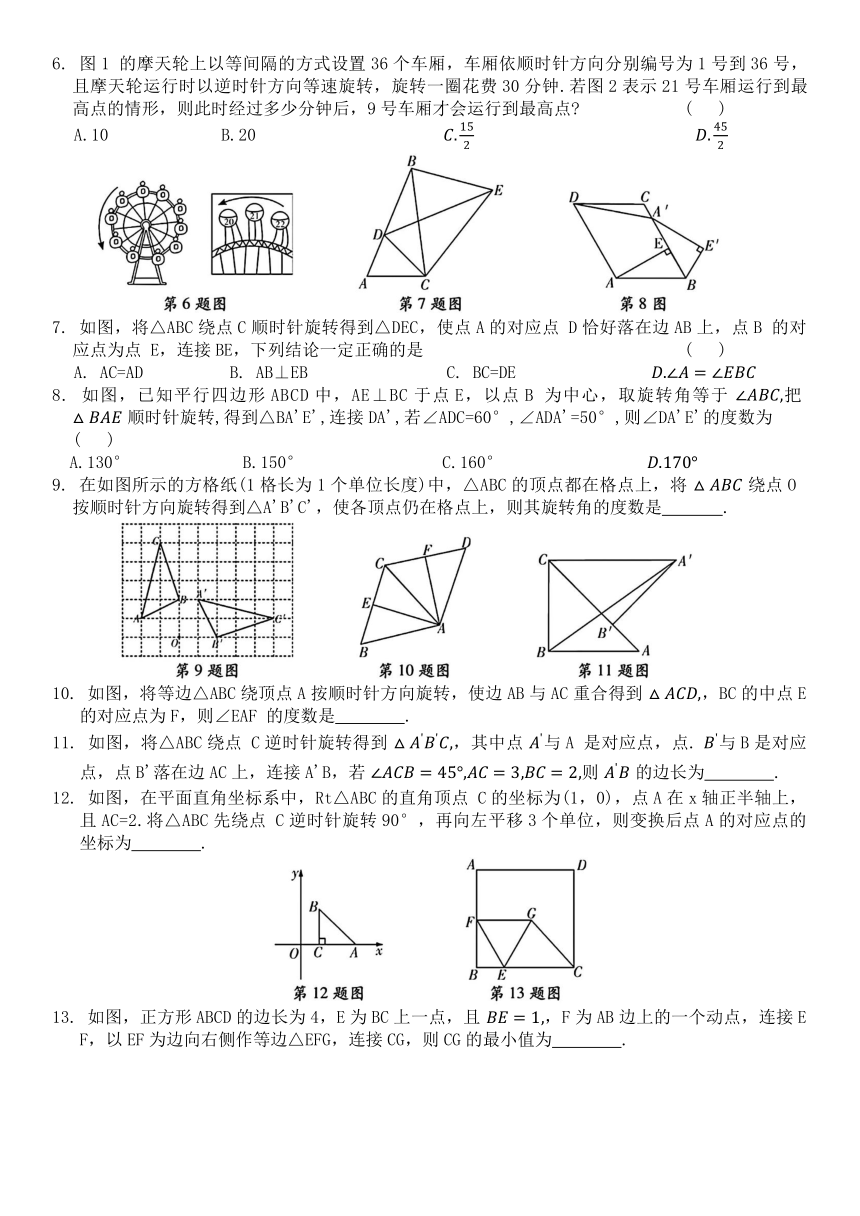
1. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为 ( )
A.30° B.90° C.120° D.180°
2. 如图,将△OAB绕点O逆时针旋转70°,到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45° B.40° C.35° D.30°
3. 如图,将线段AB先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段. 则点 B 的对应点 B'的坐标是 ( )
B.(-1,2) C.(4,-1) D.(1,-2)
4. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC 绕点 A 顺时针旋转得到 ,当点 B的对应点 D 恰好落在 BC边上时,CD 的长为 ( )
A.1.6 B.1.8 C.2 D.2.6
5. 如图,正方形 OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把 旋转 ,则旋转后点 D 的对应点 D'的坐标是 ( )
A.(2,10) B.(2,10)或(-2,0) C.(-2,0) D.(10,2)或(-2,0)
6. 图1 的摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,9号车厢才会运行到最高点 ( )
A.10 B.20
7. 如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点 D恰好落在边AB上,点B 的对应点为点 E,连接BE,下列结论一定正确的是 ( )
A. AC=AD B. AB⊥EB C. BC=DE
8. 如图,已知平行四边形ABCD中,AE⊥BC于点E,以点B 为中心,取旋转角等于 把 顺时针旋转,得到△BA'E',连接DA',若∠ADC=60°,∠ADA'=50°,则∠DA'E'的度数为 ( )
A.130° B.150° C.160°
9. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将 绕点O 按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .
10. 如图,将等边△ABC绕顶点A按顺时针方向旋转,使边AB与AC重合得到 ,BC的中点E的对应点为F,则∠EAF 的度数是 .
11. 如图,将△ABC绕点 C逆时针旋转得到 ,其中点 与A 是对应点,点. 与B是对应点,点B'落在边AC上,连接A'B,若 则 的边长为 .
12. 如图,在平面直角坐标系中,Rt△ABC的直角顶点 C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点 C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为 .
13. 如图,正方形ABCD的边长为4,E为BC上一点,且 ,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
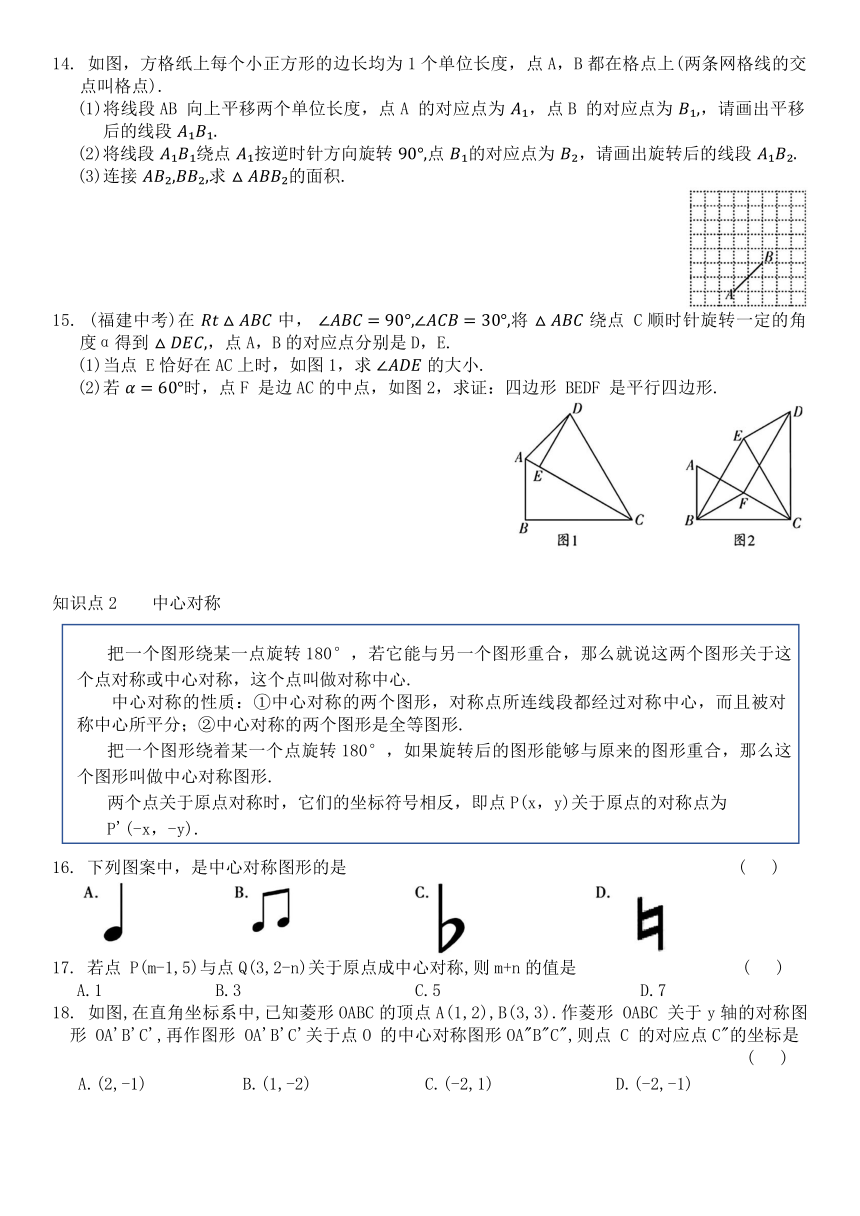
14. 如图,方格纸上每个小正方形的边长均为1个单位长度,点A,B都在格点上(两条网格线的交点叫格点).
(1)将线段AB 向上平移两个单位长度,点A 的对应点为 ,点B 的对应点为 ,请画出平移后的线段
(2)将线段 绕点 按逆时针方向旋转 点 的对应点为 ,请画出旋转后的线段
(3)连接 求 的面积.
15. (福建中考)在 中, 将 绕点 C顺时针旋转一定的角度α得到 ,点A,B的对应点分别是D,E.
(1)当点 E恰好在AC上时,如图1,求 的大小.
(2)若 时,点F 是边AC的中点,如图2,求证:四边形 BEDF 是平行四边形.
知识点2 中心对称
把一个图形绕某一点旋转180°,若它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.
中心对称的性质:①中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;②中心对称的两个图形是全等图形.
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为
P'(-x,-y).
16. 下列图案中,是中心对称图形的是 ( )
17. 若点 P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是 ( )
A.1 B.3 C.5 D.7
18. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形 OABC 关于y轴的对称图形 OA'B'C',再作图形 OA'B'C'关于点O 的中心对称图形OA"B"C",则点 C 的对应点C"的坐标是 ( )
A.(2,-1) B.(1,-2) C.(-2,1) D.(-2,-1)
19. 4张扑克牌如图1所示放在桌子上,华华把其中一张旋转180°后得到如图2 所示,那么他所旋转的牌从左起是 ( )
A.第一张或第二张 B. 第三张或第四张 C.第二张或第三张 D.第一张或第四张
20. 如果点A(3-m,2)在函数y=2x-3的图象上,则点A关于原点对称的点的坐标是 .
21. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 种.
22. 已知:在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点成中心对称的△A B C .
(2)画出将A B C 绕点 C 顺时针旋转90°所得的△A B C .
知识点3 课题学习 图案设计
图形之间的基本变换有轴对称、平移、旋转三种基本形式,但较多的形式都是经过组合变化而成的.
在设计图案中,可以利用轴对称、平移和旋转或它们的组合进行图案设计.
23. 下面的四个图案中,既可以用旋转来分析整个图案的形成过程,又可以用轴对称来分析整个图案的形成过程的图案有 ( )
A.4个 B.3个 C.2个 D.1个
24. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
(1)使得6个阴影小等边三角形组成一个轴对称图形.
(2)使得6个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
第二十三章基础复习
1. C 2. D 3. D 4. A 5. B 6. B 7. D 8. C 9.90°
14.解:(1)线段. 如图所示.
(2)线段 如图所示.
15.(1)解: 绕点 C顺时针旋转α得到. 点 E 恰好在AC上,
,
(2)证明:如图,连接AE.∵ 点 F是边AC中点,
∴BF=AB,
∵ △ABC 绕点 C 顺时针旋转 60°得到△DEC,
∴ ∠BCE = ∠ACD =60°,CB = CE,DE=AB,
∴DE=BF,△ACD和△BCE为等边三角形,∴BE=CB,
∵点 F为△ACD的边AC的中点,
∴DF⊥AC,易证得△CFD≌△ABC,∴DF=BC,
∴DF=BE,而BF=DE,∴四边形 BEDF 是平行四边形.
16. D17. C 18. A 19. A
22.解:(1)如图所示, 即为所求.
(2)如图所示, 即为所求.
23. A
24.解:(1)如图1所示,6个阴影小等边三角形组成一个轴对称图形.(答案不唯一)
(2)如图2所示,6个阴影小等边三角形组成一个中心对称图形.(答案不唯一)
知识点1 图形的旋转
把一个平面图形绕平面内某一点转动一个角度,叫做图形的旋转.旋转三要素:旋转中心,旋转角,旋转方向.
旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
旋转作图步骤简单概括为:①连;②转;③截;④接;⑤写.
1. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为 ( )
A.30° B.90° C.120° D.180°
2. 如图,将△OAB绕点O逆时针旋转70°,到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45° B.40° C.35° D.30°
3. 如图,将线段AB先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段. 则点 B 的对应点 B'的坐标是 ( )
B.(-1,2) C.(4,-1) D.(1,-2)
4. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC 绕点 A 顺时针旋转得到 ,当点 B的对应点 D 恰好落在 BC边上时,CD 的长为 ( )
A.1.6 B.1.8 C.2 D.2.6
5. 如图,正方形 OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把 旋转 ,则旋转后点 D 的对应点 D'的坐标是 ( )
A.(2,10) B.(2,10)或(-2,0) C.(-2,0) D.(10,2)或(-2,0)
6. 图1 的摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,9号车厢才会运行到最高点 ( )
A.10 B.20
7. 如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点 D恰好落在边AB上,点B 的对应点为点 E,连接BE,下列结论一定正确的是 ( )
A. AC=AD B. AB⊥EB C. BC=DE
8. 如图,已知平行四边形ABCD中,AE⊥BC于点E,以点B 为中心,取旋转角等于 把 顺时针旋转,得到△BA'E',连接DA',若∠ADC=60°,∠ADA'=50°,则∠DA'E'的度数为 ( )
A.130° B.150° C.160°
9. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将 绕点O 按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .
10. 如图,将等边△ABC绕顶点A按顺时针方向旋转,使边AB与AC重合得到 ,BC的中点E的对应点为F,则∠EAF 的度数是 .
11. 如图,将△ABC绕点 C逆时针旋转得到 ,其中点 与A 是对应点,点. 与B是对应点,点B'落在边AC上,连接A'B,若 则 的边长为 .
12. 如图,在平面直角坐标系中,Rt△ABC的直角顶点 C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点 C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为 .
13. 如图,正方形ABCD的边长为4,E为BC上一点,且 ,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
14. 如图,方格纸上每个小正方形的边长均为1个单位长度,点A,B都在格点上(两条网格线的交点叫格点).
(1)将线段AB 向上平移两个单位长度,点A 的对应点为 ,点B 的对应点为 ,请画出平移后的线段
(2)将线段 绕点 按逆时针方向旋转 点 的对应点为 ,请画出旋转后的线段
(3)连接 求 的面积.
15. (福建中考)在 中, 将 绕点 C顺时针旋转一定的角度α得到 ,点A,B的对应点分别是D,E.
(1)当点 E恰好在AC上时,如图1,求 的大小.
(2)若 时,点F 是边AC的中点,如图2,求证:四边形 BEDF 是平行四边形.
知识点2 中心对称
把一个图形绕某一点旋转180°,若它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.
中心对称的性质:①中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;②中心对称的两个图形是全等图形.
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为
P'(-x,-y).
16. 下列图案中,是中心对称图形的是 ( )
17. 若点 P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是 ( )
A.1 B.3 C.5 D.7
18. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形 OABC 关于y轴的对称图形 OA'B'C',再作图形 OA'B'C'关于点O 的中心对称图形OA"B"C",则点 C 的对应点C"的坐标是 ( )
A.(2,-1) B.(1,-2) C.(-2,1) D.(-2,-1)
19. 4张扑克牌如图1所示放在桌子上,华华把其中一张旋转180°后得到如图2 所示,那么他所旋转的牌从左起是 ( )
A.第一张或第二张 B. 第三张或第四张 C.第二张或第三张 D.第一张或第四张
20. 如果点A(3-m,2)在函数y=2x-3的图象上,则点A关于原点对称的点的坐标是 .
21. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 种.
22. 已知:在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点成中心对称的△A B C .
(2)画出将A B C 绕点 C 顺时针旋转90°所得的△A B C .
知识点3 课题学习 图案设计
图形之间的基本变换有轴对称、平移、旋转三种基本形式,但较多的形式都是经过组合变化而成的.
在设计图案中,可以利用轴对称、平移和旋转或它们的组合进行图案设计.
23. 下面的四个图案中,既可以用旋转来分析整个图案的形成过程,又可以用轴对称来分析整个图案的形成过程的图案有 ( )
A.4个 B.3个 C.2个 D.1个
24. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
(1)使得6个阴影小等边三角形组成一个轴对称图形.
(2)使得6个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
第二十三章基础复习
1. C 2. D 3. D 4. A 5. B 6. B 7. D 8. C 9.90°
14.解:(1)线段. 如图所示.
(2)线段 如图所示.
15.(1)解: 绕点 C顺时针旋转α得到. 点 E 恰好在AC上,
,
(2)证明:如图,连接AE.∵ 点 F是边AC中点,
∴BF=AB,
∵ △ABC 绕点 C 顺时针旋转 60°得到△DEC,
∴ ∠BCE = ∠ACD =60°,CB = CE,DE=AB,
∴DE=BF,△ACD和△BCE为等边三角形,∴BE=CB,
∵点 F为△ACD的边AC的中点,
∴DF⊥AC,易证得△CFD≌△ABC,∴DF=BC,
∴DF=BE,而BF=DE,∴四边形 BEDF 是平行四边形.
16. D17. C 18. A 19. A
22.解:(1)如图所示, 即为所求.
(2)如图所示, 即为所求.
23. A
24.解:(1)如图1所示,6个阴影小等边三角形组成一个轴对称图形.(答案不唯一)
(2)如图2所示,6个阴影小等边三角形组成一个中心对称图形.(答案不唯一)
同课章节目录
