人教版数学九年级上册 第二十三章 旋转综合 测试卷(含答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十三章 旋转综合 测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
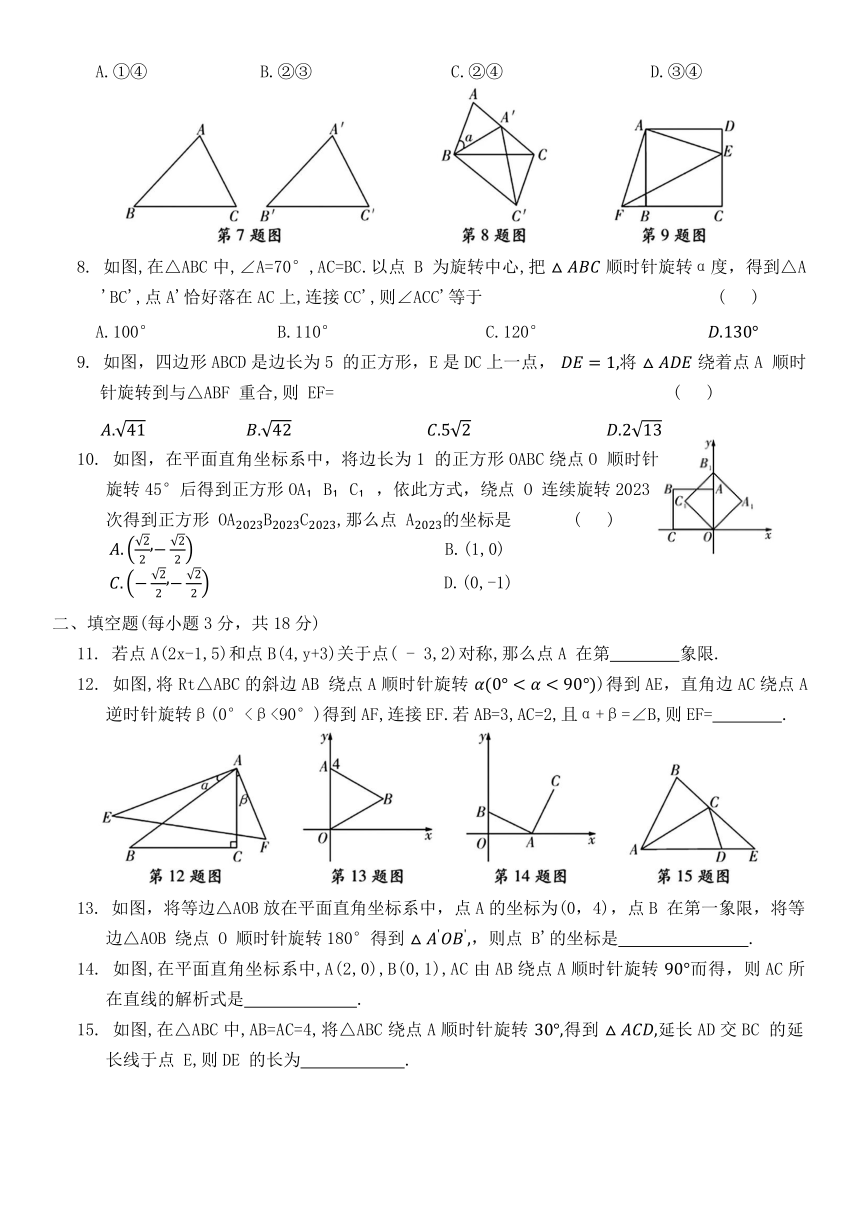
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 10:40:59 | ||
图片预览

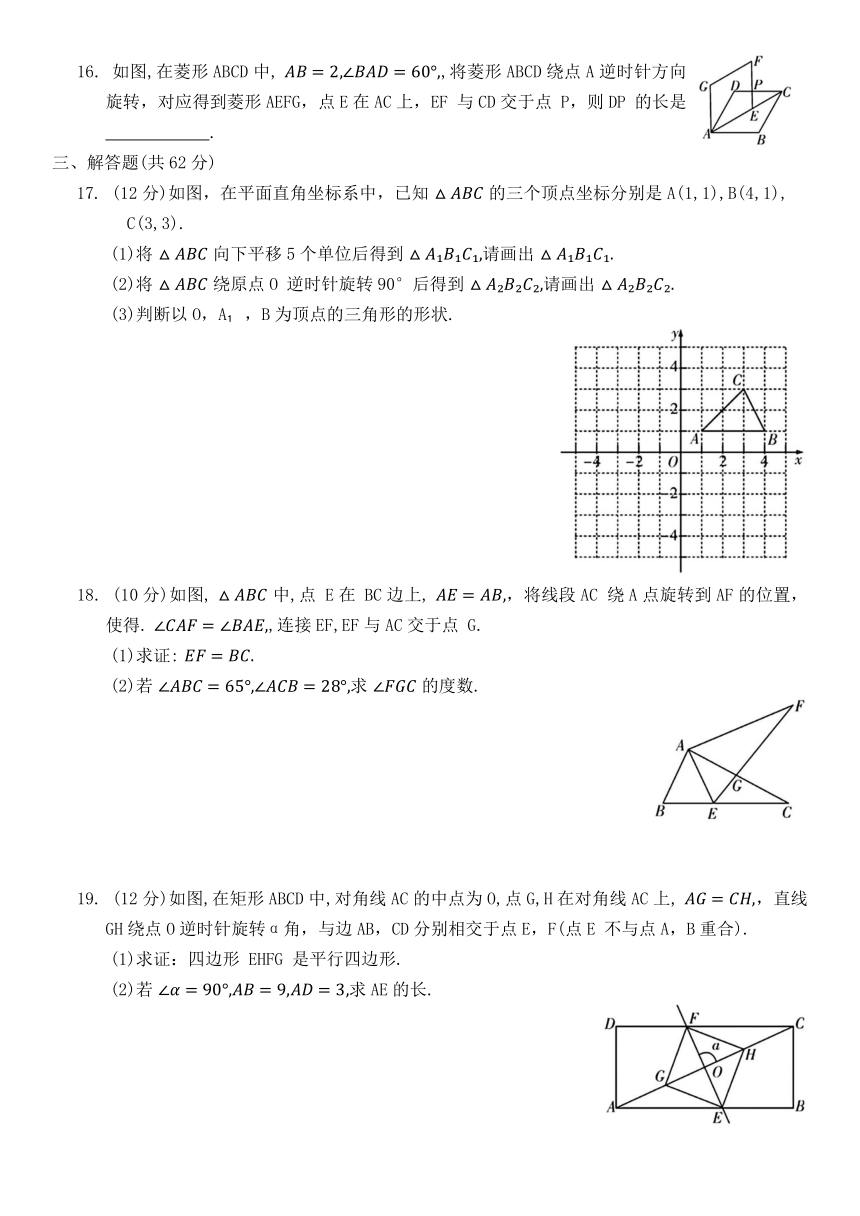
文档简介
第二十三章综合测试卷
时间:120 分钟 满分:120 分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 下列图形中,属于中心对称图形的是 ( )
2. 已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是 ( )
3. 在平面直角坐标系中,点A的坐标为(1, ),以原点为中心,将点A顺时针旋转30°得到点 A',则点 A'的坐标为 ( )
C.(2,1) D.(0,2)
4. 如图, ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点A的坐标为(-2,3),则点 C 的坐标为 ( )
A.(-3,2) B.(-2,-3) C.(3,-2) D.(2,-3)
5. 如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB',使点 B 的对应点B'落在x轴的正半轴上,则点 B'的坐标是 ( )
A.(5,0) B.(8,0) C.(0,5) D.(0,8)
6. 如图,点E 是正方形ABCD的边 DC上一点,把△ADE 绕点A 顺时针旋转90°到△ABF的位置.若四边形AECF 的面积为20,DE=2,则AE的长为 ( )
A.4 C.6
7. 如图,△A'B'C'是由△ABC经过平移得到的, 还可以看作是 经过怎样的图形变化得到 下列结论:①1次旋转;②1 次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是 ( )
A.①④ B.②③ C.②④ D.③④
8. 如图,在△ABC中,∠A=70°,AC=BC.以点 B 为旋转中心,把 顺时针旋转α度,得到△A'BC',点A'恰好落在AC上,连接CC',则∠ACC'等于 ( )
A.100° B.110° C.120°
9. 如图,四边形ABCD是边长为5 的正方形,E是DC上一点, 将 绕着点A 顺时针旋转到与△ABF 重合,则 EF= ( )
10. 如图,在平面直角坐标系中,将边长为1 的正方形OABC绕点O 顺时针旋转45°后得到正方形OA B C ,依此方式,绕点 O 连续旋转2023 次得到正方形 ,那么点 的坐标是 ( )
B.(1,0)
D.(0,-1)
二、填空题(每小题3分,共18分)
11. 若点A(2x-1,5)和点B(4,y+3)关于点( - 3,2)对称,那么点A 在第 象限.
12. 如图,将Rt△ABC的斜边AB 绕点A顺时针旋转 )得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF.若AB=3,AC=2,且α+β=∠B,则EF= .
13. 如图,将等边△AOB放在平面直角坐标系中,点A的坐标为(0,4),点B 在第一象限,将等边△AOB 绕点 O 顺时针旋转180°得到 ,则点 B'的坐标是 .
14. 如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转 而得,则AC所在直线的解析式是 .
15. 如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转 得到 延长AD交BC 的延长线于点 E,则DE 的长为 .
16. 如图,在菱形ABCD中, ,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF 与CD交于点 P,则DP 的长是 .
三、解答题(共62分)
17. (12分)如图,在平面直角坐标系中,已知 的三个顶点坐标分别是A(1,1),B(4,1), C(3,3).
(1)将 向下平移5个单位后得到 请画出
(2)将 绕原点O 逆时针旋转90°后得到 请画出
(3)判断以O,A ,B为顶点的三角形的形状.
18. (10分)如图, 中,点 E在 BC边上, ,将线段AC 绕A点旋转到AF的位置,使得. ,连接EF,EF与AC交于点 G.
(1)求证:
(2)若 求 的度数.
19. (12分)如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上, ,直线GH绕点O逆时针旋转α角,与边AB,CD分别相交于点E,F(点E 不与点A,B重合).
(1)求证:四边形 EHFG 是平行四边形.
(2)若 求AE的长.
20. (14分)如图1,点O 为直线AB上一点,过点O 作射线OC,使 ,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O 按逆时针方向旋转至图2的位置,使得ON落在射线OB 上,此时三角板旋转的角度为 度.
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3 的位置,使得ON在. 的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由.
(3)在上述直角三角板从图1 逆时针旋转到图3 的位置的过程中,若三角板绕点O按 每秒的速度旋转,当直角三角板的直角边 ON所在直线恰好平分 时,求此时三角板绕点O 的运动时间t的值.
21. (14分)如图1,在 中, ,将 绕点 C 旋转,边AB 分别交边CN,CM于D,E两点.
(1)若 ,求CD 的最小值.
(2)如图2,设 ,点G是AB的中点,连接CG,当. 旋转到 CN与AB 的交点 D 是BG的中点时,过点 D 作CD的垂线交 CM 于点 F,连接GF,AF,求证:
第二十三章综合测试卷
C 2. C 3. A 4. D 5. B 6. D7. D 8. B 9. D 10. A11.二 12.
14. y=2x-4
16. -1
17.解:(1)如图所示, 即为所求.
(2)如图所示, 即为所求.
为等腰直角三角形.
18.(1)证明:∵ ∠CAF =∠BAE,∴∠BAC =∠EAF.∵ 将线段AC绕A点旋转到AF的位置,∴AC=AF.在△ABC 与△AEF
中,
(2)解:∵AB=AE,∠ABC=65°,∴∠BAE=180°-65°×2=50°,∴ ∠FAG =∠BAE =50°.
∵ △ABC≌△AEF,∴ ∠F=∠C=28°,∴∠FGC=∠FAG+∠F=50°+28°=78°.
19.(1)证明:∵对角线AC的中点为O,∴AO=CO,又AG=CH,∴GO=HO.∵ 四边形 ABCD 是矩形,∴AD =BC,CD =AB,CD∥AB,∴ ∠DCA =∠CAB,又 CO =AO,∠FOC =∠EOA,∴△COF≌△AOE(ASA),∴FO=EO,∴四边形 EHFG 是平行四边形.
(2)解:如图,连接CE,又α=90°,∴EF⊥AC,且AO=CO,∴EF是AC的垂直平分线,AE=CE,在 Rt△BCE 中,
即 解得AE=5.
20.解:(1)由旋转的性质知,旋转角∠MON =90°.故答案为:90.
(2)∠AOM-∠NOC=30°.理由如下:设∠AOC=α,由∠AOC:∠BOC=1:2,得∠BOC=2α.
∵∠AOC+∠BOC=180°,∴α+2α=180°,解得α=60°,即∠AOC=60°.
∴ ∠AON +∠NOC=60°①.∵ ∠MON =90°,
∴ ∠AOM + ∠AON =90°②.由②-①,得∠AOM--∠NOC=30°.
(3)如图4,当直角边 ON 在∠AOC 外部时,由 ON 平分∠AOC,得∠BON =30°.因此三角板绕点 O 逆时针旋转60°,此时三角板的运动时间为:t=60°÷15°=4(秒).
如图5,当直角边ON在∠AOC 内部时,由 ON平分∠AOC,可得∠CON=30°.因此三角板绕点 O 逆时针旋转240°,此时三角板的运动时间为:t=240°÷15°=16(秒).
综上所述,三角板绕点O的运动时间t为4秒或16秒.
21.(1)解:当CD⊥AB时,CD的值最小,
∵∠BCA=90°,AC=8,
∴CD 的最小值
(2)证明:如图,延长 FD 至点 K,使得DK=FD,连接CK,BK.
∵点D是BG的中点,∴DG=BD,
∵∠GDF=∠BDK,
∴△GDF≌△BDK(SAS).
∴FG=BK,∠FGD=∠KBD,
∵CD⊥ FD,∠MCN=45°,DK=FD,
∴CF=CK,∠DCK=45°,
∵∠MCN=45°,∠BCA=90°,
∴∠ACF+∠BCD=45°,∵∠DCK=∠BCK+∠BCD,
∴∠ACF=∠BCK.∵AC=BC,∴ △ACF≌△BCK(SAS).
∴AF=BK,∠CAF=∠CBK,∴AF=GF,∴∠GAF=∠AGF.
∵∠BCA=90°,AC=BC,∴∠CAB=∠CBA=45°.
∵∠CBA+∠CBK=∠DBK=∠FGD=180°-∠AGF,∠CBK
=∠CAF=∠CAB+∠FAG.∴∠FAG=∠AGF=45°.
∴AG= FG,∵∠BCA=90°,AC=BC,点G是AB的中点,∴CG=AG,∴CG= FG.
时间:120 分钟 满分:120 分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 下列图形中,属于中心对称图形的是 ( )
2. 已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是 ( )
3. 在平面直角坐标系中,点A的坐标为(1, ),以原点为中心,将点A顺时针旋转30°得到点 A',则点 A'的坐标为 ( )
C.(2,1) D.(0,2)
4. 如图, ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点A的坐标为(-2,3),则点 C 的坐标为 ( )
A.(-3,2) B.(-2,-3) C.(3,-2) D.(2,-3)
5. 如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB',使点 B 的对应点B'落在x轴的正半轴上,则点 B'的坐标是 ( )
A.(5,0) B.(8,0) C.(0,5) D.(0,8)
6. 如图,点E 是正方形ABCD的边 DC上一点,把△ADE 绕点A 顺时针旋转90°到△ABF的位置.若四边形AECF 的面积为20,DE=2,则AE的长为 ( )
A.4 C.6
7. 如图,△A'B'C'是由△ABC经过平移得到的, 还可以看作是 经过怎样的图形变化得到 下列结论:①1次旋转;②1 次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是 ( )
A.①④ B.②③ C.②④ D.③④
8. 如图,在△ABC中,∠A=70°,AC=BC.以点 B 为旋转中心,把 顺时针旋转α度,得到△A'BC',点A'恰好落在AC上,连接CC',则∠ACC'等于 ( )
A.100° B.110° C.120°
9. 如图,四边形ABCD是边长为5 的正方形,E是DC上一点, 将 绕着点A 顺时针旋转到与△ABF 重合,则 EF= ( )
10. 如图,在平面直角坐标系中,将边长为1 的正方形OABC绕点O 顺时针旋转45°后得到正方形OA B C ,依此方式,绕点 O 连续旋转2023 次得到正方形 ,那么点 的坐标是 ( )
B.(1,0)
D.(0,-1)
二、填空题(每小题3分,共18分)
11. 若点A(2x-1,5)和点B(4,y+3)关于点( - 3,2)对称,那么点A 在第 象限.
12. 如图,将Rt△ABC的斜边AB 绕点A顺时针旋转 )得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF.若AB=3,AC=2,且α+β=∠B,则EF= .
13. 如图,将等边△AOB放在平面直角坐标系中,点A的坐标为(0,4),点B 在第一象限,将等边△AOB 绕点 O 顺时针旋转180°得到 ,则点 B'的坐标是 .
14. 如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转 而得,则AC所在直线的解析式是 .
15. 如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转 得到 延长AD交BC 的延长线于点 E,则DE 的长为 .
16. 如图,在菱形ABCD中, ,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF 与CD交于点 P,则DP 的长是 .
三、解答题(共62分)
17. (12分)如图,在平面直角坐标系中,已知 的三个顶点坐标分别是A(1,1),B(4,1), C(3,3).
(1)将 向下平移5个单位后得到 请画出
(2)将 绕原点O 逆时针旋转90°后得到 请画出
(3)判断以O,A ,B为顶点的三角形的形状.
18. (10分)如图, 中,点 E在 BC边上, ,将线段AC 绕A点旋转到AF的位置,使得. ,连接EF,EF与AC交于点 G.
(1)求证:
(2)若 求 的度数.
19. (12分)如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上, ,直线GH绕点O逆时针旋转α角,与边AB,CD分别相交于点E,F(点E 不与点A,B重合).
(1)求证:四边形 EHFG 是平行四边形.
(2)若 求AE的长.
20. (14分)如图1,点O 为直线AB上一点,过点O 作射线OC,使 ,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O 按逆时针方向旋转至图2的位置,使得ON落在射线OB 上,此时三角板旋转的角度为 度.
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3 的位置,使得ON在. 的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由.
(3)在上述直角三角板从图1 逆时针旋转到图3 的位置的过程中,若三角板绕点O按 每秒的速度旋转,当直角三角板的直角边 ON所在直线恰好平分 时,求此时三角板绕点O 的运动时间t的值.
21. (14分)如图1,在 中, ,将 绕点 C 旋转,边AB 分别交边CN,CM于D,E两点.
(1)若 ,求CD 的最小值.
(2)如图2,设 ,点G是AB的中点,连接CG,当. 旋转到 CN与AB 的交点 D 是BG的中点时,过点 D 作CD的垂线交 CM 于点 F,连接GF,AF,求证:
第二十三章综合测试卷
C 2. C 3. A 4. D 5. B 6. D7. D 8. B 9. D 10. A11.二 12.
14. y=2x-4
16. -1
17.解:(1)如图所示, 即为所求.
(2)如图所示, 即为所求.
为等腰直角三角形.
18.(1)证明:∵ ∠CAF =∠BAE,∴∠BAC =∠EAF.∵ 将线段AC绕A点旋转到AF的位置,∴AC=AF.在△ABC 与△AEF
中,
(2)解:∵AB=AE,∠ABC=65°,∴∠BAE=180°-65°×2=50°,∴ ∠FAG =∠BAE =50°.
∵ △ABC≌△AEF,∴ ∠F=∠C=28°,∴∠FGC=∠FAG+∠F=50°+28°=78°.
19.(1)证明:∵对角线AC的中点为O,∴AO=CO,又AG=CH,∴GO=HO.∵ 四边形 ABCD 是矩形,∴AD =BC,CD =AB,CD∥AB,∴ ∠DCA =∠CAB,又 CO =AO,∠FOC =∠EOA,∴△COF≌△AOE(ASA),∴FO=EO,∴四边形 EHFG 是平行四边形.
(2)解:如图,连接CE,又α=90°,∴EF⊥AC,且AO=CO,∴EF是AC的垂直平分线,AE=CE,在 Rt△BCE 中,
即 解得AE=5.
20.解:(1)由旋转的性质知,旋转角∠MON =90°.故答案为:90.
(2)∠AOM-∠NOC=30°.理由如下:设∠AOC=α,由∠AOC:∠BOC=1:2,得∠BOC=2α.
∵∠AOC+∠BOC=180°,∴α+2α=180°,解得α=60°,即∠AOC=60°.
∴ ∠AON +∠NOC=60°①.∵ ∠MON =90°,
∴ ∠AOM + ∠AON =90°②.由②-①,得∠AOM--∠NOC=30°.
(3)如图4,当直角边 ON 在∠AOC 外部时,由 ON 平分∠AOC,得∠BON =30°.因此三角板绕点 O 逆时针旋转60°,此时三角板的运动时间为:t=60°÷15°=4(秒).
如图5,当直角边ON在∠AOC 内部时,由 ON平分∠AOC,可得∠CON=30°.因此三角板绕点 O 逆时针旋转240°,此时三角板的运动时间为:t=240°÷15°=16(秒).
综上所述,三角板绕点O的运动时间t为4秒或16秒.
21.(1)解:当CD⊥AB时,CD的值最小,
∵∠BCA=90°,AC=8,
∴CD 的最小值
(2)证明:如图,延长 FD 至点 K,使得DK=FD,连接CK,BK.
∵点D是BG的中点,∴DG=BD,
∵∠GDF=∠BDK,
∴△GDF≌△BDK(SAS).
∴FG=BK,∠FGD=∠KBD,
∵CD⊥ FD,∠MCN=45°,DK=FD,
∴CF=CK,∠DCK=45°,
∵∠MCN=45°,∠BCA=90°,
∴∠ACF+∠BCD=45°,∵∠DCK=∠BCK+∠BCD,
∴∠ACF=∠BCK.∵AC=BC,∴ △ACF≌△BCK(SAS).
∴AF=BK,∠CAF=∠CBK,∴AF=GF,∴∠GAF=∠AGF.
∵∠BCA=90°,AC=BC,∴∠CAB=∠CBA=45°.
∵∠CBA+∠CBK=∠DBK=∠FGD=180°-∠AGF,∠CBK
=∠CAF=∠CAB+∠FAG.∴∠FAG=∠AGF=45°.
∴AG= FG,∵∠BCA=90°,AC=BC,点G是AB的中点,∴CG=AG,∴CG= FG.
同课章节目录
