人教版数学九年级上册 期中 综合测试卷(含答案)
文档属性
| 名称 | 人教版数学九年级上册 期中 综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 990.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
期中综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
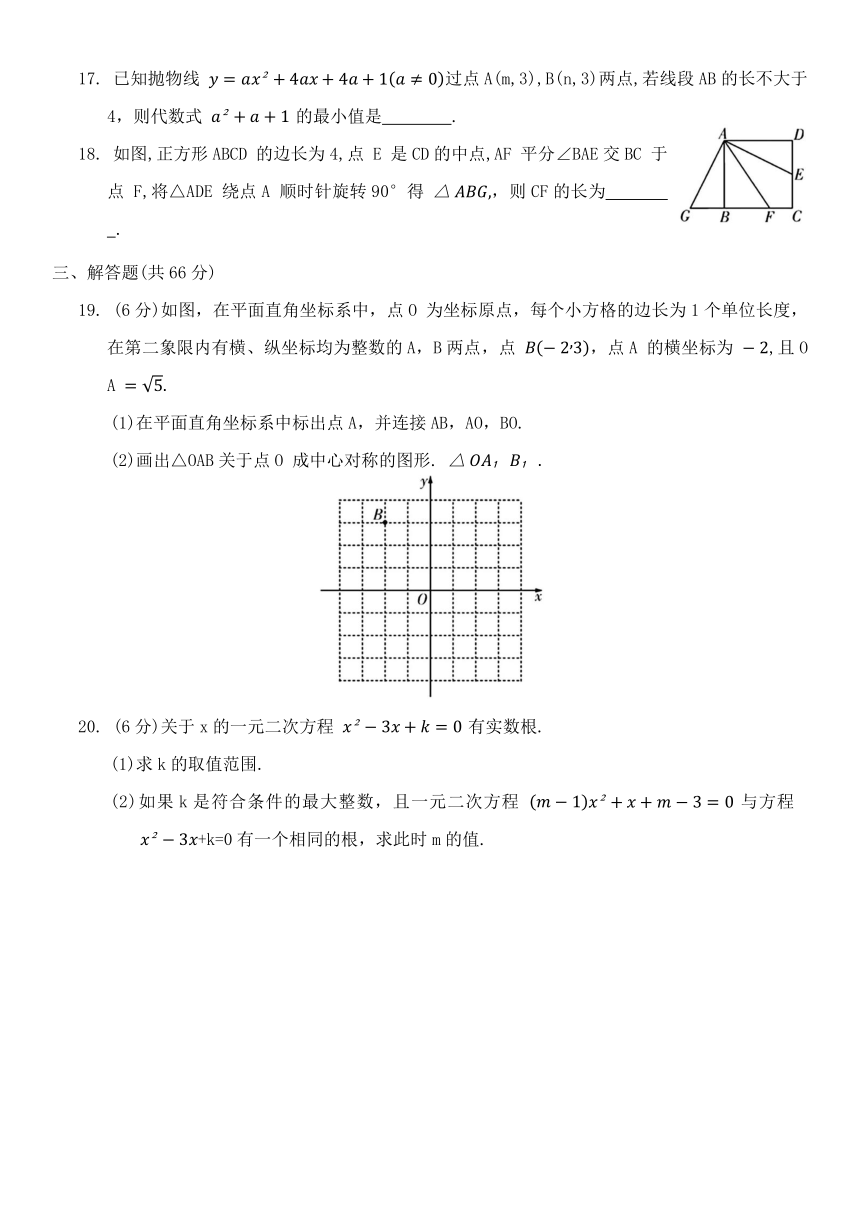
1. 新型冠状病毒肺炎简称“新冠肺炎”,是指新型冠状病毒感染导致的肺炎,预防新型冠状病毒感染的措施是尽量不去人员密集场所,勤洗手,戴口罩,保持室内通风.下列“抗击疫情”的标志中,既是轴对称图形又是中心对称图形的是 ( )
2. x=1是关于x的一元二次方程的解,则2a+4b= ( )
A. -2 B. -3 C. - 1 D. -6
3. 如图,在四边形ABCD中,AB∥CD,AB=2CD,AC交BD于点O,点E,F分别为AO,BO的中点,则下列关于点 O 成中心对称的一组三角形是 ( )
A.△ABO 与△CDO B.△AOD 与△BOC C.△CDO与△EFO D.△ACD与△BCD
4. 若 则代数式 的值为 ( )
A.-1或3 B.1或-3 C. - 1 D.3
5. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB 绕点O 逆时针旋转90°,点 B 的对应点 B'的坐标是 ( )
D.(-3,
6. 在平面直角坐标系中,抛物线y=(x+5)(x-3)经变换后得到抛物线 (x-5),则这个变换可以是 ( )
A.向左平移2个单位 B.向右平移2个单位 C.向左平移8个单位 D.向右平移8个单位
7. 在同一平面直角坐标系中,若抛物线 与 +n关于y轴对称,则符合条件的m,n的值为 ( )
B. m=5,n= -6 C. m= -1,n=6 D. m=1,n= -2
8. 小刚在解关于x的方程 时,只抄对了a=1,b=4,解出其中一个根是x= -1.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是 ( )
A.不存在实数根 B.有两个不相等的实数根
C.有一个根是x=-1 D.有两个相等的实数根
9. 从地面竖直向上先后抛出两个小球,小球的高度h(米)与运动时间t(秒)之间的函数关系式为 若后抛出的小球经过2.5s比先抛出的小球高 ,则抛出两个小球的间隔时间是 ( )
A.1 s B.1. 5s C.2s D.2.5s
10. 抛物线 的对称轴是直线x=-1,且过点(1,0).顶点位于第二象限,其部分图象如图所示,给出以下判断:①ab>0且c<0;②4a-2b+c>0;③8a+c>0;④c=3a-3b;⑤直线y=2x+2与抛物线 两个交点的横坐标分别为x ,x ,则 其中正确的个数有 ( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每小题3分,共24分)
11. 二次函数 的最大值是 .
12. 已知α,β是方程 的两个实数根,则 的值为 .
13. 如图,在△ABC中,AC=BC.将△ABC绕点A逆时针旋转60°,得到△ADE.若AB=2,∠ACB=30°,则线段 CD的长度为 .
14. 已知关于x的一元二次方程 有两个相等的实数根,则 的值等于 .
15. 如图,抛物线 过点( -1,0),(0,2),且顶点在第一象限,设30M=4a+2b+c,则 M 的取值范围是 .
16. 某产品每件的生产成本为50元,原定销售价65元,经市场预测,从现在开始的第一季度销售价格将下降10%,第二季度又将回升5%.若要使半年以后的销售利润不变,设每个季度平均降低成本的百分率为x,根据题意可列方程是 .
已知抛物线 过点A(m,3),B(n,3)两点,若线段AB的长不大于4,则代数式 的最小值是 .
18. 如图,正方形ABCD 的边长为4,点 E 是CD的中点,AF 平分∠BAE交BC 于点 F,将△ADE 绕点A 顺时针旋转90°得 ,则CF的长为 .
三、解答题(共66分)
19. (6分)如图,在平面直角坐标系中,点O 为坐标原点,每个小方格的边长为1个单位长度,在第二象限内有横、纵坐标均为整数的A,B两点,点 ,点A 的横坐标为 ,且OA
(1)在平面直角坐标系中标出点A,并连接AB,AO,BO.
(2)画出△OAB关于点O 成中心对称的图形.
20. (6分)关于x的一元二次方程 有实数根.
(1)求k的取值范围.
(2)如果k是符合条件的最大整数,且一元二次方程 与方程 +k=0有一个相同的根,求此时m的值.
21. (8分)如图,已知正方形ABCD 的边长为 ,点 E 是对角线AC 上一点,连接DE,将线段 DE绕点 D 顺时针旋转 至DF的位置,连接AF,EF.
(1)求证:
(2)当点 E在什么位置时, 的面积最大 并说明理由.
22. (8分)如图,已知A,B,C,D为矩形的四个顶点, ,动点 P,Q分别从A,C两点同时出发,点P以3cm/s的速度向点B 移动,一直到达点B为止,点Q以 的速度向点 D 移动. 点P 停止运动时点 Q 也停止运动.
(1)P,Q两点从出发点出发几秒时,四边形 PBCQ 的面积是
(2)P,Q两点从出发点出发几秒时,点 P,Q间的距离是10cm
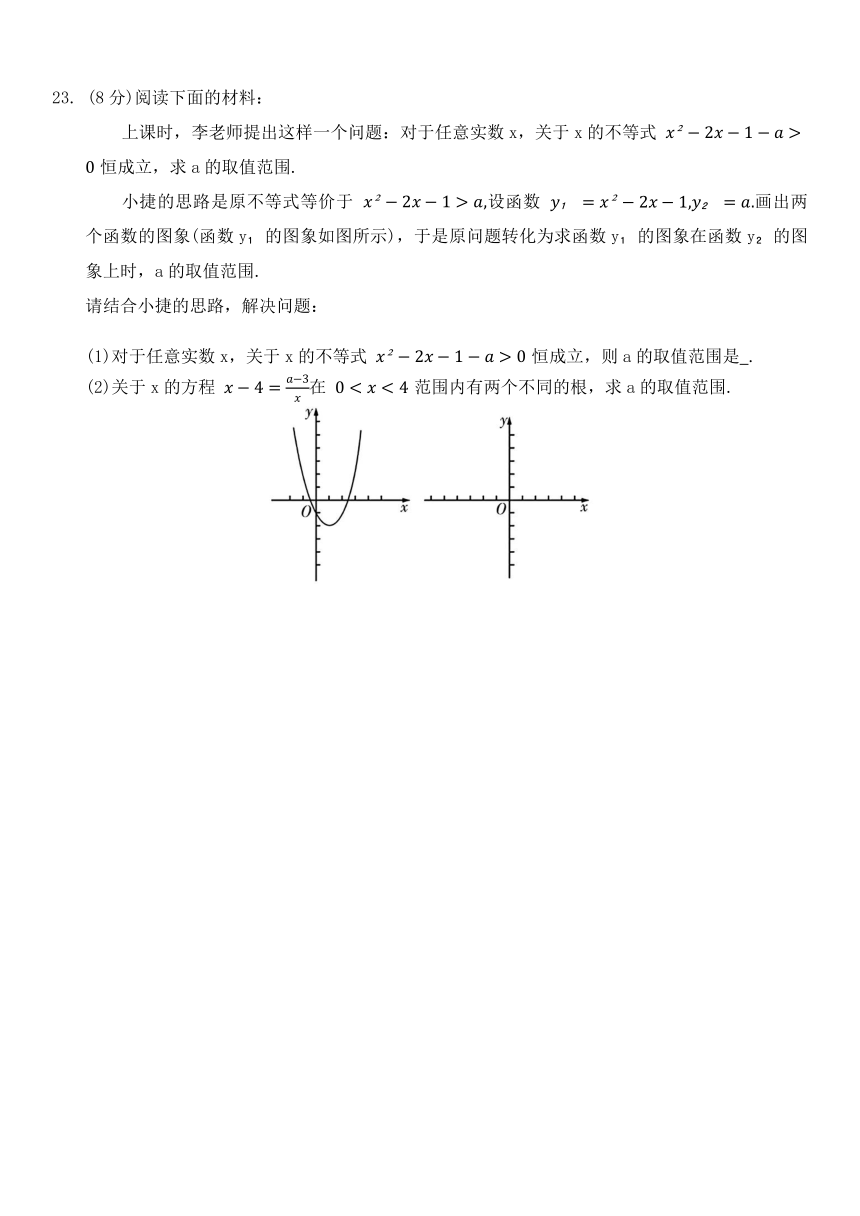
23. (8分)阅读下面的材料:
上课时,李老师提出这样一个问题:对于任意实数x,关于x的不等式 恒成立,求a的取值范围.
小捷的思路是原不等式等价于 设函数 画出两个函数的图象(函数y 的图象如图所示),于是原问题转化为求函数y 的图象在函数y 的图象上时,a的取值范围.
请结合小捷的思路,解决问题:
(1)对于任意实数x,关于x的不等式 恒成立,则a的取值范围是 .
(2)关于x的方程 在 范围内有两个不同的根,求a的取值范围.
24. (8分)已知. 是一张直角三角形纸片,其中 ,小亮将它绕点A逆时针旋转β后得到 AM交直线BD 于点 K.
(1)如图1,当 时,BD 所在直线与线段 FM有怎样的位置关系 请说明理由.
(2)如图2,当 时,求 为等腰直角三角形时的度数.
25. (10分)HW公司2023年使用自主研发生产的“QL”系列甲、乙、丙三类芯片共2800万块,生产了2800万部手机,其中乙类芯片的产量是甲类芯片的2倍,丙类芯片的产量比甲、乙两类芯片产量的和还多400万块.这些“QL”芯片解决了该公司2023年生产的全部手机所需芯片的10%.
(1)求2023年甲类芯片的产量.
(2)HW 公司计划2025年生产的手机全部使用自主研发的“QL”系列芯片.从2024年起逐年扩大“QL”芯片的产量,2024年、2025年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数m%,乙类芯片的产量平均每年增长的百分数比m%小1,丙类芯片的产量每年按相同的数量递增.2023年到2025年,丙类芯片三年的总产量达到1.44亿块.这样,2025年的 HW公司的手机产量比2023年全年的手机产量多10%,求丙类芯片2025年的产量及m的值.
26. (12分)(兴安盟中考)如图,在 中,A,C两点的坐标分别为(4,0), ,抛物线 W经过O,A,C三点,点D 是抛物线 W的顶点.
(1)求抛物线 W的函数解析式及顶点 D 的坐标.
(2)将抛物线 W和 同时先向右平移4个单位长度,再向下平移 个单位长度,得到抛物线l 和 ,在向下平移过程中, 与x轴交于点H, 与OABC 重叠部分的面积记为S,试探究:当m为何值时,S有最大值,并求出S的最大值.
(3)在(2)的条件下,当S取最大值时,设此时抛物线 的顶点为 F,若点 M 是x轴上的动点,点N是抛物线 上的动点,是否存在这样的点M,N,使以D,F,M,N为顶点的四边形是平行四边形 若存在,求出点 M 的坐标;若不存在,请说明理由.
期中综合测试卷
1. B 2. A 3. C 4. D 5. B 6. B 7. D 8. A 9. B 10. D11.8 12.0 13.2 14.2 15. -616.65×(1-10%)×(1+5%)-50(1-x) =65-5017.
19.解:(1)如图所示,点A,AB,AO,BO 即为所求.
(2)如图所示, 即为所求.
20.解:(1)根据题意,得 解得
(2)k的最大整数为2,方程 变形为 =0,解得 ·一元二次方程( 3=0与方程 有一个相同的根,∴当x=1时,m--1+1+m-3=0,解得 当x=2时,4(m-1)+2+m-3=0,解得m=1,而m-1≠0,∴m的值为
21.(1)证明:∵DE 绕点D顺时针旋转90°至 DF 的位置,
∴DE=DF,∠EDF=90°,在正方形ABCD中,CD=AD,∠ADC=90°,
∴ ∠EDF - ∠EDA = ∠ADC - ∠EDA,即 ∠ADF =∠CDE,∴△ADF≌△CDE(SAS).
(2)解:由(1)知△ADF≌△CDE,∴ ∠ECD = ∠DAF =∠CAD=45°,AF=CE,∴∠EAF =90°,设AE =x,∵正方形ABCD 的边长为 故 当x=2,即E在AC中点时,△AEF的面积最大.
22.解:(1)设P,Q两点从出发点出发 ts时,四边形PBCQ 的面积为 Q
整理,得 解得 即P,Q两点从出发点出发5s时,四边形 PBCQ 的面积是:
(2)过点Q作 于点H, l,在 中, 即
解得 即 P,Q两点从出发点出发 或 时,点P,Q间的距离是10 cm.
23.解:
(2)将原方程转化为 设 a,于是原问题转化为求直线 与函数y 在( 范围内的图象有两个不同的交点时a的取值范围.如图,结合图象,可知a的取值范围是
24.解:(1)BD与FM互相垂直,理由如下:
∵∠DAB=90°,∠D=30°,∴∠ABD=90°-∠D=60°,
∴∠KBM=∠ABD=60°,
由旋转的特质,得△ADB≌△AMF,
∴∠D=∠M=30°,∴∠MKB =180°-∠M-∠KBM =180°
-30°-60°=90°,
∴BD与FM互相垂直.
(2)当KA=KD时,∠KAD =∠D°=30°,即β=30°;
当DK=DA时,∠DKA=∠DAK,
即β=75°;
当AK=AD时,∠AKD=∠D=30°,
∴∠KAD=180°-∠AKD-∠D=120°,即β=120°.
综上所述,β的度数为30°或75°或120°.
25.解:(1)设2023年甲类芯片的产量为x万块,由题意,得x+2x+(x+2x) +400=2800,解得x=400.
答:2023年甲类芯片的产量为400万块.
(2)2023年丙类芯片的产量为3x+400 =1600(万块),设丙类芯片的产量每年增加的数量为y万块,则1600 +1600 +y
解得 ∴丙类芯片2025年的产量为 (万块),2023 年 HW 公司手机产量为 (万部),根据题意,得 1 10%),设 得 ,整理,得 解得t=4或 (舍去),
答:丙类芯片2025年的产量为8000万块,m的值为400.
26.解:(1)设抛物线 W的函数解析式为
∵图象经过A(4,0),C(-2,3),
∴抛物线 W的函数解析式为
∴顶点 D 的坐标为(2,-1).
(2)由O(0,0),C(-2,3),得 设直线 的函数解析式为 b,把 代入y= kx+b中,得 m,∵直线 与x轴交于点H, 过点 作 于点E,
∴抛物线开口向下,S有最大值,最大值为 ∴当 时,
(3)存在.理由如下:当 时,由 )得 F(6, ∴抛物线 的函数解析式为 依题意设M(t,0),以D,F,M,N为顶点的四边形是平行四边形,分情况讨论:
①以DF为边时, 点 D,F横坐标之差是4,纵坐标之差是 若点M,N的横纵坐标与之有相同规律,则以D,F,M,N为顶点的四边形是平行四边形,
把 分别代入 中,得 ,
②以DF 为对角线时,以点D,F,M,N为顶点不能构成平行四边形.
综上所述:
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 新型冠状病毒肺炎简称“新冠肺炎”,是指新型冠状病毒感染导致的肺炎,预防新型冠状病毒感染的措施是尽量不去人员密集场所,勤洗手,戴口罩,保持室内通风.下列“抗击疫情”的标志中,既是轴对称图形又是中心对称图形的是 ( )
2. x=1是关于x的一元二次方程的解,则2a+4b= ( )
A. -2 B. -3 C. - 1 D. -6
3. 如图,在四边形ABCD中,AB∥CD,AB=2CD,AC交BD于点O,点E,F分别为AO,BO的中点,则下列关于点 O 成中心对称的一组三角形是 ( )
A.△ABO 与△CDO B.△AOD 与△BOC C.△CDO与△EFO D.△ACD与△BCD
4. 若 则代数式 的值为 ( )
A.-1或3 B.1或-3 C. - 1 D.3
5. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB 绕点O 逆时针旋转90°,点 B 的对应点 B'的坐标是 ( )
D.(-3,
6. 在平面直角坐标系中,抛物线y=(x+5)(x-3)经变换后得到抛物线 (x-5),则这个变换可以是 ( )
A.向左平移2个单位 B.向右平移2个单位 C.向左平移8个单位 D.向右平移8个单位
7. 在同一平面直角坐标系中,若抛物线 与 +n关于y轴对称,则符合条件的m,n的值为 ( )
B. m=5,n= -6 C. m= -1,n=6 D. m=1,n= -2
8. 小刚在解关于x的方程 时,只抄对了a=1,b=4,解出其中一个根是x= -1.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是 ( )
A.不存在实数根 B.有两个不相等的实数根
C.有一个根是x=-1 D.有两个相等的实数根
9. 从地面竖直向上先后抛出两个小球,小球的高度h(米)与运动时间t(秒)之间的函数关系式为 若后抛出的小球经过2.5s比先抛出的小球高 ,则抛出两个小球的间隔时间是 ( )
A.1 s B.1. 5s C.2s D.2.5s
10. 抛物线 的对称轴是直线x=-1,且过点(1,0).顶点位于第二象限,其部分图象如图所示,给出以下判断:①ab>0且c<0;②4a-2b+c>0;③8a+c>0;④c=3a-3b;⑤直线y=2x+2与抛物线 两个交点的横坐标分别为x ,x ,则 其中正确的个数有 ( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每小题3分,共24分)
11. 二次函数 的最大值是 .
12. 已知α,β是方程 的两个实数根,则 的值为 .
13. 如图,在△ABC中,AC=BC.将△ABC绕点A逆时针旋转60°,得到△ADE.若AB=2,∠ACB=30°,则线段 CD的长度为 .
14. 已知关于x的一元二次方程 有两个相等的实数根,则 的值等于 .
15. 如图,抛物线 过点( -1,0),(0,2),且顶点在第一象限,设30M=4a+2b+c,则 M 的取值范围是 .
16. 某产品每件的生产成本为50元,原定销售价65元,经市场预测,从现在开始的第一季度销售价格将下降10%,第二季度又将回升5%.若要使半年以后的销售利润不变,设每个季度平均降低成本的百分率为x,根据题意可列方程是 .
已知抛物线 过点A(m,3),B(n,3)两点,若线段AB的长不大于4,则代数式 的最小值是 .
18. 如图,正方形ABCD 的边长为4,点 E 是CD的中点,AF 平分∠BAE交BC 于点 F,将△ADE 绕点A 顺时针旋转90°得 ,则CF的长为 .
三、解答题(共66分)
19. (6分)如图,在平面直角坐标系中,点O 为坐标原点,每个小方格的边长为1个单位长度,在第二象限内有横、纵坐标均为整数的A,B两点,点 ,点A 的横坐标为 ,且OA
(1)在平面直角坐标系中标出点A,并连接AB,AO,BO.
(2)画出△OAB关于点O 成中心对称的图形.
20. (6分)关于x的一元二次方程 有实数根.
(1)求k的取值范围.
(2)如果k是符合条件的最大整数,且一元二次方程 与方程 +k=0有一个相同的根,求此时m的值.
21. (8分)如图,已知正方形ABCD 的边长为 ,点 E 是对角线AC 上一点,连接DE,将线段 DE绕点 D 顺时针旋转 至DF的位置,连接AF,EF.
(1)求证:
(2)当点 E在什么位置时, 的面积最大 并说明理由.
22. (8分)如图,已知A,B,C,D为矩形的四个顶点, ,动点 P,Q分别从A,C两点同时出发,点P以3cm/s的速度向点B 移动,一直到达点B为止,点Q以 的速度向点 D 移动. 点P 停止运动时点 Q 也停止运动.
(1)P,Q两点从出发点出发几秒时,四边形 PBCQ 的面积是
(2)P,Q两点从出发点出发几秒时,点 P,Q间的距离是10cm
23. (8分)阅读下面的材料:
上课时,李老师提出这样一个问题:对于任意实数x,关于x的不等式 恒成立,求a的取值范围.
小捷的思路是原不等式等价于 设函数 画出两个函数的图象(函数y 的图象如图所示),于是原问题转化为求函数y 的图象在函数y 的图象上时,a的取值范围.
请结合小捷的思路,解决问题:
(1)对于任意实数x,关于x的不等式 恒成立,则a的取值范围是 .
(2)关于x的方程 在 范围内有两个不同的根,求a的取值范围.
24. (8分)已知. 是一张直角三角形纸片,其中 ,小亮将它绕点A逆时针旋转β后得到 AM交直线BD 于点 K.
(1)如图1,当 时,BD 所在直线与线段 FM有怎样的位置关系 请说明理由.
(2)如图2,当 时,求 为等腰直角三角形时的度数.
25. (10分)HW公司2023年使用自主研发生产的“QL”系列甲、乙、丙三类芯片共2800万块,生产了2800万部手机,其中乙类芯片的产量是甲类芯片的2倍,丙类芯片的产量比甲、乙两类芯片产量的和还多400万块.这些“QL”芯片解决了该公司2023年生产的全部手机所需芯片的10%.
(1)求2023年甲类芯片的产量.
(2)HW 公司计划2025年生产的手机全部使用自主研发的“QL”系列芯片.从2024年起逐年扩大“QL”芯片的产量,2024年、2025年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数m%,乙类芯片的产量平均每年增长的百分数比m%小1,丙类芯片的产量每年按相同的数量递增.2023年到2025年,丙类芯片三年的总产量达到1.44亿块.这样,2025年的 HW公司的手机产量比2023年全年的手机产量多10%,求丙类芯片2025年的产量及m的值.
26. (12分)(兴安盟中考)如图,在 中,A,C两点的坐标分别为(4,0), ,抛物线 W经过O,A,C三点,点D 是抛物线 W的顶点.
(1)求抛物线 W的函数解析式及顶点 D 的坐标.
(2)将抛物线 W和 同时先向右平移4个单位长度,再向下平移 个单位长度,得到抛物线l 和 ,在向下平移过程中, 与x轴交于点H, 与OABC 重叠部分的面积记为S,试探究:当m为何值时,S有最大值,并求出S的最大值.
(3)在(2)的条件下,当S取最大值时,设此时抛物线 的顶点为 F,若点 M 是x轴上的动点,点N是抛物线 上的动点,是否存在这样的点M,N,使以D,F,M,N为顶点的四边形是平行四边形 若存在,求出点 M 的坐标;若不存在,请说明理由.
期中综合测试卷
1. B 2. A 3. C 4. D 5. B 6. B 7. D 8. A 9. B 10. D11.8 12.0 13.2 14.2 15. -6
19.解:(1)如图所示,点A,AB,AO,BO 即为所求.
(2)如图所示, 即为所求.
20.解:(1)根据题意,得 解得
(2)k的最大整数为2,方程 变形为 =0,解得 ·一元二次方程( 3=0与方程 有一个相同的根,∴当x=1时,m--1+1+m-3=0,解得 当x=2时,4(m-1)+2+m-3=0,解得m=1,而m-1≠0,∴m的值为
21.(1)证明:∵DE 绕点D顺时针旋转90°至 DF 的位置,
∴DE=DF,∠EDF=90°,在正方形ABCD中,CD=AD,∠ADC=90°,
∴ ∠EDF - ∠EDA = ∠ADC - ∠EDA,即 ∠ADF =∠CDE,∴△ADF≌△CDE(SAS).
(2)解:由(1)知△ADF≌△CDE,∴ ∠ECD = ∠DAF =∠CAD=45°,AF=CE,∴∠EAF =90°,设AE =x,∵正方形ABCD 的边长为 故 当x=2,即E在AC中点时,△AEF的面积最大.
22.解:(1)设P,Q两点从出发点出发 ts时,四边形PBCQ 的面积为 Q
整理,得 解得 即P,Q两点从出发点出发5s时,四边形 PBCQ 的面积是:
(2)过点Q作 于点H, l,在 中, 即
解得 即 P,Q两点从出发点出发 或 时,点P,Q间的距离是10 cm.
23.解:
(2)将原方程转化为 设 a,于是原问题转化为求直线 与函数y 在( 范围内的图象有两个不同的交点时a的取值范围.如图,结合图象,可知a的取值范围是
24.解:(1)BD与FM互相垂直,理由如下:
∵∠DAB=90°,∠D=30°,∴∠ABD=90°-∠D=60°,
∴∠KBM=∠ABD=60°,
由旋转的特质,得△ADB≌△AMF,
∴∠D=∠M=30°,∴∠MKB =180°-∠M-∠KBM =180°
-30°-60°=90°,
∴BD与FM互相垂直.
(2)当KA=KD时,∠KAD =∠D°=30°,即β=30°;
当DK=DA时,∠DKA=∠DAK,
即β=75°;
当AK=AD时,∠AKD=∠D=30°,
∴∠KAD=180°-∠AKD-∠D=120°,即β=120°.
综上所述,β的度数为30°或75°或120°.
25.解:(1)设2023年甲类芯片的产量为x万块,由题意,得x+2x+(x+2x) +400=2800,解得x=400.
答:2023年甲类芯片的产量为400万块.
(2)2023年丙类芯片的产量为3x+400 =1600(万块),设丙类芯片的产量每年增加的数量为y万块,则1600 +1600 +y
解得 ∴丙类芯片2025年的产量为 (万块),2023 年 HW 公司手机产量为 (万部),根据题意,得 1 10%),设 得 ,整理,得 解得t=4或 (舍去),
答:丙类芯片2025年的产量为8000万块,m的值为400.
26.解:(1)设抛物线 W的函数解析式为
∵图象经过A(4,0),C(-2,3),
∴抛物线 W的函数解析式为
∴顶点 D 的坐标为(2,-1).
(2)由O(0,0),C(-2,3),得 设直线 的函数解析式为 b,把 代入y= kx+b中,得 m,∵直线 与x轴交于点H, 过点 作 于点E,
∴抛物线开口向下,S有最大值,最大值为 ∴当 时,
(3)存在.理由如下:当 时,由 )得 F(6, ∴抛物线 的函数解析式为 依题意设M(t,0),以D,F,M,N为顶点的四边形是平行四边形,分情况讨论:
①以DF为边时, 点 D,F横坐标之差是4,纵坐标之差是 若点M,N的横纵坐标与之有相同规律,则以D,F,M,N为顶点的四边形是平行四边形,
把 分别代入 中,得 ,
②以DF 为对角线时,以点D,F,M,N为顶点不能构成平行四边形.
综上所述:
同课章节目录
