人教版数学九年级上册第二十四章 圆 基础复习(二)(含答案)
文档属性
| 名称 | 人教版数学九年级上册第二十四章 圆 基础复习(二)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览

文档简介
第二十四章基础复习(二)
知识点 1 正多边形和圆
正多边形:各边相等,各角也相等的多边形叫做正多边形.
把一个正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形的一边的距离叫做正多边形的边心距.
要作半径为R的正n边形,只要把半径为R的圆n等分,然后顺次连接各部分点即可.
正多边形的有关计算:
①正n边形的每个内角都等于 ②正n边形的每个中心角都等于 ③正n边形的每个外角都等于
1. 如图,正六边形 ABCDEF内接于⊙O,连接BD.则∠CBD的度数是 ( )
B.45° C.60° D.90°
2. 如图,在正六边形ABCDEF中, ,则它的边长是 ( )
A.1 D.2
3. 如图,正五边形ABCDE内接于⊙O,P为 上的一点(点P 不与点D 重合),则∠CPD的度数为 ( )
C.60° D.72°
4. 如图,已知⊙O的内接正六边形ABCDEF的边心距OM=2,则该圆的内接正三角形ACE的面积为 ( )
A.2 B.4
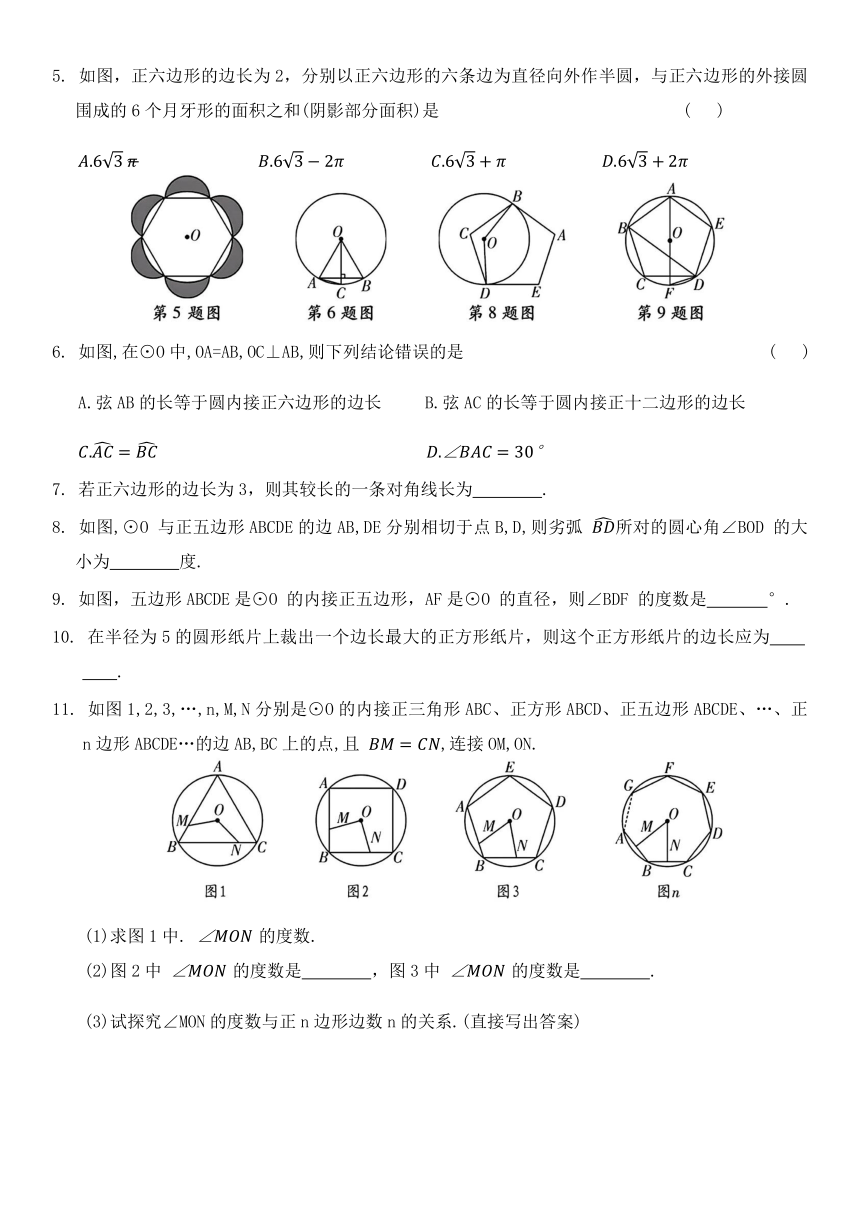
5. 如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是 ( )
6. 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是 ( )
A.弦AB的长等于圆内接正六边形的边长 B.弦AC的长等于圆内接正十二边形的边长
7. 若正六边形的边长为3,则其较长的一条对角线长为 .
8. 如图,⊙O 与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧 所对的圆心角∠BOD 的大小为 度.
9. 如图,五边形ABCDE是⊙O 的内接正五边形,AF是⊙O 的直径,则∠BDF 的度数是 °.
10. 在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .
11. 如图1,2,3,…,n,M,N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB,BC上的点,且 ,连接OM,ON.
(1)求图1中. 的度数.
(2)图2中 的度数是 ,图3中 的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系.(直接写出答案)
知识点2 弧长和扇形面积
弧长公式:
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.扇形的面积公式:S扇形
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.设圆锥的母线长为l,底面圆的半径为r,则圆锥的侧面积为πrl,全面积为πr(r+l).
12. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是(结果保留π) ( )
A.2π B.4π C.12π D.24π
13. 如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4π-8 B.2π C.4π D.8π-8
14. 若扇形的圆心角为 ,半径为6,则该扇形的弧长为 ( )
B.2π C.3π D.6π
15. 如图,在边长为4的正方形ABCD中,以点B 为圆心,AB为半径画弧,交对角线BD于点 E,则图中阴影部分的面积是(结果保留π) ( )
A.8-π B.16-2π C.8-2π
16. 如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则 的长为 ( )
D.2π
17. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是 ( )
B.10 cm C.6cm D.5cm
18. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为 ( )
A.6π D.2π
19. 如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在 上的点 D 处,且表示 的长),若将此扇形OAB 围成一个圆锥,则圆锥的底面半径与母线长的比为 ( )
A.1:3 B.1:π C.1:4 D.2:9
20. 如图,线段AB 经过⊙O 的圆心,AC,BD分别与⊙O 相切于点 C,D.若 ∠A =45°,则 的长度为 ( )
A.π B.2π D.4π
21. 圆锥侧面展开图的圆心角的度数为216°,母线长为5,该圆锥的底面半径为 .
22. 如图,在Rt△ABC中, 以点A 为圆心,以AC 为半径画弧,交AB 于D,则扇形 CAD 的周长是 .(结果保留π)
23. 如图,AC是⊙O 的直径,B,D是⊙O上的点,若⊙O 的半径为3, 则 的长为 .
24. 在1 中, ,把它沿斜边AB 所在直线旋转一周,所得几何体的侧面积是 .(结果保留π)
25. 如图,在平行四边形ABCD中, ,以 CD 为直径的⊙O交AD 于点 E,则图中阴影部分的面积为 .
26. 如图, 内接于⊙O,AD与BC是⊙O 的直径,延长线段AC 至点G,使 连接DG交⊙O于点 E,EF∥AB交AG于点 F.
(1)求证:EF与⊙O 相切.
(2)若 ,求扇形OAC 的面积.
第二十四章基础复习(二)
1. A 2. D 3. B 4. D 5. A 6. D 7.6 8.144 9.54
11.解:(1)如图,连接OB,OC,∵点O是正三角形ABC的中心,
,OC 分别平分∠ABC 和∠ACB,
∵AB =AC,∴ ∠ABC = ∠ACB,∴ ∠OBM =∠OCB,
又∵OB=OC,BM=CN,∴△OBM≌△OCN,∴ ∠BOM =∠CON,
∴ ∠MON=∠BOM+∠BON=∠CON+∠BON=∠BOC= 120°.
(2)90°;72°.
12. C 13. A 14. C 15. C 16. B 17. A 18. A19. D20. B 21.3 22.+2 23.2π
26.(1)证明:如图1,连接OE,∵OD=OE,∴∠D=∠OED.
∵AD=AG,∴∠D=∠G,∴∠OED=∠G,∴OE∥AG,
∵BC是⊙O的直径,∴∠BAC=90°,∵EF∥AB,
∴∠EFG=90°,∵OE∥AG,∴∠OEF=90°,∴OE⊥EF,
∴EF与⊙O 相切.
(2)解:如图 2,连接 OE,过点 O 作 OH ⊥AC 于点 H,
∴CH=2,由(1)知∠HFE=∠OEF=90°,
∴ 四辺形OEFH 是矩形, 在 中,
,
是等边三角形,
知识点 1 正多边形和圆
正多边形:各边相等,各角也相等的多边形叫做正多边形.
把一个正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形的一边的距离叫做正多边形的边心距.
要作半径为R的正n边形,只要把半径为R的圆n等分,然后顺次连接各部分点即可.
正多边形的有关计算:
①正n边形的每个内角都等于 ②正n边形的每个中心角都等于 ③正n边形的每个外角都等于
1. 如图,正六边形 ABCDEF内接于⊙O,连接BD.则∠CBD的度数是 ( )
B.45° C.60° D.90°
2. 如图,在正六边形ABCDEF中, ,则它的边长是 ( )
A.1 D.2
3. 如图,正五边形ABCDE内接于⊙O,P为 上的一点(点P 不与点D 重合),则∠CPD的度数为 ( )
C.60° D.72°
4. 如图,已知⊙O的内接正六边形ABCDEF的边心距OM=2,则该圆的内接正三角形ACE的面积为 ( )
A.2 B.4
5. 如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是 ( )
6. 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是 ( )
A.弦AB的长等于圆内接正六边形的边长 B.弦AC的长等于圆内接正十二边形的边长
7. 若正六边形的边长为3,则其较长的一条对角线长为 .
8. 如图,⊙O 与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧 所对的圆心角∠BOD 的大小为 度.
9. 如图,五边形ABCDE是⊙O 的内接正五边形,AF是⊙O 的直径,则∠BDF 的度数是 °.
10. 在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为 .
11. 如图1,2,3,…,n,M,N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB,BC上的点,且 ,连接OM,ON.
(1)求图1中. 的度数.
(2)图2中 的度数是 ,图3中 的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系.(直接写出答案)
知识点2 弧长和扇形面积
弧长公式:
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.扇形的面积公式:S扇形
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.设圆锥的母线长为l,底面圆的半径为r,则圆锥的侧面积为πrl,全面积为πr(r+l).
12. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是(结果保留π) ( )
A.2π B.4π C.12π D.24π
13. 如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4π-8 B.2π C.4π D.8π-8
14. 若扇形的圆心角为 ,半径为6,则该扇形的弧长为 ( )
B.2π C.3π D.6π
15. 如图,在边长为4的正方形ABCD中,以点B 为圆心,AB为半径画弧,交对角线BD于点 E,则图中阴影部分的面积是(结果保留π) ( )
A.8-π B.16-2π C.8-2π
16. 如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则 的长为 ( )
D.2π
17. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是 ( )
B.10 cm C.6cm D.5cm
18. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为 ( )
A.6π D.2π
19. 如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在 上的点 D 处,且表示 的长),若将此扇形OAB 围成一个圆锥,则圆锥的底面半径与母线长的比为 ( )
A.1:3 B.1:π C.1:4 D.2:9
20. 如图,线段AB 经过⊙O 的圆心,AC,BD分别与⊙O 相切于点 C,D.若 ∠A =45°,则 的长度为 ( )
A.π B.2π D.4π
21. 圆锥侧面展开图的圆心角的度数为216°,母线长为5,该圆锥的底面半径为 .
22. 如图,在Rt△ABC中, 以点A 为圆心,以AC 为半径画弧,交AB 于D,则扇形 CAD 的周长是 .(结果保留π)
23. 如图,AC是⊙O 的直径,B,D是⊙O上的点,若⊙O 的半径为3, 则 的长为 .
24. 在1 中, ,把它沿斜边AB 所在直线旋转一周,所得几何体的侧面积是 .(结果保留π)
25. 如图,在平行四边形ABCD中, ,以 CD 为直径的⊙O交AD 于点 E,则图中阴影部分的面积为 .
26. 如图, 内接于⊙O,AD与BC是⊙O 的直径,延长线段AC 至点G,使 连接DG交⊙O于点 E,EF∥AB交AG于点 F.
(1)求证:EF与⊙O 相切.
(2)若 ,求扇形OAC 的面积.
第二十四章基础复习(二)
1. A 2. D 3. B 4. D 5. A 6. D 7.6 8.144 9.54
11.解:(1)如图,连接OB,OC,∵点O是正三角形ABC的中心,
,OC 分别平分∠ABC 和∠ACB,
∵AB =AC,∴ ∠ABC = ∠ACB,∴ ∠OBM =∠OCB,
又∵OB=OC,BM=CN,∴△OBM≌△OCN,∴ ∠BOM =∠CON,
∴ ∠MON=∠BOM+∠BON=∠CON+∠BON=∠BOC= 120°.
(2)90°;72°.
12. C 13. A 14. C 15. C 16. B 17. A 18. A19. D20. B 21.3 22.+2 23.2π
26.(1)证明:如图1,连接OE,∵OD=OE,∴∠D=∠OED.
∵AD=AG,∴∠D=∠G,∴∠OED=∠G,∴OE∥AG,
∵BC是⊙O的直径,∴∠BAC=90°,∵EF∥AB,
∴∠EFG=90°,∵OE∥AG,∴∠OEF=90°,∴OE⊥EF,
∴EF与⊙O 相切.
(2)解:如图 2,连接 OE,过点 O 作 OH ⊥AC 于点 H,
∴CH=2,由(1)知∠HFE=∠OEF=90°,
∴ 四辺形OEFH 是矩形, 在 中,
,
是等边三角形,
同课章节目录
