人教版数学九年级上册 第二十四章 圆 综合测试卷(含答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十四章 圆 综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览


文档简介
第二十四章综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
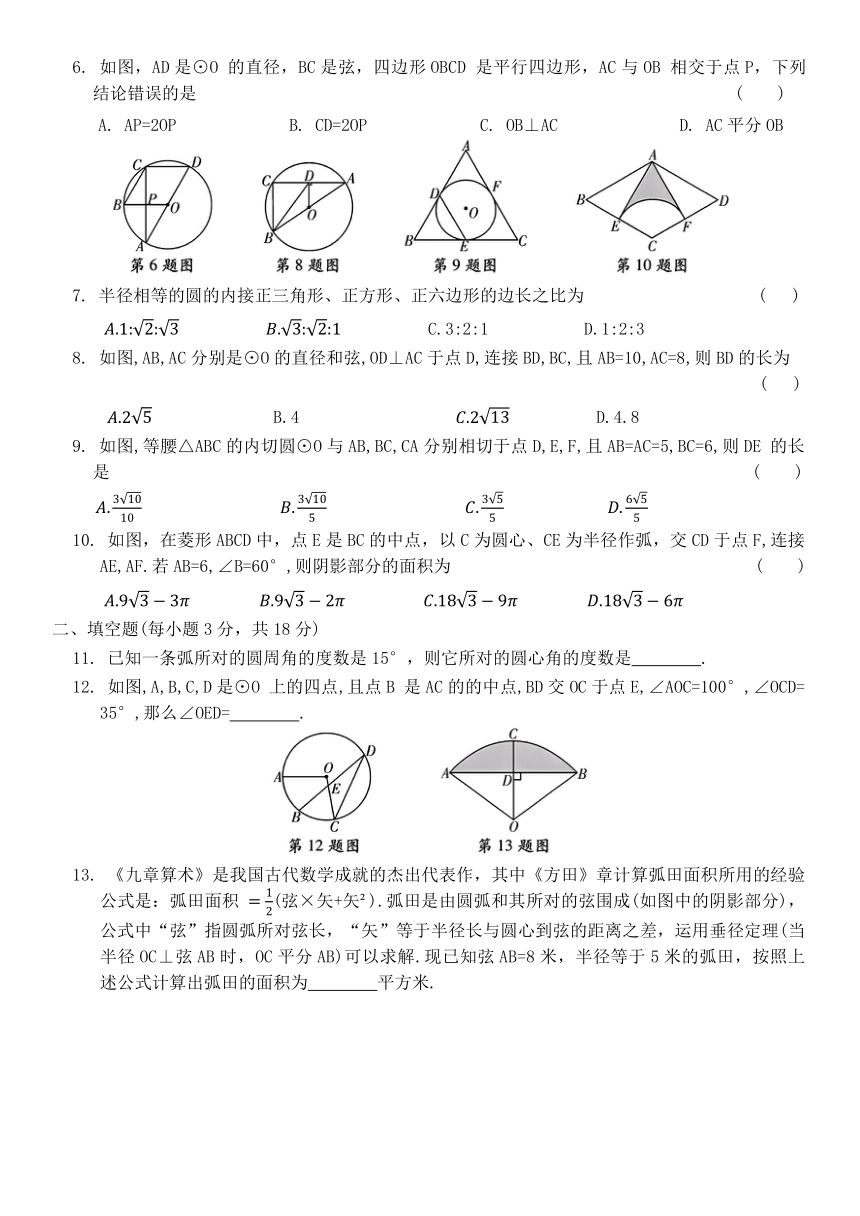
1. 如图,点O为线段BC的中点,点A,C,D 到点O 的距离相等,若∠ABC=40°,则∠ADC的度数是 ( )
A.130° B.140° C.150° D.160°
2. 如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D =80°,则 ∠EAC 的度数为 ( )
A.20° B.25° C.30° D.35°
3. 如图,一条公路的转弯处是一段圆弧 ,点O 是这段弧所在圆的圆心,AB =40 m,点C是 的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为 ( )
A.25m B.24 m C.30 m D.60 m
4. 如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形 OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为 ( )
A.15 cm B.12 cm C.10 cm D. 20cm
5. 如图,直角三角形ABC的内切圆分别与AB,BC 相切于D 点、E点,根据图中标示的长度与角度,求AD的长度为何 ( )
A. B. C. D.
6. 如图,AD是⊙O 的直径,BC是弦,四边形OBCD 是平行四边形,AC与OB 相交于点P,下列结论错误的是 ( )
A. AP=2OP B. CD=2OP C. OB⊥AC D. AC平分OB
7. 半径相等的圆的内接正三角形、正方形、正六边形的边长之比为 ( )
C.3:2:1 D.1:2:3
8. 如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BD,BC,且AB=10,AC=8,则BD的长为 ( )
B.4 D.4.8
9. 如图,等腰△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AB=AC=5,BC=6,则DE 的长是 ( )
10. 如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE,AF.若AB=6,∠B=60°,则阴影部分的面积为 ( )
二、填空题(每小题3分,共18分)
11. 已知一条弧所对的圆周角的度数是15°,则它所对的圆心角的度数是 .
12. 如图,A,B,C,D是⊙O 上的四点,且点B 是AC的的中点,BD交OC于点E,∠AOC=100°,∠OCD=35°,那么∠OED= .
13. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积 (弦×矢+矢 ).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC⊥弦AB时,OC平分AB)可以求解.现已知弦AB=8米,半径等于5米的弧田,按照上述公式计算出弧田的面积为 平方米.
14. 如图,以正方形ABCD 的AB 边向外作正六边形ABEFGH,连接DH.则∠ADH= 度.
15. 如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC上一点,经过C,D两点的⊙O分别交AC,BC于点E,F, 则劣弧 的长为 .
16. 如图,半圆的直径AB=6,点 C 在半圆上,∠BAC=30°, 则阴影部分的面积为 .(结果保留π)
三、解答题(共62分)
17. (10分)如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点 D,与AC交于点E,延长CD,BA 相交于点 F,∠ADF的平分线交AF于点 G.
(1)求证:DG∥CA.
(2)求证:AD=ID.
18. (12分)如图,AB是⊙O的直径,AC与⊙O 交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.
(1)试判断直线 DE 与⊙O 的位置关系,并说明理由.
(2)若⊙O的半径为2,∠BAC=60°,求线段EF的长.
19. (12分)如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点 C 恰好落在⊙O上.
(1)求证:OP∥BC.
(2)过点 C作⊙O 的切线CD,交AP 的延长线于点 D.如果. ,求⊙O的直径.
20. (14分)如图,⊙O 的直径. 半径 D为 上一动点(不包括B,C两点), 垂足分别为E,F.
(1)求EF 的长.
(2)若点 E为OC 的中点,
①求劣弧 CD 的长度.(结果保留π)
②点 P 为直径AB 上一动点,直接写出 的最小值.
21. (14分)如图,BE是⊙O的直径,点A和点D是⊙O上的两点,连接AE,AD,DE,过点A 作射线交 BE 的延长线于点 C,使
(1)求证:AC是⊙O 的切线.
(2)若 ,求阴影部分的面积.
第二十四章综合测试卷
1. B 2. D 3. C 4. A 5. A 6. A 7. B 8. C 9. D 10. A11.30° 12.60°13.10 14.15
17.证明:(1)∵点I是 的内心,
∵ DG平分
∠ :∠ABC,
∴∠1=∠2,∵∠3=∠2,∴∠1=∠3,∴DG∥AC.
(2)由(1)知,∠3 =∠2,∴ ∠3 =∠7,∵点I是△ABC 的内心,
∴∠5=∠6,∵∠4=∠7+∠5,∠DAI=∠3+∠6,
∴∠4 =∠DAI,∴AD=ID.
18.解:(1)直线 DE与⊙O 相切.理由:连接OD.
∵AD平分∠BAC,∴∠OAD=∠CAD,
∵OA=OD,∴∠OAD=∠ODA,
∴∠ODA =∠CAD,∴OD∥AC,∵ DE⊥AC,即∠AED=90°,∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线.
(2)过O作OG⊥AF于G,∴AF=2AG,∵∠BAC=60°,OA=
由(1)知AF∥OD,
∴四边形AODF 是平行四边形,∵OA =OD,
∴四边形AODF是菱形,∴DF∥OA,DF=OA=2,∴∠EFD=∠BAC=60°,
19.(1)证明:∵A 关于 OP 的对称点 C 恰好落在⊙O上,
又
(2)解:如图,连接PC,∵CD为⊙O 的切线,
∴OC⊥CD,∠DCO=90°.又∠D=90°,∴OC∥AD,
∴∠APO=∠COP,
∵∠AOP=∠COP,∴∠APO=∠AOP,∴OA=AP,
∵OA=OP,∴△APO为等边三角形,∴∠AOP=60°,又OP∥BC,∴∠OBC=∠AOP=60°,又OC=OB,
∴ △BCO 为等边三角形,∴∠COB=60°,
∴∠POC=180°-(∠AOP+∠COB)=60°,又OP=OC,
∴△POC为等边三角形,∴∠PCO=60°,PC=OP=OC,又∠OCD=90°,∴ ∠PCD =30°,在 Rt△PCD 中,∠PCD = 又 =4PD=4.即⊙O的直径为4.
20.解:(1)如图,连接OD,∵ ⊙O 的直径AB
=16.∴OA=OB=OD=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴∠DEO=∠EOB =∠DFO=90°,
∴ 四边形 OFDE 是矩形,∴EF=OD=8.
(2)①连接 CD,∵ 点 E 为 OC 的中点,DE⊥OC,∴CE=OE,∠CED=∠OED,∵ DE=DE,∴△DEC≌△DEO,∴CD=OD,∵OC=OD,∴△OCD为等边三角形,
∴∠DOE=60°,
∴劣弧CD的长度为
②延长CO交⊙O于点G,连接DG交AB于点P,则PC+PD的最小值为 12,在Rt△DEG中,∠DEG=90°,∠G=30°,∴DG=2ED,设DE=x,则 解得 的最小值为
21.(1)证明:连接OA,过O作OF⊥AE于F,∴ ∠AFO=90°,∴∠EAO +∠AOF=90°,∵OA =OE,∴ ∠EOF =∠AOF
: ∴AC是⊙O 的切线.
(2)解:
∵∠EAC+∠C=∠AEO,∴∠AEO=2∠EAC,∵OA=OE,
∴∠AEO=∠EAO,∴∠EAO=2∠EAC,
是等边三角形,∴
在
中
∴阴影部分的面积
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 如图,点O为线段BC的中点,点A,C,D 到点O 的距离相等,若∠ABC=40°,则∠ADC的度数是 ( )
A.130° B.140° C.150° D.160°
2. 如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D =80°,则 ∠EAC 的度数为 ( )
A.20° B.25° C.30° D.35°
3. 如图,一条公路的转弯处是一段圆弧 ,点O 是这段弧所在圆的圆心,AB =40 m,点C是 的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为 ( )
A.25m B.24 m C.30 m D.60 m
4. 如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形 OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为 ( )
A.15 cm B.12 cm C.10 cm D. 20cm
5. 如图,直角三角形ABC的内切圆分别与AB,BC 相切于D 点、E点,根据图中标示的长度与角度,求AD的长度为何 ( )
A. B. C. D.
6. 如图,AD是⊙O 的直径,BC是弦,四边形OBCD 是平行四边形,AC与OB 相交于点P,下列结论错误的是 ( )
A. AP=2OP B. CD=2OP C. OB⊥AC D. AC平分OB
7. 半径相等的圆的内接正三角形、正方形、正六边形的边长之比为 ( )
C.3:2:1 D.1:2:3
8. 如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BD,BC,且AB=10,AC=8,则BD的长为 ( )
B.4 D.4.8
9. 如图,等腰△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AB=AC=5,BC=6,则DE 的长是 ( )
10. 如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE,AF.若AB=6,∠B=60°,则阴影部分的面积为 ( )
二、填空题(每小题3分,共18分)
11. 已知一条弧所对的圆周角的度数是15°,则它所对的圆心角的度数是 .
12. 如图,A,B,C,D是⊙O 上的四点,且点B 是AC的的中点,BD交OC于点E,∠AOC=100°,∠OCD=35°,那么∠OED= .
13. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积 (弦×矢+矢 ).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC⊥弦AB时,OC平分AB)可以求解.现已知弦AB=8米,半径等于5米的弧田,按照上述公式计算出弧田的面积为 平方米.
14. 如图,以正方形ABCD 的AB 边向外作正六边形ABEFGH,连接DH.则∠ADH= 度.
15. 如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC上一点,经过C,D两点的⊙O分别交AC,BC于点E,F, 则劣弧 的长为 .
16. 如图,半圆的直径AB=6,点 C 在半圆上,∠BAC=30°, 则阴影部分的面积为 .(结果保留π)
三、解答题(共62分)
17. (10分)如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点 D,与AC交于点E,延长CD,BA 相交于点 F,∠ADF的平分线交AF于点 G.
(1)求证:DG∥CA.
(2)求证:AD=ID.
18. (12分)如图,AB是⊙O的直径,AC与⊙O 交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.
(1)试判断直线 DE 与⊙O 的位置关系,并说明理由.
(2)若⊙O的半径为2,∠BAC=60°,求线段EF的长.
19. (12分)如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点 C 恰好落在⊙O上.
(1)求证:OP∥BC.
(2)过点 C作⊙O 的切线CD,交AP 的延长线于点 D.如果. ,求⊙O的直径.
20. (14分)如图,⊙O 的直径. 半径 D为 上一动点(不包括B,C两点), 垂足分别为E,F.
(1)求EF 的长.
(2)若点 E为OC 的中点,
①求劣弧 CD 的长度.(结果保留π)
②点 P 为直径AB 上一动点,直接写出 的最小值.
21. (14分)如图,BE是⊙O的直径,点A和点D是⊙O上的两点,连接AE,AD,DE,过点A 作射线交 BE 的延长线于点 C,使
(1)求证:AC是⊙O 的切线.
(2)若 ,求阴影部分的面积.
第二十四章综合测试卷
1. B 2. D 3. C 4. A 5. A 6. A 7. B 8. C 9. D 10. A11.30° 12.60°13.10 14.15
17.证明:(1)∵点I是 的内心,
∵ DG平分
∠ :∠ABC,
∴∠1=∠2,∵∠3=∠2,∴∠1=∠3,∴DG∥AC.
(2)由(1)知,∠3 =∠2,∴ ∠3 =∠7,∵点I是△ABC 的内心,
∴∠5=∠6,∵∠4=∠7+∠5,∠DAI=∠3+∠6,
∴∠4 =∠DAI,∴AD=ID.
18.解:(1)直线 DE与⊙O 相切.理由:连接OD.
∵AD平分∠BAC,∴∠OAD=∠CAD,
∵OA=OD,∴∠OAD=∠ODA,
∴∠ODA =∠CAD,∴OD∥AC,∵ DE⊥AC,即∠AED=90°,∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线.
(2)过O作OG⊥AF于G,∴AF=2AG,∵∠BAC=60°,OA=
由(1)知AF∥OD,
∴四边形AODF 是平行四边形,∵OA =OD,
∴四边形AODF是菱形,∴DF∥OA,DF=OA=2,∴∠EFD=∠BAC=60°,
19.(1)证明:∵A 关于 OP 的对称点 C 恰好落在⊙O上,
又
(2)解:如图,连接PC,∵CD为⊙O 的切线,
∴OC⊥CD,∠DCO=90°.又∠D=90°,∴OC∥AD,
∴∠APO=∠COP,
∵∠AOP=∠COP,∴∠APO=∠AOP,∴OA=AP,
∵OA=OP,∴△APO为等边三角形,∴∠AOP=60°,又OP∥BC,∴∠OBC=∠AOP=60°,又OC=OB,
∴ △BCO 为等边三角形,∴∠COB=60°,
∴∠POC=180°-(∠AOP+∠COB)=60°,又OP=OC,
∴△POC为等边三角形,∴∠PCO=60°,PC=OP=OC,又∠OCD=90°,∴ ∠PCD =30°,在 Rt△PCD 中,∠PCD = 又 =4PD=4.即⊙O的直径为4.
20.解:(1)如图,连接OD,∵ ⊙O 的直径AB
=16.∴OA=OB=OD=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴∠DEO=∠EOB =∠DFO=90°,
∴ 四边形 OFDE 是矩形,∴EF=OD=8.
(2)①连接 CD,∵ 点 E 为 OC 的中点,DE⊥OC,∴CE=OE,∠CED=∠OED,∵ DE=DE,∴△DEC≌△DEO,∴CD=OD,∵OC=OD,∴△OCD为等边三角形,
∴∠DOE=60°,
∴劣弧CD的长度为
②延长CO交⊙O于点G,连接DG交AB于点P,则PC+PD的最小值为 12,在Rt△DEG中,∠DEG=90°,∠G=30°,∴DG=2ED,设DE=x,则 解得 的最小值为
21.(1)证明:连接OA,过O作OF⊥AE于F,∴ ∠AFO=90°,∴∠EAO +∠AOF=90°,∵OA =OE,∴ ∠EOF =∠AOF
: ∴AC是⊙O 的切线.
(2)解:
∵∠EAC+∠C=∠AEO,∴∠AEO=2∠EAC,∵OA=OE,
∴∠AEO=∠EAO,∴∠EAO=2∠EAC,
是等边三角形,∴
在
中
∴阴影部分的面积
同课章节目录
