人教版数学九年级上册 期末综合测试卷(一)(含答案)
文档属性
| 名称 | 人教版数学九年级上册 期末综合测试卷(一)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览





文档简介
期末综合测试卷(一)
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
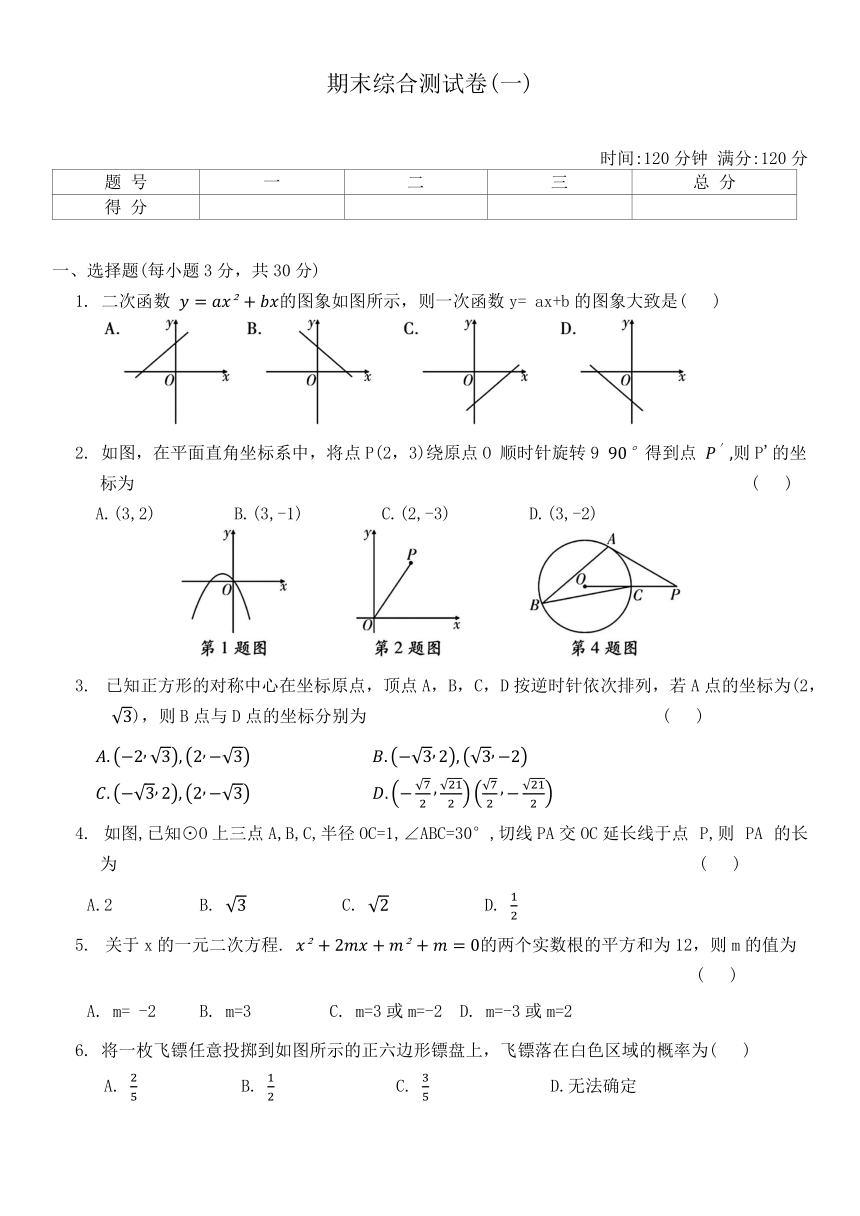
1. 二次函数 的图象如图所示,则一次函数y= ax+b的图象大致是( )
2. 如图,在平面直角坐标系中,将点P(2,3)绕原点O 顺时针旋转9 得到点 则P'的坐标为 ( )
A.(3,2) B.(3,-1) C.(2,-3) D.(3,-2)
3. 已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若A点的坐标为(2, ),则B点与D点的坐标分别为 ( )
4. 如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点 P,则 PA 的长为 ( )
A.2 B. C. D.
5. 关于x的一元二次方程. 的两个实数根的平方和为12,则m的值为 ( )
A. m= -2 B. m=3 C. m=3或m=-2 D. m=-3或m=2
6. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.无法确定
7. 某商店销售富硒农产品,今年1月开始盈利,2月份盈利240000元,4月份盈利290400元,且从2月份到4月份,每月盈利的平均增长率相同,则每月盈利的平均增长率是( )
A.8% B.9% C.10% D.11%
8. 如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2,则图中阴影部分的面积是 ( )
9. 如图,抛物线 与x轴交于A,B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段 PA 的中点,连接OQ.则线段 OQ 的最大值是 ( )
A.3 B. C. D.4
10. 已知抛物线 与y轴交于点A,与直线y= kx(k为任意实数)相交于B,C两点,则下列结论不正确的是 ( )
A.存在实数k,使得△ABC 为等腰三角形
B.存在实数k,使得△ABC的内角中有两角分别为30°和60°
C.任意实数k,使得△ABC 都为直角三角形
D.存在实数k,使得△ABC 为等边三角形
二、填空题(每小题3分,共24分)
11. 若关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是 .
12. 在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有 个.
13. 将抛物线 向左平移 个单位后经过点A(2,2).
14. 在解某个关于x的一元二次方程时,甲看错了一次项的系数,得出的两个根为 ;乙看错了常数项,得出的两根为8,2.则这个方程为 .
15. 某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O 米以内.
16. 如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若 ,则四叶幸运草的周长是 .
17. 如图,等边三角形ABC内有一点 P,分別连接AP,BP,CP,若 10.则
18. 如图, 是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且∠BPC=60°,⊙O 的半径为6,则点 P到AC距离的最大值是 .
三、解答题(共66分)
19. (6分)解下列方程:
20. (7分)如图, 三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出 向左平移6个单位长度后得到的
(2)请画出 关于原点对称的
(3)P为x轴上一动点,当. 有最小值时,求这个最小值.
21. (8分)“一方有难,八方支援”,自新型冠状病毒肺炎疫情发生以来,全国各地的医疗支援队不断集结,陆续前往湖北支援,全国人民众志成城,纷纷慷慨解囊通过捐款支援武汉.小亮和小华想通过网络捐款平台进行资助,以表达自己的爱心,经了解相关捐款信息得知,现网络捐款平台提供四种捐助方式,即“微信支付”、“支付宝”、“QQ 支付”、“银联支付”.假设小亮和小华通过这四种捐助方式进行捐款的可能性相同.
(1)求小亮选择“微信支付”捐款的概率.
(2)请用列表或画树状图法,求小亮和小华恰好都选择“支付宝”或”银联支付”的概率.
22. (8分)如图1,AB 为半圆的直径,点O为圆心,AF为半圆的切线,过半圆上的点 C作 交AF于点D,连接BC.
(1)连接DO,若 ,求证:CD 是半圆的切线.
(2) 如图2,当线段CD与半圆交于点E时,连接AE,AC,判断. 和 的数量关系,并证明你的结论.
23. (9分)(扬州中考)如图,AB是⊙O 的弦,过点O作 OC交AB于 P,
(1)求证:BC是⊙O的切线.
(2)已知 点 Q 是 上的一点.
①求 的度数.
②若 求 的长.
24. (9分)如图1,菱形ABCD的顶点A,D在直线l上, 以点A 为旋转中心将菱形ABCD 顺时针旋转 得到菱形. 交对角线AC于点M,D'交直线l于点 N,连接MN.
(1)当 时,求α的大小.
(2)如图2,对角线. 交AC于点H,交直线l与点 G,延长 交AB 于点 E,连接 EH.当 的周长为2时,求菱形ABCD的周长.
25. (9分)非洲猪瘟疫情爆发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y (元)与月份:,且x为整数)之间满足一次函数关系,如下表所示,每千克猪肉的成本y (元)与月份 ,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x 3 4 5 6
售价y /元 12 14 16 18
(1)求y 与x之间的函数关系式.
(2)求y 与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所获得的利润最大 最大利润是多少元
26. (10分)(长春中考)已知函数(n为常数).
(1)当
①点 P(4,b)在此函数图象上,求b 的值.
②求此函数的最大值.
(2)已知线段AB的两个端点坐标分别为A(2,2),B(4,2),当此函数的图象与线段AB只有一个交点时,直接写出n的取值范围.
(3)当此函数图象上有4个点到x轴的距离等于4,求n的取值范围.
期末综合测试卷(一)
1. D 2. D 3. B 4. B 5. A 6. B 7. C 8. B 9. C10. D 且a≠0 12.7 13.3 14. x -10x+9=0 15.7 17.24+16 18.6+3
19.解:
20.解:(1)如图所示,△A B C 即为所求.
(2)如图所示,△A B C 即为所求.
(3)如图所示,作A点关于x轴的对称点A',A'C交x轴于点P,P点即为所求.当AP+CP 有最小值时,这个最小值为:
21.解:(1)P(小亮选择“微信支付”捐款)
(2)记“微信支付”为A, “支付宝”为B, “QQ支付”为C, “银联支付”为 D.根据题意,画树状图如图:
由树状图可知,共有16种等可能的结果,其中小亮和小华恰好都选择“支付宝”或“银联支付”的结果有2 种,∴P(小亮和小华恰好都选择“支付宝”或“银联支付”)
22.(1)证明:如图1连接OC,∵AF为半圆的切线,AB 为半圆的直径,∴AB⊥AD,∵CD∥AB,BC∥OD,∴四边形 BODC是平行四边形,∴OB=CD,∵OA=OB,∴CD=OA,∴四边形AD-CO是平行四边形,∴OC∥AD,∵CD∥BA,AB⊥AD,∴CD⊥AD,∴OC⊥CD,∴CD是半圆的切线.
(2)解:∠AED+∠ACD=90°.理由:如图2,连接BE,∵AB为半圆的直径,∴∠AEB=90°,∴∠EBA+∠BAE=90°,
∵ ∠DAE + ∠BAE =90°,∴ ∠ABE = ∠DAE,∵ ∠ACE =∠ABE,∴ ∠ACE = ∠DAE,∵ ∠ADE = ∠DAE +∠AED =90°,∴∠AED+∠ACD=90°.
23.(1)证明:连接OB,∵ OA =OB,∴∠OAB
=∠OBA,∵ PC=CB,∴ ∠CPB =∠PBC,
∵OC⊥OA,∴ ∠AOP =90°,∴ ∠OAP +∠APO=90°,∴∠CBP+∠ABO=90°,即∠CBO=90°,∴OB⊥BC,∴BC是⊙O 的切线.
(2)解:①∵∠BAO=25°,∴∠ABO=25°,∴∠AOB=180°-
所对圆心角为 的长
24.解:(1)∵四边形 AB'C'D'是菱形,∴ ,由旋转性质,得 C'D'是等边三角形,∵ MN∥B'D',∴∠C'MN=∠C'B'D'=60°,∠C'NM =∠C'D'B'=60°,∴ △C'MN 是等边三角形,∴C'M=C'N,∴MB'=ND',∵ ∠AB'M =∠AD'N =120°,AB'=AD',∴ △AB'M≌△AD'N(SAS),∴ ∠B'AM = ∠D'AN,∵∠D'AN=∠B'AB =α,∴ ∠B'AM =∠B'AB =α,∵ ∠CAB 即2α=30°,∴α=15°.
(2)∵四边形. 为菱形,∠B'AD'=60°,∴AD'∥B'C',AD'=AB',∴ △AB'D'为等边三角形,. 60°,∴∠AD'B'=60°,∴∠EB'A =∠GD'A.又. AG=∠GAD'+∠B'AG=60°,∴ ∠EAB' =∠GAD',又. AD',∴△AEB'≌△AGD'(ASA),∴EB'=GD',AE=AG,∵AH=AH,∠HAE =∠HAG,∴ △AHE≌△AHG(SAS),∴ EH =GH,∵ △EHB'的周长为2,∴EH+EB'+HB' =B'H+HG+GD'=B'D'=2,∴AB'=AB=2,∴菱形ABCD 的周长为8.
25.解:(1)设y 与x之间的函数关系式为 将(3,12)(4,14)代入,得 解得与x之间的函数关系式为
(2)由题意得,抛物线的顶点坐标为(3,9),∴设y 与x之
间的函数关系式为: 将(5,10)代入 得 解得 与x之间的函数关系式为
(3)由题意,得 w有最大值,∴当 时, 所
以7月份销售每千克猪肉所获得的利润最大,最大利润是每千克7元.
26.解:(1)当 时,
.将P(4,b) 代入 得 ②当. 时,y随x增大而减小,∴当 时有最大值,最大值为5;当: 时,当 时有最大值,最大值为
函数的最大值为
(2)将点(4,2)代入 解得 时,图象与线段AB只有一个交点;将点(2,2)代入y= 解得. 将点(2,2)代入 中, 时图象与线段AB 只有一个交点;综上所述: 时,图象与线段AB 只有一个交点.
时, 函数图象如图实线所示,①如图1 中,当点A 的纵坐标为4时,则有 时,解得 或 (舍去),观察图象可知: 时,满足条件的点恰好有四个,分别是A,B,C,D.②如图2中,观察图象可知,当 时,恰好有四个点满足条件,分别是图中A,B,C,D.
时, 函数图象如图中实线.③如图3 中,当点 A的纵坐标为4时,恰好有四个点满足条件,分别是图中A,B,C,D.则有 时,解得 或 (舍弃).
④如图4中,当n≤-8时,观察图象可知,恰好有四个点满足条件,分别是图中A,B,C,D.
综上所述,函数图象上有4个点到x轴的距离等于4时, -8或 或n=4或n≥8.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 二次函数 的图象如图所示,则一次函数y= ax+b的图象大致是( )
2. 如图,在平面直角坐标系中,将点P(2,3)绕原点O 顺时针旋转9 得到点 则P'的坐标为 ( )
A.(3,2) B.(3,-1) C.(2,-3) D.(3,-2)
3. 已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若A点的坐标为(2, ),则B点与D点的坐标分别为 ( )
4. 如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点 P,则 PA 的长为 ( )
A.2 B. C. D.
5. 关于x的一元二次方程. 的两个实数根的平方和为12,则m的值为 ( )
A. m= -2 B. m=3 C. m=3或m=-2 D. m=-3或m=2
6. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.无法确定
7. 某商店销售富硒农产品,今年1月开始盈利,2月份盈利240000元,4月份盈利290400元,且从2月份到4月份,每月盈利的平均增长率相同,则每月盈利的平均增长率是( )
A.8% B.9% C.10% D.11%
8. 如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2,则图中阴影部分的面积是 ( )
9. 如图,抛物线 与x轴交于A,B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段 PA 的中点,连接OQ.则线段 OQ 的最大值是 ( )
A.3 B. C. D.4
10. 已知抛物线 与y轴交于点A,与直线y= kx(k为任意实数)相交于B,C两点,则下列结论不正确的是 ( )
A.存在实数k,使得△ABC 为等腰三角形
B.存在实数k,使得△ABC的内角中有两角分别为30°和60°
C.任意实数k,使得△ABC 都为直角三角形
D.存在实数k,使得△ABC 为等边三角形
二、填空题(每小题3分,共24分)
11. 若关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是 .
12. 在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有 个.
13. 将抛物线 向左平移 个单位后经过点A(2,2).
14. 在解某个关于x的一元二次方程时,甲看错了一次项的系数,得出的两个根为 ;乙看错了常数项,得出的两根为8,2.则这个方程为 .
15. 某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O 米以内.
16. 如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若 ,则四叶幸运草的周长是 .
17. 如图,等边三角形ABC内有一点 P,分別连接AP,BP,CP,若 10.则
18. 如图, 是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且∠BPC=60°,⊙O 的半径为6,则点 P到AC距离的最大值是 .
三、解答题(共66分)
19. (6分)解下列方程:
20. (7分)如图, 三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出 向左平移6个单位长度后得到的
(2)请画出 关于原点对称的
(3)P为x轴上一动点,当. 有最小值时,求这个最小值.
21. (8分)“一方有难,八方支援”,自新型冠状病毒肺炎疫情发生以来,全国各地的医疗支援队不断集结,陆续前往湖北支援,全国人民众志成城,纷纷慷慨解囊通过捐款支援武汉.小亮和小华想通过网络捐款平台进行资助,以表达自己的爱心,经了解相关捐款信息得知,现网络捐款平台提供四种捐助方式,即“微信支付”、“支付宝”、“QQ 支付”、“银联支付”.假设小亮和小华通过这四种捐助方式进行捐款的可能性相同.
(1)求小亮选择“微信支付”捐款的概率.
(2)请用列表或画树状图法,求小亮和小华恰好都选择“支付宝”或”银联支付”的概率.
22. (8分)如图1,AB 为半圆的直径,点O为圆心,AF为半圆的切线,过半圆上的点 C作 交AF于点D,连接BC.
(1)连接DO,若 ,求证:CD 是半圆的切线.
(2) 如图2,当线段CD与半圆交于点E时,连接AE,AC,判断. 和 的数量关系,并证明你的结论.
23. (9分)(扬州中考)如图,AB是⊙O 的弦,过点O作 OC交AB于 P,
(1)求证:BC是⊙O的切线.
(2)已知 点 Q 是 上的一点.
①求 的度数.
②若 求 的长.
24. (9分)如图1,菱形ABCD的顶点A,D在直线l上, 以点A 为旋转中心将菱形ABCD 顺时针旋转 得到菱形. 交对角线AC于点M,D'交直线l于点 N,连接MN.
(1)当 时,求α的大小.
(2)如图2,对角线. 交AC于点H,交直线l与点 G,延长 交AB 于点 E,连接 EH.当 的周长为2时,求菱形ABCD的周长.
25. (9分)非洲猪瘟疫情爆发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y (元)与月份:,且x为整数)之间满足一次函数关系,如下表所示,每千克猪肉的成本y (元)与月份 ,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x 3 4 5 6
售价y /元 12 14 16 18
(1)求y 与x之间的函数关系式.
(2)求y 与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所获得的利润最大 最大利润是多少元
26. (10分)(长春中考)已知函数(n为常数).
(1)当
①点 P(4,b)在此函数图象上,求b 的值.
②求此函数的最大值.
(2)已知线段AB的两个端点坐标分别为A(2,2),B(4,2),当此函数的图象与线段AB只有一个交点时,直接写出n的取值范围.
(3)当此函数图象上有4个点到x轴的距离等于4,求n的取值范围.
期末综合测试卷(一)
1. D 2. D 3. B 4. B 5. A 6. B 7. C 8. B 9. C10. D 且a≠0 12.7 13.3 14. x -10x+9=0 15.7 17.24+16 18.6+3
19.解:
20.解:(1)如图所示,△A B C 即为所求.
(2)如图所示,△A B C 即为所求.
(3)如图所示,作A点关于x轴的对称点A',A'C交x轴于点P,P点即为所求.当AP+CP 有最小值时,这个最小值为:
21.解:(1)P(小亮选择“微信支付”捐款)
(2)记“微信支付”为A, “支付宝”为B, “QQ支付”为C, “银联支付”为 D.根据题意,画树状图如图:
由树状图可知,共有16种等可能的结果,其中小亮和小华恰好都选择“支付宝”或“银联支付”的结果有2 种,∴P(小亮和小华恰好都选择“支付宝”或“银联支付”)
22.(1)证明:如图1连接OC,∵AF为半圆的切线,AB 为半圆的直径,∴AB⊥AD,∵CD∥AB,BC∥OD,∴四边形 BODC是平行四边形,∴OB=CD,∵OA=OB,∴CD=OA,∴四边形AD-CO是平行四边形,∴OC∥AD,∵CD∥BA,AB⊥AD,∴CD⊥AD,∴OC⊥CD,∴CD是半圆的切线.
(2)解:∠AED+∠ACD=90°.理由:如图2,连接BE,∵AB为半圆的直径,∴∠AEB=90°,∴∠EBA+∠BAE=90°,
∵ ∠DAE + ∠BAE =90°,∴ ∠ABE = ∠DAE,∵ ∠ACE =∠ABE,∴ ∠ACE = ∠DAE,∵ ∠ADE = ∠DAE +∠AED =90°,∴∠AED+∠ACD=90°.
23.(1)证明:连接OB,∵ OA =OB,∴∠OAB
=∠OBA,∵ PC=CB,∴ ∠CPB =∠PBC,
∵OC⊥OA,∴ ∠AOP =90°,∴ ∠OAP +∠APO=90°,∴∠CBP+∠ABO=90°,即∠CBO=90°,∴OB⊥BC,∴BC是⊙O 的切线.
(2)解:①∵∠BAO=25°,∴∠ABO=25°,∴∠AOB=180°-
所对圆心角为 的长
24.解:(1)∵四边形 AB'C'D'是菱形,∴ ,由旋转性质,得 C'D'是等边三角形,∵ MN∥B'D',∴∠C'MN=∠C'B'D'=60°,∠C'NM =∠C'D'B'=60°,∴ △C'MN 是等边三角形,∴C'M=C'N,∴MB'=ND',∵ ∠AB'M =∠AD'N =120°,AB'=AD',∴ △AB'M≌△AD'N(SAS),∴ ∠B'AM = ∠D'AN,∵∠D'AN=∠B'AB =α,∴ ∠B'AM =∠B'AB =α,∵ ∠CAB 即2α=30°,∴α=15°.
(2)∵四边形. 为菱形,∠B'AD'=60°,∴AD'∥B'C',AD'=AB',∴ △AB'D'为等边三角形,. 60°,∴∠AD'B'=60°,∴∠EB'A =∠GD'A.又. AG=∠GAD'+∠B'AG=60°,∴ ∠EAB' =∠GAD',又. AD',∴△AEB'≌△AGD'(ASA),∴EB'=GD',AE=AG,∵AH=AH,∠HAE =∠HAG,∴ △AHE≌△AHG(SAS),∴ EH =GH,∵ △EHB'的周长为2,∴EH+EB'+HB' =B'H+HG+GD'=B'D'=2,∴AB'=AB=2,∴菱形ABCD 的周长为8.
25.解:(1)设y 与x之间的函数关系式为 将(3,12)(4,14)代入,得 解得与x之间的函数关系式为
(2)由题意得,抛物线的顶点坐标为(3,9),∴设y 与x之
间的函数关系式为: 将(5,10)代入 得 解得 与x之间的函数关系式为
(3)由题意,得 w有最大值,∴当 时, 所
以7月份销售每千克猪肉所获得的利润最大,最大利润是每千克7元.
26.解:(1)当 时,
.将P(4,b) 代入 得 ②当. 时,y随x增大而减小,∴当 时有最大值,最大值为5;当: 时,当 时有最大值,最大值为
函数的最大值为
(2)将点(4,2)代入 解得 时,图象与线段AB只有一个交点;将点(2,2)代入y= 解得. 将点(2,2)代入 中, 时图象与线段AB 只有一个交点;综上所述: 时,图象与线段AB 只有一个交点.
时, 函数图象如图实线所示,①如图1 中,当点A 的纵坐标为4时,则有 时,解得 或 (舍去),观察图象可知: 时,满足条件的点恰好有四个,分别是A,B,C,D.②如图2中,观察图象可知,当 时,恰好有四个点满足条件,分别是图中A,B,C,D.
时, 函数图象如图中实线.③如图3 中,当点 A的纵坐标为4时,恰好有四个点满足条件,分别是图中A,B,C,D.则有 时,解得 或 (舍弃).
④如图4中,当n≤-8时,观察图象可知,恰好有四个点满足条件,分别是图中A,B,C,D.
综上所述,函数图象上有4个点到x轴的距离等于4时, -8或 或n=4或n≥8.
同课章节目录
