人教版数学九年级上册 期末综合测试卷(二)(含答案)
文档属性
| 名称 | 人教版数学九年级上册 期末综合测试卷(二)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 18:58:55 | ||
图片预览





文档简介
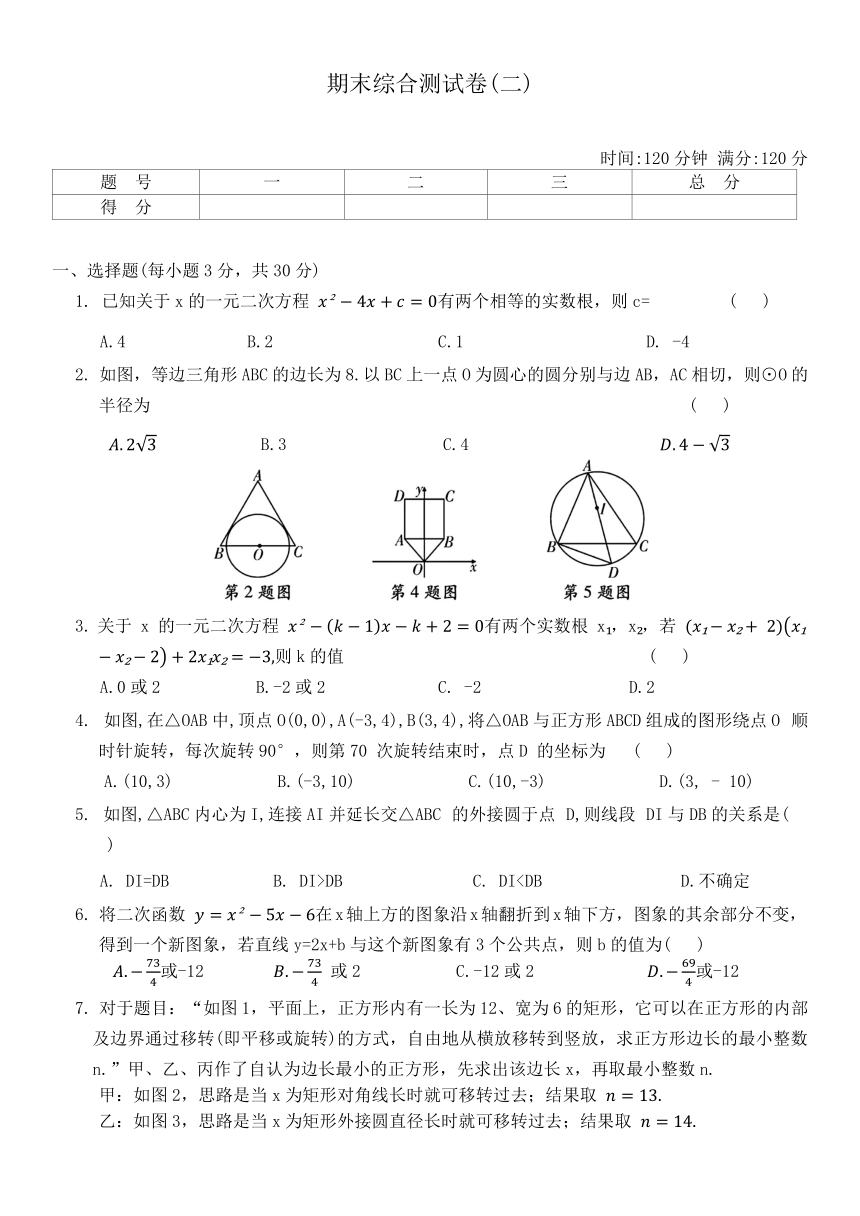
期末综合测试卷(二)
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 已知关于x的一元二次方程 有两个相等的实数根,则c= ( )
A.4 B.2 C.1 D. -4
2. 如图,等边三角形ABC的边长为8.以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为 ( )
B.3 C.4
关于x的一元二次方程 有两个实数根x ,x ,若 则k的值 ( )
A.0或2 B.-2或2 C. -2 D.2
4. 如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O 顺时针旋转,每次旋转90°,则第70 次旋转结束时,点D 的坐标为 ( )
A.(10,3) B.(-3,10) C.(10,-3) D.(3, - 10)
5. 如图,△ABC内心为I,连接AI并延长交△ABC 的外接圆于点 D,则线段 DI与DB的关系是( )
A. DI=DB B. DI>DB C. DI6. 将二次函数 在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )
或-12 或2 C.-12或2 或-12
7. 对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n.”甲、乙、丙作了自认为边长最小的正方形,先求出该边长x,再取最小整数n.
甲:如图2,思路是当x为矩形对角线长时就可移转过去;结果取
乙:如图3,思路是当x为矩形外接圆直径长时就可移转过去;结果取
丙:如图4,思路是当x为矩形的长与宽之和的 倍时就可移转过去;结果取
下列正确的是 ( )
A.甲的思路错,他的n值对 B.乙的思路和他的n值都对
C.甲和丙的n值都对 D.甲、乙的思路都错,而丙的思路对
8. 甲、乙是两个不透明的纸箱,甲中有三张标有数字 1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a,从乙中任取一张卡片,将其数字记为b.若a,b能使关于x的一元二次方程 有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为( )
A. B. C.
9. 如图,⊙O中,AB=AC.∠ACB=75°,BC=2.则阴影部分的面积是 ( )
10. 如图,抛物线 与x轴交于点( -3,0),其对称轴为直线 结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大;④一元二次方程 的两根分别为 ⑥若m,n(m2,其中正确的结论有( )
A.3个 B.4个 C.5个 D.6个
二、填空题(每小题3分,共24分)
11. 一元二次方程(x-3)(x-2)=0的根是 .
12. 将边长为l 的正方形 ABCD 绕点 C 按顺时针方向旋转得到FECG的位置(如图),使得点D落在对角线CF上,EF与AD 相交于点H,则 (结果保留根号)
13. 用一块圆心角为 的扇形铁皮,围成一个底面直径为10cm的圆锥形工件的侧面,那么这个圆锥的高是 cm.
14. 已知a,b均为非零实数,关于x的一元二次方程 两个根为m,n,且 则a的值为 .
15. 如图,有两个转盘A,B,在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘A,B,当转盘停止转动时,若事件“指针都落在标有数字1的扇形区域内”的概率是 ,则转盘B 中标有数字1的扇形的圆心角的度数是 度.
16. 如图,CD为⊙O 的直径,弦, ,垂足为E, 则弦AF的长度为 .
17. 已知二次函数的图象经过点P(2,2),顶点为O(0,0),将该图象向右平移,当它再次经过点 P时,所得抛物线的函数关系式为 .
18. 如图,直线 与抛物线 交于A,B两点,点P是y轴上的一个动点,当 的周长最小时,
三、解答题(共66分)
19. (6分)在如图所示: 的正方形网格中,A(2,0),B(3,2),C(4,2),请按要求解答下列问题:
(1)将 向右平移4个单位长度得到 请画出 并写出点. 的坐标.
(2)将 绕点 C(4,2)顺时针旋转 得到 请画出 并写出点. 的坐标.
(3)将 绕点Q 旋转 可以和 完全重合,请直接写出点 Q 的坐标.
20. (8分)关于x的方程
(1)求证:无论 k为何值,方程总有实数根.
(2)设x ,x 是方程 的两个根,记 S的值能为2 吗 若能,求出此时k的值;若不能,请说明理由.
21. (8分)图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点 C 处的概率是 .
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
22.(8分)在平面内,给定不在同一条直线上的点A,B,C,如图所示,点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,的平分线交图形G于点D,连接AD,CD.
(1)求证:
(2)过点D作 垂足为E,作 ,垂足为 F,延长 DF 交图形G于点 M,连接CM.若 .求直线 DE 与图形G的公共点个数.
23. (8分)一次函数 与二次函数 的图象的一个交点坐标为(1,2)另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值.
(2)过点A(0,m)(024. (8分)(镇江中考)【材料阅读】
地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1 中的⊙O).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角α的大小是变化的.
【实际应用】
观测点A 在图1 所示的⊙O上,现在利用这个工具尺在点A处测得α为31°,在点A 所在子午线往北的另一个观测点B,用同样的工具尺测得α为67°. PQ是⊙O的直径,PQ⊥ON.
(1)求∠POB 的度数.
(2)已知OP=6400km,求这两个观测点之间的距离即⊙O上 的长.(π取3.1)
25. (10分)某文明小区有50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都入住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90000元,问该小区共有多少套80平方米的住宅
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次活动.为提高大家的积极性,6月份准备把活动一升级为活动二:“垃圾分类抵扣物管费”,同时终止活动一.经调查与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加2a%,每户物管费将会减少 6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加6a%,每户物管费将会减少 这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少 求a的值.
26. (10分)如图,抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点 C,点D 是抛物线的顶点.
(1)求抛物线的解析式.
(2)点N是y轴负半轴上的一点,且 点 Q 在对称轴右侧的抛物线上运动,连接QO,QO 与抛物线的对称轴交于点 M,连接MN,当MN平分. 时,求点 Q 的坐标.
(3)直线BC 交对称轴于点E,P是坐标平面内一点,请直接写出 与 全等时点 P的坐标.
期末综合测试卷(二)
1. A2. A3. D4. D 5. A6. A7. B 8. C 9. A 10. C 15.80
19.解:(1)如图所示, 即为所求,点. 的坐标为(6,0).
(2)如图所示, 即为所求,点 的坐标为(2,4).
(3)如图所示,点 Q 的坐标为(6,4).
20.解:(1)当 时,原方程可化为 解得 此时该方程有实数根;
当 时,方程是一元二次方程.
时,方程总有两个不相等的实数根.综上所述,无论k为何值,方程总有实数根.
(2)由题意知, 由根与系数的关系可知,
若 则
即
将 代入上式,整理得
解得 (舍去),
∴S的值能为2,此时
21.解:(1)随机掷一次骰子,向上三个面的数字可能是1,2,3;1,2,4;1,3,4;2,3,4.对应的数字之和是6,7,8,9,则从A点
开始,棋子可跳动之A,B,C,D四个位置.则棋子跳动到点 C处的概率是 故答案为:
(2)随机掷两次骰子,棋子最终是跳动到点 C处的数字之和是14,列表如下:
第一次 第二次~ 9 8 7 6
9 (9,9) (8,9) (7,9) (6,9)
8 (9,8) (8,8) (7,8) (6,8)
7 (9,7) (8,7) (7,7) (6,7)
6 (9,6) (8,6) (7,6) (6,6)
共有16种等可能的结果,和为14的结果有3种,所以棋子最终跳动到点 C处的概率为
22.(1)证明:如图,∵到点O的距离等于a的所有点组成图形G,且点O到A,B,C的距离均等于a,∴图形 G为 的外接圆 ⊙O,
∵ BD 平分 ∠ABC,∴
(2)解:如图,连接OD,∵AD =CM,AD =CD,
∴ CD =CM,∵DM⊥BC,∴BC垂直平分 DM,∴BC 为直径,∴ ∠BAC = DE,∴DE为⊙O的切线,∴直线 DE 与图形 G的公共点个数为1.
23.解:(1)∵点(1,2)在一次函数y= kx+4的图象上,∴2=k+4,即k=-2.
∵一次函数y= - 2x+4 与二次函数 图象的另一个交点是该二次函数图象的顶点,
∴(0,c)在一次函数y=-2x+4的图象上,即c=4.
∵点(1,2)也在二次函数 的图象上,
∴2=a+c,∴a= -2.
(2)∵点A的坐标为(0,m)(0∴可设点B 的坐标为( 由对称性得点 C 的坐标为
∵点B 在二次函数 的图象上,
即
∴m=1时,W有最小值7.
24.解:(1)连接OB,设点 B的切线CB交ON 延长线于点 E,HD⊥BC 于点D,CH⊥BH交 BC 于点 C,如图所示.则∠DHC =67°,∵∠HBD +∠BHD=∠BHD+∠DHC=90°,∴∠HBD = ∠DHC = 67°,∵ ON ∥BH,∴ ∠BEO = ∠HBD = 67°,∴∠BOE=90°-67°=23°,∵PQ⊥ON,∴∠POE=90°,∠POB=90°-23°=67°.
(2)连接OA,同(1)可证∠POA=31°,∴∠AOB =∠POB -
25.(1)解:设该小区有x套80平方米住宅,则50平方米住宅有2x套,由题意,得2(50×2x+80x)=90000,解得x=250.答:该小区共有250套80平方米的住宅.
(2)参与活动一:50平方米住宅每户所交物管费为100 元,有500×40%=200(户)参与活动一,80平方米住宅每户所交物管费为160元,有250×20% =50(户)参与活动一;
参与活动二:50平方米住宅每户所交物管费为 元,有 户参与活动二:80平方米住宅每户所交物管费为 元,有 户参与活动
二.由题意,得 令 化简得 (舍), 即
答:a的值为50.
26.解:(1)∵抛物线 经过 ,B(3,0)两点, 解得 抛物线的解析式为y
(2)如图,设对称轴与x轴交于点 H,抛物线的对称轴为
∵ MN 平分 又 在 中,
①当 时,直线OM解析式为:y=x,依题意,得 解得 点 Q 在对称轴右侧的抛物线上运动, Q 点纵坐标
②当. 时,直线OM解析式为:y= -x,同理可求 综上所述:点Q 的坐标为:
(3)由题意可知:
∵直线BC经过B(3,0),C(0,-3),∴直线 BC 解析式为y ∵抛物线对称轴为 ,直线BC交对称轴于点 E,
∴ E 点坐标为 设P点坐标为(x,y),则 若 与 全等,有两种情况:( 即
解得 或 即 P 点坐标为
即
解得 或 即 P点坐标为 故若 与 全等,P点有四个,坐标为
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 已知关于x的一元二次方程 有两个相等的实数根,则c= ( )
A.4 B.2 C.1 D. -4
2. 如图,等边三角形ABC的边长为8.以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为 ( )
B.3 C.4
关于x的一元二次方程 有两个实数根x ,x ,若 则k的值 ( )
A.0或2 B.-2或2 C. -2 D.2
4. 如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O 顺时针旋转,每次旋转90°,则第70 次旋转结束时,点D 的坐标为 ( )
A.(10,3) B.(-3,10) C.(10,-3) D.(3, - 10)
5. 如图,△ABC内心为I,连接AI并延长交△ABC 的外接圆于点 D,则线段 DI与DB的关系是( )
A. DI=DB B. DI>DB C. DI
或-12 或2 C.-12或2 或-12
7. 对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n.”甲、乙、丙作了自认为边长最小的正方形,先求出该边长x,再取最小整数n.
甲:如图2,思路是当x为矩形对角线长时就可移转过去;结果取
乙:如图3,思路是当x为矩形外接圆直径长时就可移转过去;结果取
丙:如图4,思路是当x为矩形的长与宽之和的 倍时就可移转过去;结果取
下列正确的是 ( )
A.甲的思路错,他的n值对 B.乙的思路和他的n值都对
C.甲和丙的n值都对 D.甲、乙的思路都错,而丙的思路对
8. 甲、乙是两个不透明的纸箱,甲中有三张标有数字 1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a,从乙中任取一张卡片,将其数字记为b.若a,b能使关于x的一元二次方程 有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为( )
A. B. C.
9. 如图,⊙O中,AB=AC.∠ACB=75°,BC=2.则阴影部分的面积是 ( )
10. 如图,抛物线 与x轴交于点( -3,0),其对称轴为直线 结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大;④一元二次方程 的两根分别为 ⑥若m,n(m
A.3个 B.4个 C.5个 D.6个
二、填空题(每小题3分,共24分)
11. 一元二次方程(x-3)(x-2)=0的根是 .
12. 将边长为l 的正方形 ABCD 绕点 C 按顺时针方向旋转得到FECG的位置(如图),使得点D落在对角线CF上,EF与AD 相交于点H,则 (结果保留根号)
13. 用一块圆心角为 的扇形铁皮,围成一个底面直径为10cm的圆锥形工件的侧面,那么这个圆锥的高是 cm.
14. 已知a,b均为非零实数,关于x的一元二次方程 两个根为m,n,且 则a的值为 .
15. 如图,有两个转盘A,B,在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘A,B,当转盘停止转动时,若事件“指针都落在标有数字1的扇形区域内”的概率是 ,则转盘B 中标有数字1的扇形的圆心角的度数是 度.
16. 如图,CD为⊙O 的直径,弦, ,垂足为E, 则弦AF的长度为 .
17. 已知二次函数的图象经过点P(2,2),顶点为O(0,0),将该图象向右平移,当它再次经过点 P时,所得抛物线的函数关系式为 .
18. 如图,直线 与抛物线 交于A,B两点,点P是y轴上的一个动点,当 的周长最小时,
三、解答题(共66分)
19. (6分)在如图所示: 的正方形网格中,A(2,0),B(3,2),C(4,2),请按要求解答下列问题:
(1)将 向右平移4个单位长度得到 请画出 并写出点. 的坐标.
(2)将 绕点 C(4,2)顺时针旋转 得到 请画出 并写出点. 的坐标.
(3)将 绕点Q 旋转 可以和 完全重合,请直接写出点 Q 的坐标.
20. (8分)关于x的方程
(1)求证:无论 k为何值,方程总有实数根.
(2)设x ,x 是方程 的两个根,记 S的值能为2 吗 若能,求出此时k的值;若不能,请说明理由.
21. (8分)图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点 C 处的概率是 .
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
22.(8分)在平面内,给定不在同一条直线上的点A,B,C,如图所示,点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,的平分线交图形G于点D,连接AD,CD.
(1)求证:
(2)过点D作 垂足为E,作 ,垂足为 F,延长 DF 交图形G于点 M,连接CM.若 .求直线 DE 与图形G的公共点个数.
23. (8分)一次函数 与二次函数 的图象的一个交点坐标为(1,2)另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值.
(2)过点A(0,m)(0
地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1 中的⊙O).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角α的大小是变化的.
【实际应用】
观测点A 在图1 所示的⊙O上,现在利用这个工具尺在点A处测得α为31°,在点A 所在子午线往北的另一个观测点B,用同样的工具尺测得α为67°. PQ是⊙O的直径,PQ⊥ON.
(1)求∠POB 的度数.
(2)已知OP=6400km,求这两个观测点之间的距离即⊙O上 的长.(π取3.1)
25. (10分)某文明小区有50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都入住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90000元,问该小区共有多少套80平方米的住宅
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次活动.为提高大家的积极性,6月份准备把活动一升级为活动二:“垃圾分类抵扣物管费”,同时终止活动一.经调查与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加2a%,每户物管费将会减少 6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加6a%,每户物管费将会减少 这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少 求a的值.
26. (10分)如图,抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点 C,点D 是抛物线的顶点.
(1)求抛物线的解析式.
(2)点N是y轴负半轴上的一点,且 点 Q 在对称轴右侧的抛物线上运动,连接QO,QO 与抛物线的对称轴交于点 M,连接MN,当MN平分. 时,求点 Q 的坐标.
(3)直线BC 交对称轴于点E,P是坐标平面内一点,请直接写出 与 全等时点 P的坐标.
期末综合测试卷(二)
1. A2. A3. D4. D 5. A6. A7. B 8. C 9. A 10. C 15.80
19.解:(1)如图所示, 即为所求,点. 的坐标为(6,0).
(2)如图所示, 即为所求,点 的坐标为(2,4).
(3)如图所示,点 Q 的坐标为(6,4).
20.解:(1)当 时,原方程可化为 解得 此时该方程有实数根;
当 时,方程是一元二次方程.
时,方程总有两个不相等的实数根.综上所述,无论k为何值,方程总有实数根.
(2)由题意知, 由根与系数的关系可知,
若 则
即
将 代入上式,整理得
解得 (舍去),
∴S的值能为2,此时
21.解:(1)随机掷一次骰子,向上三个面的数字可能是1,2,3;1,2,4;1,3,4;2,3,4.对应的数字之和是6,7,8,9,则从A点
开始,棋子可跳动之A,B,C,D四个位置.则棋子跳动到点 C处的概率是 故答案为:
(2)随机掷两次骰子,棋子最终是跳动到点 C处的数字之和是14,列表如下:
第一次 第二次~ 9 8 7 6
9 (9,9) (8,9) (7,9) (6,9)
8 (9,8) (8,8) (7,8) (6,8)
7 (9,7) (8,7) (7,7) (6,7)
6 (9,6) (8,6) (7,6) (6,6)
共有16种等可能的结果,和为14的结果有3种,所以棋子最终跳动到点 C处的概率为
22.(1)证明:如图,∵到点O的距离等于a的所有点组成图形G,且点O到A,B,C的距离均等于a,∴图形 G为 的外接圆 ⊙O,
∵ BD 平分 ∠ABC,∴
(2)解:如图,连接OD,∵AD =CM,AD =CD,
∴ CD =CM,∵DM⊥BC,∴BC垂直平分 DM,∴BC 为直径,∴ ∠BAC = DE,∴DE为⊙O的切线,∴直线 DE 与图形 G的公共点个数为1.
23.解:(1)∵点(1,2)在一次函数y= kx+4的图象上,∴2=k+4,即k=-2.
∵一次函数y= - 2x+4 与二次函数 图象的另一个交点是该二次函数图象的顶点,
∴(0,c)在一次函数y=-2x+4的图象上,即c=4.
∵点(1,2)也在二次函数 的图象上,
∴2=a+c,∴a= -2.
(2)∵点A的坐标为(0,m)(0
∵点B 在二次函数 的图象上,
即
∴m=1时,W有最小值7.
24.解:(1)连接OB,设点 B的切线CB交ON 延长线于点 E,HD⊥BC 于点D,CH⊥BH交 BC 于点 C,如图所示.则∠DHC =67°,∵∠HBD +∠BHD=∠BHD+∠DHC=90°,∴∠HBD = ∠DHC = 67°,∵ ON ∥BH,∴ ∠BEO = ∠HBD = 67°,∴∠BOE=90°-67°=23°,∵PQ⊥ON,∴∠POE=90°,∠POB=90°-23°=67°.
(2)连接OA,同(1)可证∠POA=31°,∴∠AOB =∠POB -
25.(1)解:设该小区有x套80平方米住宅,则50平方米住宅有2x套,由题意,得2(50×2x+80x)=90000,解得x=250.答:该小区共有250套80平方米的住宅.
(2)参与活动一:50平方米住宅每户所交物管费为100 元,有500×40%=200(户)参与活动一,80平方米住宅每户所交物管费为160元,有250×20% =50(户)参与活动一;
参与活动二:50平方米住宅每户所交物管费为 元,有 户参与活动二:80平方米住宅每户所交物管费为 元,有 户参与活动
二.由题意,得 令 化简得 (舍), 即
答:a的值为50.
26.解:(1)∵抛物线 经过 ,B(3,0)两点, 解得 抛物线的解析式为y
(2)如图,设对称轴与x轴交于点 H,抛物线的对称轴为
∵ MN 平分 又 在 中,
①当 时,直线OM解析式为:y=x,依题意,得 解得 点 Q 在对称轴右侧的抛物线上运动, Q 点纵坐标
②当. 时,直线OM解析式为:y= -x,同理可求 综上所述:点Q 的坐标为:
(3)由题意可知:
∵直线BC经过B(3,0),C(0,-3),∴直线 BC 解析式为y ∵抛物线对称轴为 ,直线BC交对称轴于点 E,
∴ E 点坐标为 设P点坐标为(x,y),则 若 与 全等,有两种情况:( 即
解得 或 即 P 点坐标为
即
解得 或 即 P点坐标为 故若 与 全等,P点有四个,坐标为
同课章节目录
