人教版数学九年级上册 24.4弧长和扇形面积 课件(共17张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.4弧长和扇形面积 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 21:16:28 | ||
图片预览



文档简介
(共17张PPT)
第二十四章 圆
24.4弧长和扇形面积
学习目标
重点
难点
会利用弧长和扇形面积的计算公式进行计算.
探索弧长计算方法和扇形面积计算方法.
(1) 理解弧长和扇形面积公式的探求过程.
(2)会利用弧长和扇形面积的计算公式进行计算.
情境引入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
探究新知
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
导入新课
情境引入
探究新知
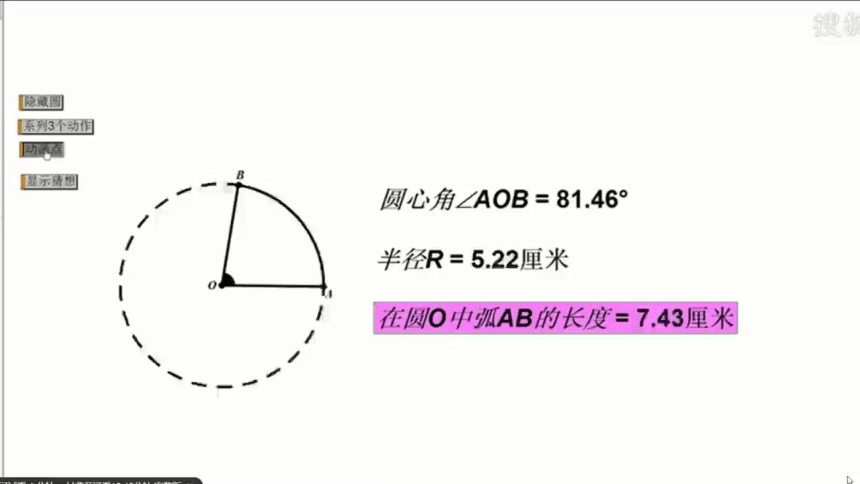
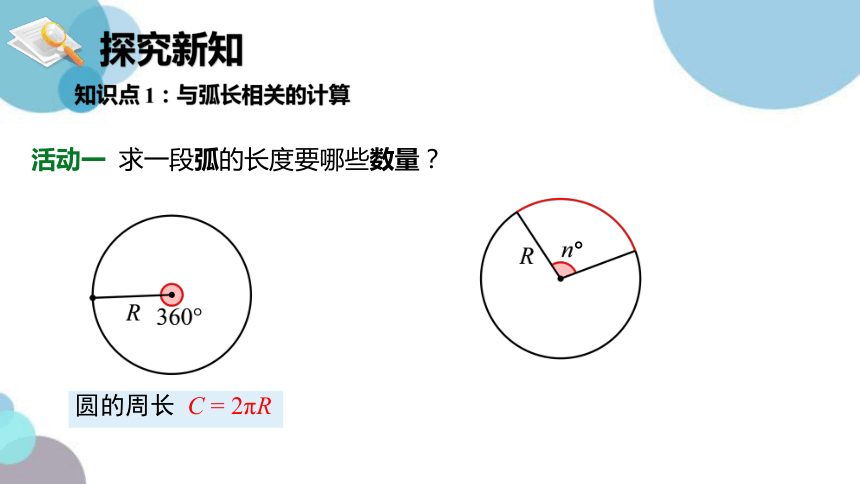
活动一 求一段弧的长度要哪些数量?
°
圆的周长 C = 2πR
知识点 1:与弧长相关的计算
探究新知
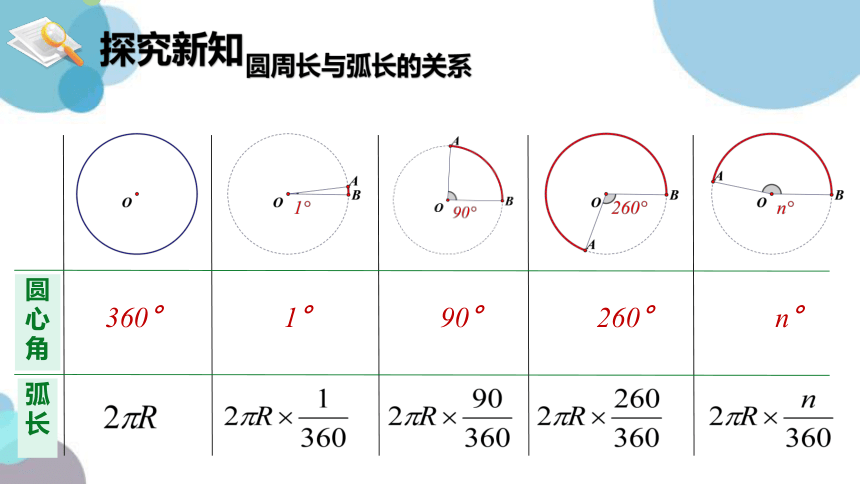
圆周长与弧长的关系
圆心角
弧长
360°
1°
90°
260°
n°
探究新知
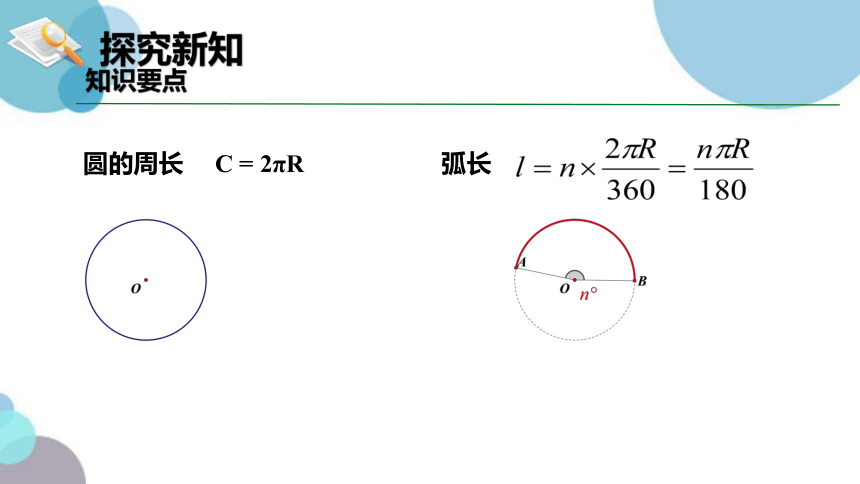
知识要点
圆的周长 C = 2πR
弧长
跟踪练习
算一算(1)已知弧所对的圆心角为60°,半径是4,则弧长为 .
(2)已知弧长为24 cm,弧所在的圆的半径为30cm,则弧所对的圆心角的度数为 .
(3)已知弧所在圆的圆心角为120°,弧长为3 cm,则半径为 .
144°
例题讲解
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L.(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
L=2×700+1570=2970(mm).
答:管道的展直长度为2970mm.
700 mm
700 mm
R = 900 mm
(
100°
A
C
B
D
O
探究新知
扇形:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形. 如图,黄色部分是一个扇形,记作扇形OAB.
概念学习
知识点 :与扇形相关的计算
探究新知
下列图形是扇形吗?
判一判
√
×
×
×
√
探究新知
圆的面积与扇形的面积关系
圆心角
面积
360°
1°
90°
260°
n°
探究新知
知识要点
圆的面积 S = πR2
扇形面积
探究新知
弧长公式和扇形的面积公式之间的关系.
跟踪练习
2.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇= .
3.一个扇形的圆心角为120°,面积为3 ,则这个扇形的半径是 .
4.一个扇形的弧长是20 ,面积是240 ,则扇形的半径为 ,圆心角为 .
1.已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积S扇= .
3cm
24cm
150°
课堂总结
圆的周长
C = 2πR
弧长
圆的面积
S = πR2
扇形面积
1.课后习题24.4;
2.完成练习册本课时的习题。
课后作业
第二十四章 圆
24.4弧长和扇形面积
学习目标
重点
难点
会利用弧长和扇形面积的计算公式进行计算.
探索弧长计算方法和扇形面积计算方法.
(1) 理解弧长和扇形面积公式的探求过程.
(2)会利用弧长和扇形面积的计算公式进行计算.
情境引入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
探究新知
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
导入新课
情境引入
探究新知
活动一 求一段弧的长度要哪些数量?
°
圆的周长 C = 2πR
知识点 1:与弧长相关的计算
探究新知
圆周长与弧长的关系
圆心角
弧长
360°
1°
90°
260°
n°
探究新知
知识要点
圆的周长 C = 2πR
弧长
跟踪练习
算一算(1)已知弧所对的圆心角为60°,半径是4,则弧长为 .
(2)已知弧长为24 cm,弧所在的圆的半径为30cm,则弧所对的圆心角的度数为 .
(3)已知弧所在圆的圆心角为120°,弧长为3 cm,则半径为 .
144°
例题讲解
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L.(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
L=2×700+1570=2970(mm).
答:管道的展直长度为2970mm.
700 mm
700 mm
R = 900 mm
(
100°
A
C
B
D
O
探究新知
扇形:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形. 如图,黄色部分是一个扇形,记作扇形OAB.
概念学习
知识点 :与扇形相关的计算
探究新知
下列图形是扇形吗?
判一判
√
×
×
×
√
探究新知
圆的面积与扇形的面积关系
圆心角
面积
360°
1°
90°
260°
n°
探究新知
知识要点
圆的面积 S = πR2
扇形面积
探究新知
弧长公式和扇形的面积公式之间的关系.
跟踪练习
2.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇= .
3.一个扇形的圆心角为120°,面积为3 ,则这个扇形的半径是 .
4.一个扇形的弧长是20 ,面积是240 ,则扇形的半径为 ,圆心角为 .
1.已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积S扇= .
3cm
24cm
150°
课堂总结
圆的周长
C = 2πR
弧长
圆的面积
S = πR2
扇形面积
1.课后习题24.4;
2.完成练习册本课时的习题。
课后作业
同课章节目录
