初中数学人教版八年级上册 12.2 全等三角形的判定---sss教学设计(表格式)
文档属性
| 名称 | 初中数学人教版八年级上册 12.2 全等三角形的判定---sss教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 173.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-06 00:00:00 | ||
图片预览


文档简介
教学设计
课题 第 2课时 全等三角形的判定---sss
课型 新授课. 复习课□ 试卷讲评课□ 其它课□
教学内容分析本节课是一节新授课,全等三角形的研究,实际是平面几何中对封闭的两个图形关系研究的第一步。全等是两个三角形间最简单、最常见的关系本节课既是前面所学知识的延申与拓展,又是后继学习相似三角形条件的基础,在知识结构上,等腰三角形,直角三角形,线段的垂直平分线,角的平分线的性质等内容都要通过证明两个三角形全等来加以解决,在能力培养上,无论是逻辑思维能力,推理论证还是分析问题解决问题的能力,都可在全等三角形的教学中得以提高。而且证明全等三角形是证明线段相等和角相等的重要手段,本节作为证明两个三角形全等的依据之一,因此成为重中之重。
学情分析学生现在处于几何推理论证的初步阶段,从这章开始,学生应该逐步学会几何证明,几何证明题的推理证明的书写对学生来说难度较大,同时,我们知道,以前学生学习几何都是一些简单的图形,从这章开始出现了几个图形的变换或叠加,学生在解题过程中,找全等条件是一个难点.
学习目标构建三角形全等三角形的探索思路。体会研究几何问题的方法.;探索并理解边边边判定方法,会用边边边判定方法证明三角形全等.:会用尺规做一个角等于已知角,了解作图的道理。重点:构建三角形全等三角形的探索思路,边边边判定方法 难点:探索三角形全等的条件
评价任务达成目标(1)的标志是:学生知道判定三角形全等的含义,为了寻求比三个条件更简捷的判定方法,从“一 个条件”开始,逐渐增加条件的增数量,一次探究“一个条件”,“两个条件”,“三个条件”能否保证两个三角形全等。在探索判定方法的过程中,体会作图、观察、分析、猜想等研究几何问题的方法达成目标(2)的标志是:学生能在教师的引导下做两个三边分别相等的三角形,通过观察、比较、分析,概 括出全等三角形“边边边”判定方法,学生能理解边边边判定方法的含义,会用边边边判定方法进行一些简 单的证明达成目标(3)的标志是:学生能正确使用直尺和圆规作一个角等于已知角,并用“边边边”判定方法解释做法的合理性
教学评活动过程
教师活动 学生活动
环节一:探索三角形全等的条件
学生活动
教师活动 1.学生思考教师提出的问题
我们知道,如果两个三角形全等,那么它们的对应
边相等,对应角相等。反过来根据全等三角形的定
义,反过来根据全等三角形的定义,如果两个三角
形满足三条边分别相等,三个角分别相等这六个条 学生独立思考,然后小组交流并派代表发言.
件,就能判定两个三角形全等
问题 1:是否一定要满足三条边分别相等,三个角分别相等这六个条件才能保证两个三角形全等 在探究过程中,可以通过画图加以说明,也可以利 用三角尺进行说明。
呢?? 学生独立思考,教师适时点拨。学生分三组分别进
追问 1:上述六个条件中,有些条件是相关的,能否在这六个条件中选出部分条件,简捷地判定两个 行探究,通过画图、展示、交流
三角形全等呢?你想从哪儿入手开始研究? 最后得出结论,只满足两个条件的两个三角形不一
追问 2:当满足一个条件时,两个三角形全等吗? 追问 3:当满足两个条件时,两个三角形全等吗? 追问 4:当满足三个条件时,两个三角形全等吗?满足三个条件时,又分为几种情况呢? 定全等学生回答问题并相互补充,发现需要分四种情况进
行研究及三边三角。两角一边,两边一角分别相等
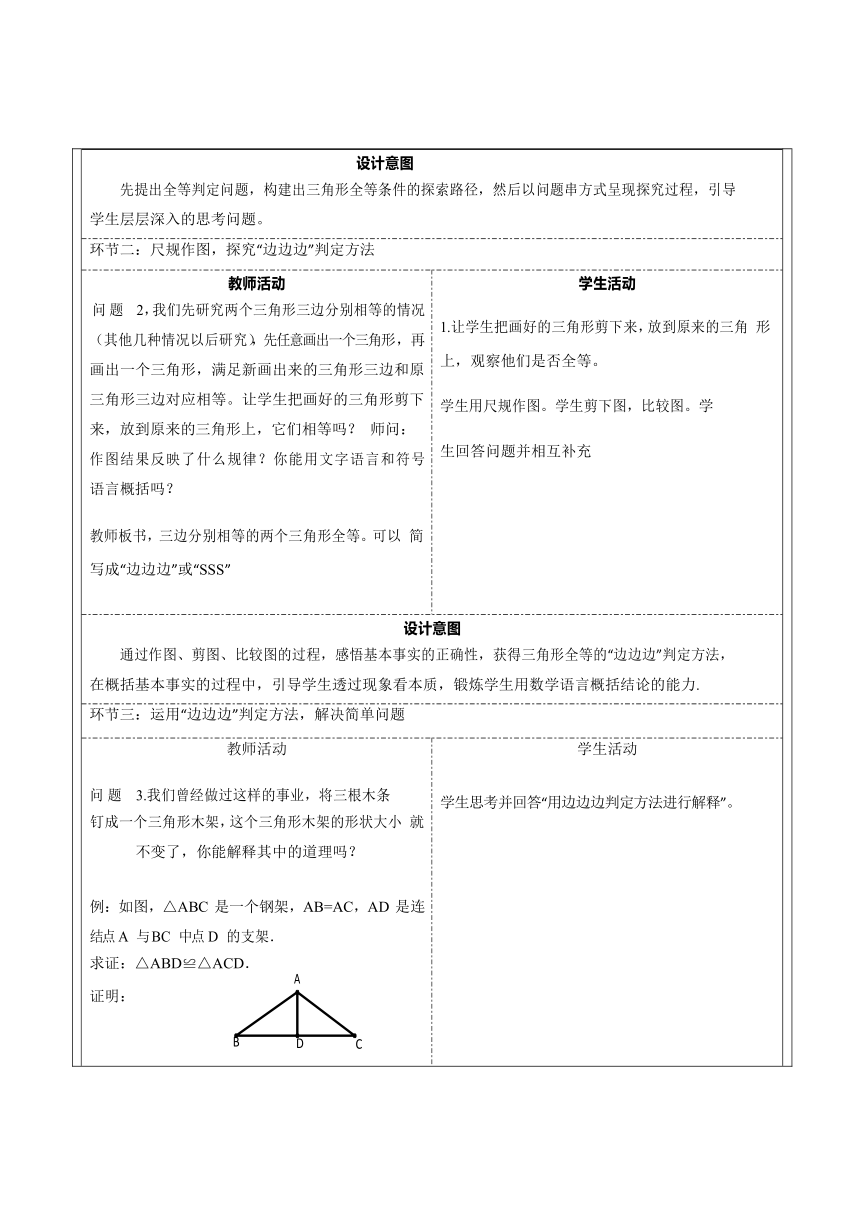
设计意图先提出全等判定问题,构建出三角形全等条件的探索路径,然后以问题串方式呈现探究过程,引导学生层层深入的思考问题。
环节二:尺规作图,探究“边边边”判定方法
教师活动问题 2,我们先研究两个三角形三边分别相等的情况(其他几种情况以后研究),先任意画出一个三角形,再画出一个三角形,满足新画出来的三角形三边和原三角形三边对应相等。让学生把画好的三角形剪下来,放到原来的三角形上,它们相等吗? 师问:作图结果反映了什么规律?你能用文字语言和符号 语言概括吗?教师板书,三边分别相等的两个三角形全等。可以 简写成“边边边”或“SSS” 学生活动1.让学生把画好的三角形剪下来,放到原来的三角 形上,观察他们是否全等。学生用尺规作图。学生剪下图,比较图。学生回答问题并相互补充
设计意图通过作图、剪图、比较图的过程,感悟基本事实的正确性,获得三角形全等的“边边边”判定方法,在概括基本事实的过程中,引导学生透过现象看本质,锻炼学生用数学语言概括结论的能力.
环节三:运用“边边边”判定方法,解决简单问题
教师活动问题 3.我们曾经做过这样的事业,将三根木条钉成一个三角形木架,这个三角形木架的形状大小 就不变了,你能解释其中的道理吗?例:如图,△ABC 是一个钢架,AB=AC,AD 是连结点 A 与 BC 中点 D 的支架.求证:△ABD≌△ACD.A证明:B D C 学生活动学生思考并回答“用边边边判定方法进行解释”。
师生共同分析解题思路。要证明两个三角形形成, 只需看两个三角形三条边是否分别相等,其中有一 个隐含条件是两个三角形公共边.问题 4:你能用直尺和圆规作一个角等于已知角吗?师生分别画出一个任意角∠AOB,教师板书已知和求作的内容,已知:∠AOB. 求作:∠DEF, 使∠DEF=∠AOB 学生口述证明过程,教师板书学生尝试独立作图。如果学生没有思路,教师提示让学生尝试说出作图步骤,学生思考回答做一个角 等于已知角的作图依据是什么
设计意图让学生运用 SSS 条件进行尺规作图,同时体会作图的合理性,增强作图技能
环节四:小结
教师活动教师与学生一起回顾本节课所学的主要内容, 并请学生回答以下问题。本节课学习了哪些主要内容?探索三角形全等的条件,其基本思路是什么?“边边边”判定方法有何作用?
设计意图通过小结,使学生梳理本节课所学内容,掌握本节课的核心——构建三角形全等的条件的探索思路, 以及判定三角形全等的“边边边”方法.
环节五:布置作业
必做题:教科书习题 12.2 第 1,9 题选做题:
如图,已知 B,F,C,D 在同一直线上,AB=EF,AC=ED,
添加一个条件,使得可以有“边边边”判定方法判定△ABC≌△EFD
在(1)的基础上,求证:AB∥EF.
板书设计
三边分别相等的两个三角形全等.简记为“边边边”或“SSS”.
“边边边”判定方法可用几何语言表示为:
作业与拓展学习设计
(1)如图,D、F 是线段 BC 上的两点,AB=EC,AF=ED,BD=CF,求证:△ABF≌△ECD 。
B
A C
已知△ABC,用尺规分别作A1B1C1 与∠A1C1B1,使∠A1B1C1= ∠ABC ,∠A1C1B1=∠ACB.
如图,AD=CB,E、F 是 AC 上两动点,且有 DE=BF.
①若 E、F 运动至图①所示的位置,且有 AF=CE,求证:△ADE≌△CBF.②若 E、F 运动至图②所示的位置,仍有 AF=CE,那么△ADE≌△CBF 还成立吗?为什么?③若 E、F 不重合,AD 和 CB 平行吗?说明理由
特色学习资源分析、技术手段应用说明多媒体希沃白板课件、展台的使用,希沃移动授课手机同步相结合,教师在授课过程中实时录制小组精彩讨论,展台及时将学生的证明过程,习题中出现的共性问题或突出问题进行讲评,反馈及时有效
教学反思与改进本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在找对应线段时感到困难,不能很好应用已知线段加或减公共线段得到对应边相等,还需要在今后的教学中进一步加强巩固和训练.本课在教学时应抓住以下重点:分类问题:教师让学生从实践入手,给定三角形三边,学生在薄纸上画,然后小组的同学看所画三角形是否重合,探索归纳、形成结论.可用多媒体展示现实生活中的实际例子:如桥梁、铁塔、自行车的三角架等,从中体验三角形的稳定性,认识“边边边”可作为三角形全等的判定依据.强调思路分析和书写规范.
课题 第 2课时 全等三角形的判定---sss
课型 新授课. 复习课□ 试卷讲评课□ 其它课□
教学内容分析本节课是一节新授课,全等三角形的研究,实际是平面几何中对封闭的两个图形关系研究的第一步。全等是两个三角形间最简单、最常见的关系本节课既是前面所学知识的延申与拓展,又是后继学习相似三角形条件的基础,在知识结构上,等腰三角形,直角三角形,线段的垂直平分线,角的平分线的性质等内容都要通过证明两个三角形全等来加以解决,在能力培养上,无论是逻辑思维能力,推理论证还是分析问题解决问题的能力,都可在全等三角形的教学中得以提高。而且证明全等三角形是证明线段相等和角相等的重要手段,本节作为证明两个三角形全等的依据之一,因此成为重中之重。
学情分析学生现在处于几何推理论证的初步阶段,从这章开始,学生应该逐步学会几何证明,几何证明题的推理证明的书写对学生来说难度较大,同时,我们知道,以前学生学习几何都是一些简单的图形,从这章开始出现了几个图形的变换或叠加,学生在解题过程中,找全等条件是一个难点.
学习目标构建三角形全等三角形的探索思路。体会研究几何问题的方法.;探索并理解边边边判定方法,会用边边边判定方法证明三角形全等.:会用尺规做一个角等于已知角,了解作图的道理。重点:构建三角形全等三角形的探索思路,边边边判定方法 难点:探索三角形全等的条件
评价任务达成目标(1)的标志是:学生知道判定三角形全等的含义,为了寻求比三个条件更简捷的判定方法,从“一 个条件”开始,逐渐增加条件的增数量,一次探究“一个条件”,“两个条件”,“三个条件”能否保证两个三角形全等。在探索判定方法的过程中,体会作图、观察、分析、猜想等研究几何问题的方法达成目标(2)的标志是:学生能在教师的引导下做两个三边分别相等的三角形,通过观察、比较、分析,概 括出全等三角形“边边边”判定方法,学生能理解边边边判定方法的含义,会用边边边判定方法进行一些简 单的证明达成目标(3)的标志是:学生能正确使用直尺和圆规作一个角等于已知角,并用“边边边”判定方法解释做法的合理性
教学评活动过程
教师活动 学生活动
环节一:探索三角形全等的条件
学生活动
教师活动 1.学生思考教师提出的问题
我们知道,如果两个三角形全等,那么它们的对应
边相等,对应角相等。反过来根据全等三角形的定
义,反过来根据全等三角形的定义,如果两个三角
形满足三条边分别相等,三个角分别相等这六个条 学生独立思考,然后小组交流并派代表发言.
件,就能判定两个三角形全等
问题 1:是否一定要满足三条边分别相等,三个角分别相等这六个条件才能保证两个三角形全等 在探究过程中,可以通过画图加以说明,也可以利 用三角尺进行说明。
呢?? 学生独立思考,教师适时点拨。学生分三组分别进
追问 1:上述六个条件中,有些条件是相关的,能否在这六个条件中选出部分条件,简捷地判定两个 行探究,通过画图、展示、交流
三角形全等呢?你想从哪儿入手开始研究? 最后得出结论,只满足两个条件的两个三角形不一
追问 2:当满足一个条件时,两个三角形全等吗? 追问 3:当满足两个条件时,两个三角形全等吗? 追问 4:当满足三个条件时,两个三角形全等吗?满足三个条件时,又分为几种情况呢? 定全等学生回答问题并相互补充,发现需要分四种情况进
行研究及三边三角。两角一边,两边一角分别相等
设计意图先提出全等判定问题,构建出三角形全等条件的探索路径,然后以问题串方式呈现探究过程,引导学生层层深入的思考问题。
环节二:尺规作图,探究“边边边”判定方法
教师活动问题 2,我们先研究两个三角形三边分别相等的情况(其他几种情况以后研究),先任意画出一个三角形,再画出一个三角形,满足新画出来的三角形三边和原三角形三边对应相等。让学生把画好的三角形剪下来,放到原来的三角形上,它们相等吗? 师问:作图结果反映了什么规律?你能用文字语言和符号 语言概括吗?教师板书,三边分别相等的两个三角形全等。可以 简写成“边边边”或“SSS” 学生活动1.让学生把画好的三角形剪下来,放到原来的三角 形上,观察他们是否全等。学生用尺规作图。学生剪下图,比较图。学生回答问题并相互补充
设计意图通过作图、剪图、比较图的过程,感悟基本事实的正确性,获得三角形全等的“边边边”判定方法,在概括基本事实的过程中,引导学生透过现象看本质,锻炼学生用数学语言概括结论的能力.
环节三:运用“边边边”判定方法,解决简单问题
教师活动问题 3.我们曾经做过这样的事业,将三根木条钉成一个三角形木架,这个三角形木架的形状大小 就不变了,你能解释其中的道理吗?例:如图,△ABC 是一个钢架,AB=AC,AD 是连结点 A 与 BC 中点 D 的支架.求证:△ABD≌△ACD.A证明:B D C 学生活动学生思考并回答“用边边边判定方法进行解释”。
师生共同分析解题思路。要证明两个三角形形成, 只需看两个三角形三条边是否分别相等,其中有一 个隐含条件是两个三角形公共边.问题 4:你能用直尺和圆规作一个角等于已知角吗?师生分别画出一个任意角∠AOB,教师板书已知和求作的内容,已知:∠AOB. 求作:∠DEF, 使∠DEF=∠AOB 学生口述证明过程,教师板书学生尝试独立作图。如果学生没有思路,教师提示让学生尝试说出作图步骤,学生思考回答做一个角 等于已知角的作图依据是什么
设计意图让学生运用 SSS 条件进行尺规作图,同时体会作图的合理性,增强作图技能
环节四:小结
教师活动教师与学生一起回顾本节课所学的主要内容, 并请学生回答以下问题。本节课学习了哪些主要内容?探索三角形全等的条件,其基本思路是什么?“边边边”判定方法有何作用?
设计意图通过小结,使学生梳理本节课所学内容,掌握本节课的核心——构建三角形全等的条件的探索思路, 以及判定三角形全等的“边边边”方法.
环节五:布置作业
必做题:教科书习题 12.2 第 1,9 题选做题:
如图,已知 B,F,C,D 在同一直线上,AB=EF,AC=ED,
添加一个条件,使得可以有“边边边”判定方法判定△ABC≌△EFD
在(1)的基础上,求证:AB∥EF.
板书设计
三边分别相等的两个三角形全等.简记为“边边边”或“SSS”.
“边边边”判定方法可用几何语言表示为:
作业与拓展学习设计
(1)如图,D、F 是线段 BC 上的两点,AB=EC,AF=ED,BD=CF,求证:△ABF≌△ECD 。
B
A C
已知△ABC,用尺规分别作A1B1C1 与∠A1C1B1,使∠A1B1C1= ∠ABC ,∠A1C1B1=∠ACB.
如图,AD=CB,E、F 是 AC 上两动点,且有 DE=BF.
①若 E、F 运动至图①所示的位置,且有 AF=CE,求证:△ADE≌△CBF.②若 E、F 运动至图②所示的位置,仍有 AF=CE,那么△ADE≌△CBF 还成立吗?为什么?③若 E、F 不重合,AD 和 CB 平行吗?说明理由
特色学习资源分析、技术手段应用说明多媒体希沃白板课件、展台的使用,希沃移动授课手机同步相结合,教师在授课过程中实时录制小组精彩讨论,展台及时将学生的证明过程,习题中出现的共性问题或突出问题进行讲评,反馈及时有效
教学反思与改进本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在找对应线段时感到困难,不能很好应用已知线段加或减公共线段得到对应边相等,还需要在今后的教学中进一步加强巩固和训练.本课在教学时应抓住以下重点:分类问题:教师让学生从实践入手,给定三角形三边,学生在薄纸上画,然后小组的同学看所画三角形是否重合,探索归纳、形成结论.可用多媒体展示现实生活中的实际例子:如桥梁、铁塔、自行车的三角架等,从中体验三角形的稳定性,认识“边边边”可作为三角形全等的判定依据.强调思路分析和书写规范.
