24.1旋转 同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版数学九年级下册同步练习24.1旋转
一、单选题
1.如图,将△ABC绕点A逆时针旋转120°,得到△ADE.若点D在线段BC的延长线上,则 的大小为( )
A.30° B.40° C.50° D.60°
2.下列图形是中心对称图形的是( )
A. B.
C. D.
3.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
5.若点 关于原点的对称点是 ,则m+n的值是 ( )
A.1 B.-1 C.3 D.-3
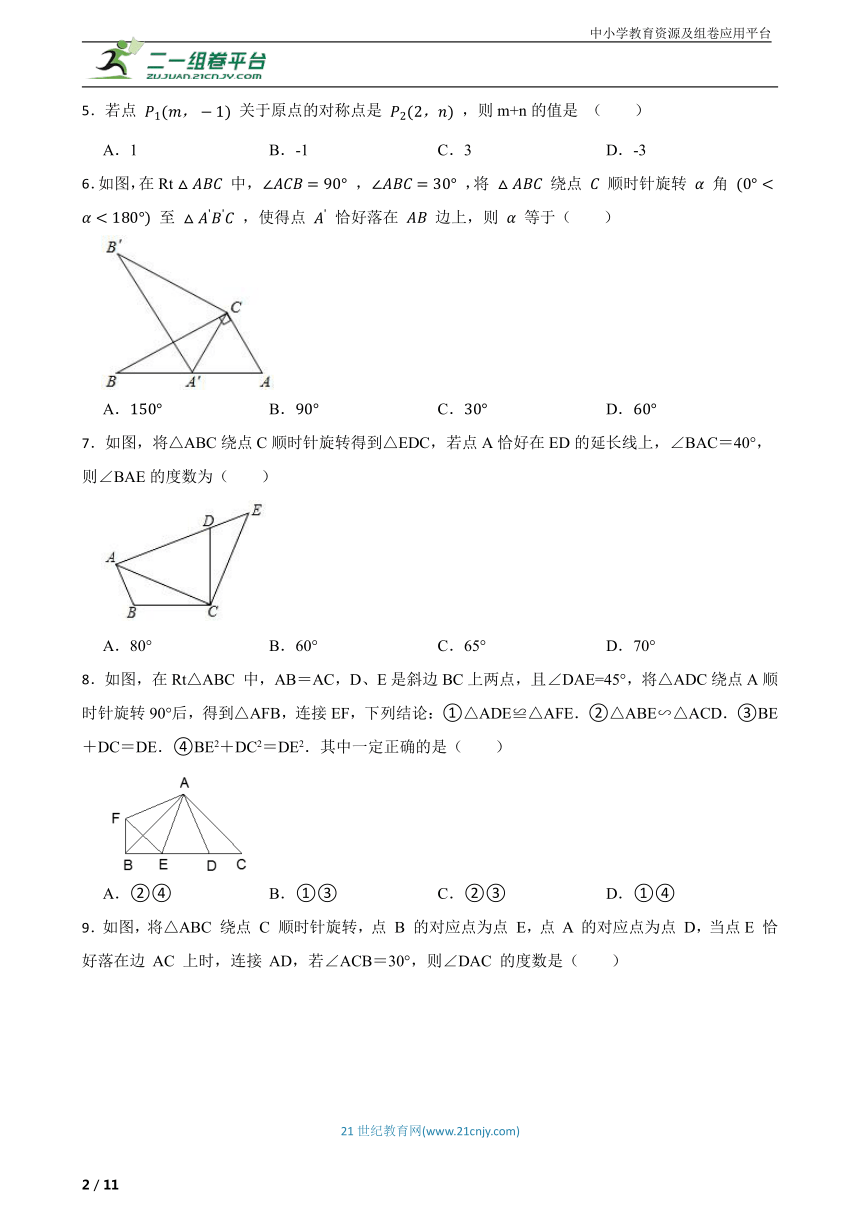
6.如图,在Rt 中, , ,将 绕点 顺时针旋转 角 至 ,使得点 恰好落在 边上,则 等于( )
A. B. C. D.
7.如图,将△ABC绕点C顺时针旋转得到△EDC,若点A恰好在ED的延长线上,∠BAC=40°,则∠BAE的度数为( )
A.80° B.60° C.65° D.70°
8.如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△ADE≌△AFE.②△ABE∽△ACD.③BE+DC=DE.④BE2+DC2=DE2.其中一定正确的是( )
A.②④ B.①③ C.②③ D.①④
9.如图,将△ABC 绕点 C 顺时针旋转,点 B 的对应点为点 E,点 A 的对应点为点 D,当点E 恰好落在边 AC 上时,连接 AD,若∠ACB=30°,则∠DAC 的度数是( )
A.60° B.65° C.70° D.75°
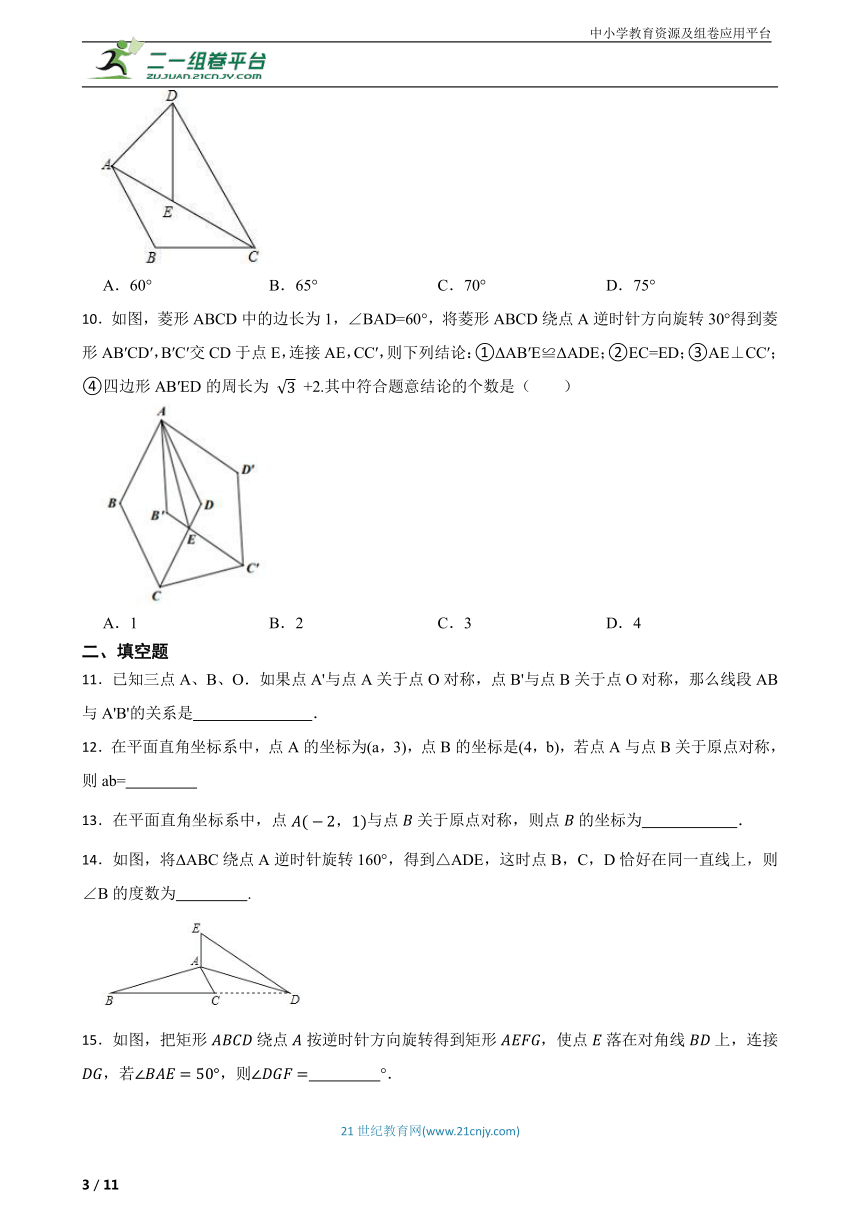
10.如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.已知三点A、B、O.如果点A'与点A关于点O对称,点B'与点B关于点O对称,那么线段AB与A'B'的关系是 .
12.在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点对称,则ab=
13.在平面直角坐标系中,点与点关于原点对称,则点的坐标为 .
14.如图,将ΔABC绕点A逆时针旋转160°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
15.如图,把矩形绕点按逆时针方向旋转得到矩形,使点落在对角线上,连接,若,则 °.
16.如图,在菱形 中, ,将菱形 绕点A逆时针旋转 ,此时点B,C,D的对应点分别为 ,则图中阴影部分的面积为 .
三、计算题
17.图,将绕点A逆时针旋转得到,点和点是对应点,若,求的长.
18.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
19.如图,在平面直角坐标系中,抛物线与轴交于点,点,交轴于点.
(1)求抛物线的解析式;
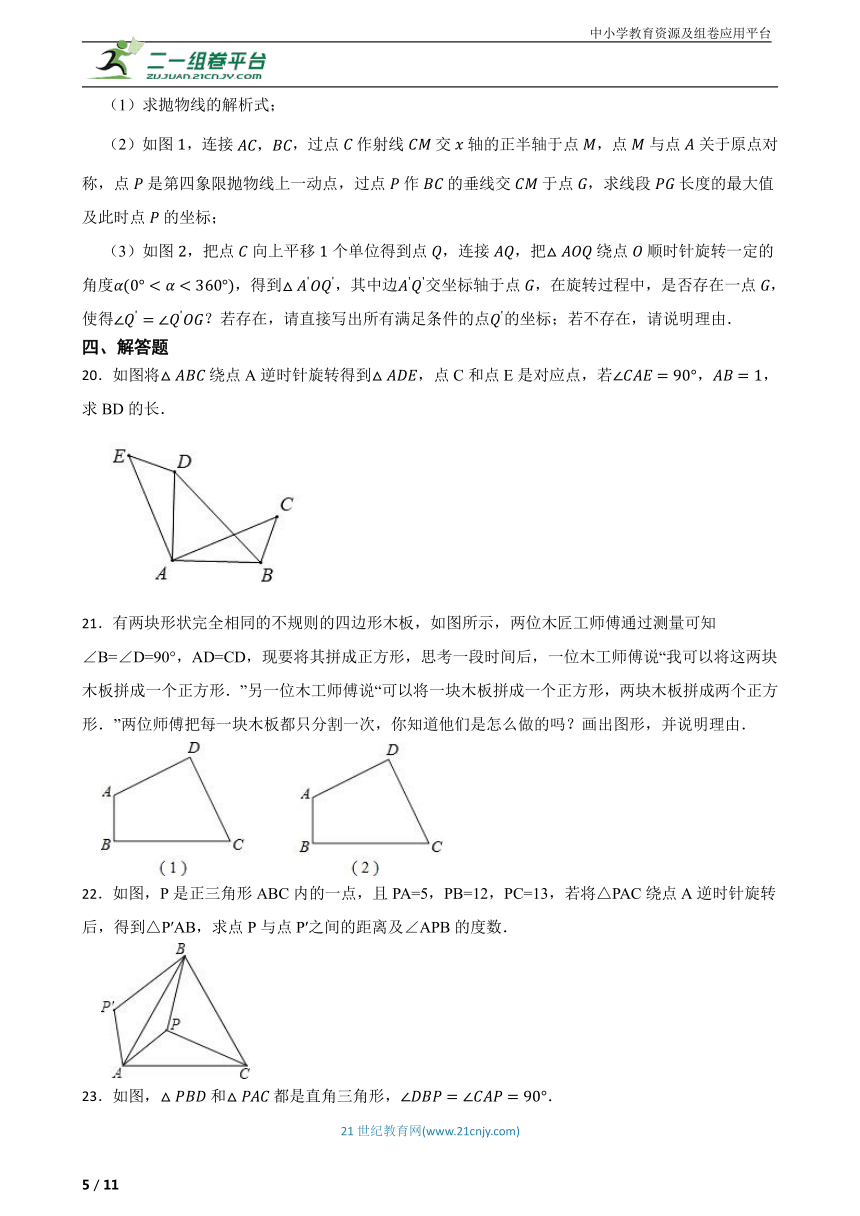
(2)如图,连接,过点作射线交轴的正半轴于点,点与点关于原点对称,点是第四象限抛物线上一动点,过点作的垂线交于点,求线段长度的最大值及此时点的坐标;
(3)如图,把点向上平移个单位得到点,连接,把绕点顺时针旋转一定的角度,得到,其中边交坐标轴于点,在旋转过程中,是否存在一点,使得?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
四、解答题
20.如图将绕点A逆时针旋转得到,点C和点E是对应点,若,,求BD的长.
21.有两块形状完全相同的不规则的四边形木板,如图所示,两位木匠工师傅通过测量可知∠B=∠D=90°,AD=CD,现要将其拼成正方形,思考一段时间后,一位木工师傅说“我可以将这两块木板拼成一个正方形.”另一位木工师傅说“可以将一块木板拼成一个正方形,两块木板拼成两个正方形.”两位师傅把每一块木板都只分割一次,你知道他们是怎么做的吗?画出图形,并说明理由.
22.如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.
23.如图,和都是直角三角形,.
(1)如图1,与直线重合,若,求的度数;
(2)如图2,若保持不动,绕点P逆时针旋转一周.在旋转过程中,当时,求的度数;
(3)如图3,,点E、F分别是线段上一动点,当周长最小时,直接写出的度数(用含的代数式表示).
答案解析部分
1.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
2.【答案】D
【知识点】中心对称及中心对称图形
3.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】B
【知识点】关于原点对称的点的坐标特征
6.【答案】D
【知识点】旋转的性质
7.【答案】A
【知识点】等腰三角形的性质;旋转的性质
8.【答案】D
【知识点】旋转的性质;三角形的综合
9.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
10.【答案】B
【知识点】全等三角形的判定与性质;菱形的性质;旋转的性质
11.【答案】平行且相等
【知识点】中心对称及中心对称图形
12.【答案】12
【知识点】关于原点对称的点的坐标特征
13.【答案】
【知识点】关于原点对称的点的坐标特征
14.【答案】10°
【知识点】旋转的性质
15.【答案】
【知识点】等腰三角形的性质;矩形的性质;旋转的性质
16.【答案】
【知识点】三角形的面积;含30°角的直角三角形;菱形的性质;扇形面积的计算;旋转的性质
17.【答案】
【知识点】勾股定理;旋转的性质
18.【答案】解:依题意:
且
【知识点】关于原点对称的点的坐标特征
19.【答案】(1)抛物线的解析式为;
(2),此时;
(3).
【知识点】待定系数法求二次函数解析式;解直角三角形;旋转的性质
20.【答案】由旋转的性质得:,,
∴.
【知识点】勾股定理;旋转的性质
21.【答案】解:如图(1)所示:将两块四边形拼成正方形,
连接BD,将△DBC绕D点顺时针旋转90度,即可得出△B′BD此时三角形是等腰直角三角形,同理可得出正方形B′EBD.如图(2)将一个四边形拼成正方形,过点D作DE⊥BC于点E,过点D作DF⊥BA交BA的延长线于点F,∴∠FDA+∠ADE=∠CDE+∠ADE=90°,∴∠FDA=∠CDE,在△AFD和△CED中, ,
∴△AFD≌△CED(AAS),∴FD=DE,又∵∠B=∠F=∠BED=90°,∴四边形FBED为正方形.
【知识点】利用旋转设计图案
22.【答案】解:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
答:点P与点P′之间的距离为5,∠APB的度数为150°.
【知识点】勾股定理的逆定理;旋转的性质
23.【答案】(1)解:∵,,
∴,
∴;
(2)解:∵,
∴,
当时,分情况讨论:
①当旋转到如下图所示:
∵,且,
∴,
∴;
②当旋转到如下图所示:
∵,且,
∴,
∴,
∴,
综上,或;
(3)解:作点P关于的对称点,作点P关于的对称点,连接,与交于点E,与交于点F,如图所示:
此时的周长最小,
根据轴对称的性质得,
∴,
同理,,
∵,
∴,
∴,
∴当周长最小时,.
【知识点】平行线的性质;三角形内角和定理;轴对称的应用-最短距离问题;旋转的性质;直角三角形的性质
21世纪教育网(www.21cnjy.com)
2 / 11
沪科版数学九年级下册同步练习24.1旋转
一、单选题
1.如图,将△ABC绕点A逆时针旋转120°,得到△ADE.若点D在线段BC的延长线上,则 的大小为( )
A.30° B.40° C.50° D.60°
2.下列图形是中心对称图形的是( )
A. B.
C. D.
3.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
5.若点 关于原点的对称点是 ,则m+n的值是 ( )
A.1 B.-1 C.3 D.-3
6.如图,在Rt 中, , ,将 绕点 顺时针旋转 角 至 ,使得点 恰好落在 边上,则 等于( )
A. B. C. D.
7.如图,将△ABC绕点C顺时针旋转得到△EDC,若点A恰好在ED的延长线上,∠BAC=40°,则∠BAE的度数为( )
A.80° B.60° C.65° D.70°
8.如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△ADE≌△AFE.②△ABE∽△ACD.③BE+DC=DE.④BE2+DC2=DE2.其中一定正确的是( )
A.②④ B.①③ C.②③ D.①④
9.如图,将△ABC 绕点 C 顺时针旋转,点 B 的对应点为点 E,点 A 的对应点为点 D,当点E 恰好落在边 AC 上时,连接 AD,若∠ACB=30°,则∠DAC 的度数是( )
A.60° B.65° C.70° D.75°
10.如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.已知三点A、B、O.如果点A'与点A关于点O对称,点B'与点B关于点O对称,那么线段AB与A'B'的关系是 .
12.在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点对称,则ab=
13.在平面直角坐标系中,点与点关于原点对称,则点的坐标为 .
14.如图,将ΔABC绕点A逆时针旋转160°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
15.如图,把矩形绕点按逆时针方向旋转得到矩形,使点落在对角线上,连接,若,则 °.
16.如图,在菱形 中, ,将菱形 绕点A逆时针旋转 ,此时点B,C,D的对应点分别为 ,则图中阴影部分的面积为 .
三、计算题
17.图,将绕点A逆时针旋转得到,点和点是对应点,若,求的长.
18.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
19.如图,在平面直角坐标系中,抛物线与轴交于点,点,交轴于点.
(1)求抛物线的解析式;
(2)如图,连接,过点作射线交轴的正半轴于点,点与点关于原点对称,点是第四象限抛物线上一动点,过点作的垂线交于点,求线段长度的最大值及此时点的坐标;
(3)如图,把点向上平移个单位得到点,连接,把绕点顺时针旋转一定的角度,得到,其中边交坐标轴于点,在旋转过程中,是否存在一点,使得?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
四、解答题
20.如图将绕点A逆时针旋转得到,点C和点E是对应点,若,,求BD的长.
21.有两块形状完全相同的不规则的四边形木板,如图所示,两位木匠工师傅通过测量可知∠B=∠D=90°,AD=CD,现要将其拼成正方形,思考一段时间后,一位木工师傅说“我可以将这两块木板拼成一个正方形.”另一位木工师傅说“可以将一块木板拼成一个正方形,两块木板拼成两个正方形.”两位师傅把每一块木板都只分割一次,你知道他们是怎么做的吗?画出图形,并说明理由.
22.如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.
23.如图,和都是直角三角形,.
(1)如图1,与直线重合,若,求的度数;
(2)如图2,若保持不动,绕点P逆时针旋转一周.在旋转过程中,当时,求的度数;
(3)如图3,,点E、F分别是线段上一动点,当周长最小时,直接写出的度数(用含的代数式表示).
答案解析部分
1.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
2.【答案】D
【知识点】中心对称及中心对称图形
3.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】B
【知识点】关于原点对称的点的坐标特征
6.【答案】D
【知识点】旋转的性质
7.【答案】A
【知识点】等腰三角形的性质;旋转的性质
8.【答案】D
【知识点】旋转的性质;三角形的综合
9.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
10.【答案】B
【知识点】全等三角形的判定与性质;菱形的性质;旋转的性质
11.【答案】平行且相等
【知识点】中心对称及中心对称图形
12.【答案】12
【知识点】关于原点对称的点的坐标特征
13.【答案】
【知识点】关于原点对称的点的坐标特征
14.【答案】10°
【知识点】旋转的性质
15.【答案】
【知识点】等腰三角形的性质;矩形的性质;旋转的性质
16.【答案】
【知识点】三角形的面积;含30°角的直角三角形;菱形的性质;扇形面积的计算;旋转的性质
17.【答案】
【知识点】勾股定理;旋转的性质
18.【答案】解:依题意:
且
【知识点】关于原点对称的点的坐标特征
19.【答案】(1)抛物线的解析式为;
(2),此时;
(3).
【知识点】待定系数法求二次函数解析式;解直角三角形;旋转的性质
20.【答案】由旋转的性质得:,,
∴.
【知识点】勾股定理;旋转的性质
21.【答案】解:如图(1)所示:将两块四边形拼成正方形,
连接BD,将△DBC绕D点顺时针旋转90度,即可得出△B′BD此时三角形是等腰直角三角形,同理可得出正方形B′EBD.如图(2)将一个四边形拼成正方形,过点D作DE⊥BC于点E,过点D作DF⊥BA交BA的延长线于点F,∴∠FDA+∠ADE=∠CDE+∠ADE=90°,∴∠FDA=∠CDE,在△AFD和△CED中, ,
∴△AFD≌△CED(AAS),∴FD=DE,又∵∠B=∠F=∠BED=90°,∴四边形FBED为正方形.
【知识点】利用旋转设计图案
22.【答案】解:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
答:点P与点P′之间的距离为5,∠APB的度数为150°.
【知识点】勾股定理的逆定理;旋转的性质
23.【答案】(1)解:∵,,
∴,
∴;
(2)解:∵,
∴,
当时,分情况讨论:
①当旋转到如下图所示:
∵,且,
∴,
∴;
②当旋转到如下图所示:
∵,且,
∴,
∴,
∴,
综上,或;
(3)解:作点P关于的对称点,作点P关于的对称点,连接,与交于点E,与交于点F,如图所示:
此时的周长最小,
根据轴对称的性质得,
∴,
同理,,
∵,
∴,
∴,
∴当周长最小时,.
【知识点】平行线的性质;三角形内角和定理;轴对称的应用-最短距离问题;旋转的性质;直角三角形的性质
21世纪教育网(www.21cnjy.com)
2 / 11
