24.2.2垂径定理 同步练习(含答案)
文档属性
| 名称 | 24.2.2垂径定理 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 304.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.2.2垂径定理
一、填空题
1.如图,⊙O的半径为10,弦AB的长为12,OD⊥AB,交AB于点D,交⊙O于点C,则CD= .
2.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的直径 cm.
3.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=(弦×矢+矢).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径弦时,平分)可以求解,现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为 平方米.
4.如图,的弦,半径交于点,是的中点,且,则的长为 .
5.已知的直径为, ,是的两条弦,,,,则与之间的距离为 cm.
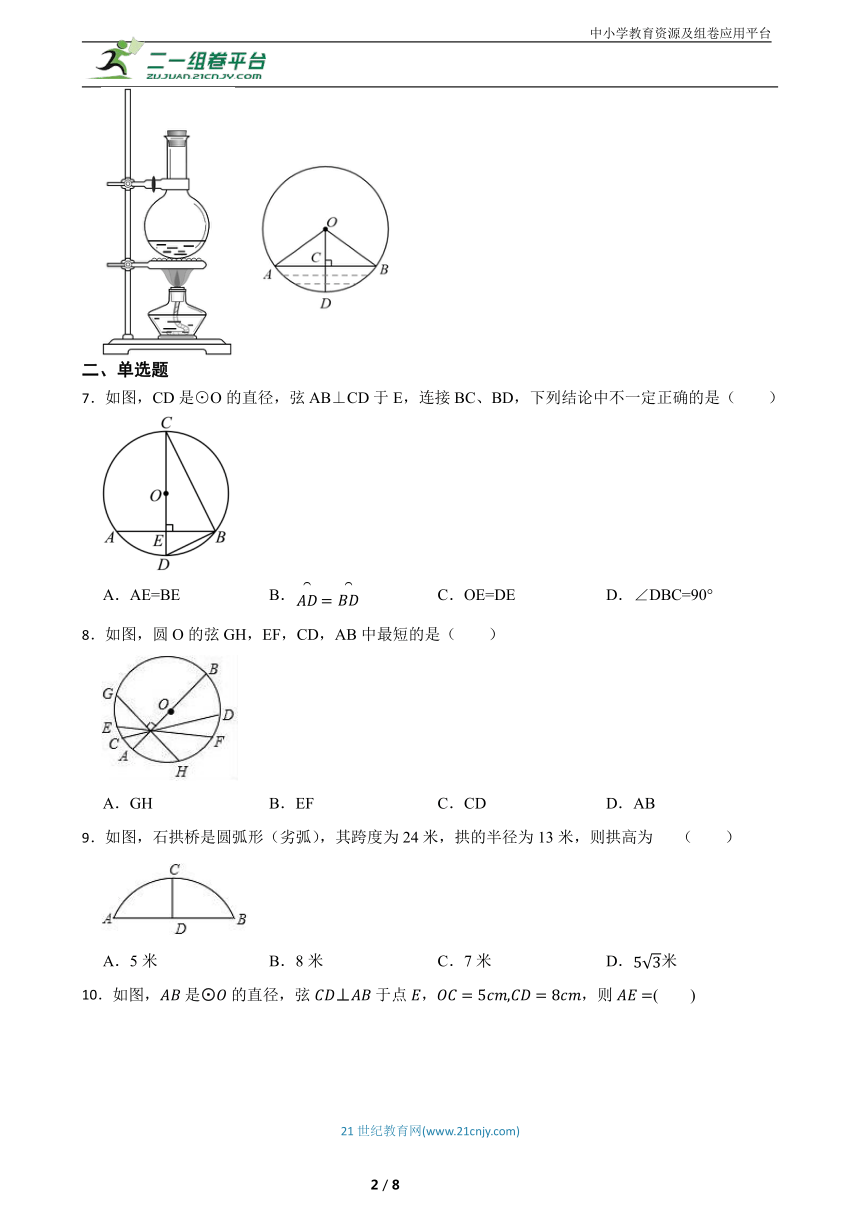
6.如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度,则截面圆中弦的长为 .
二、单选题
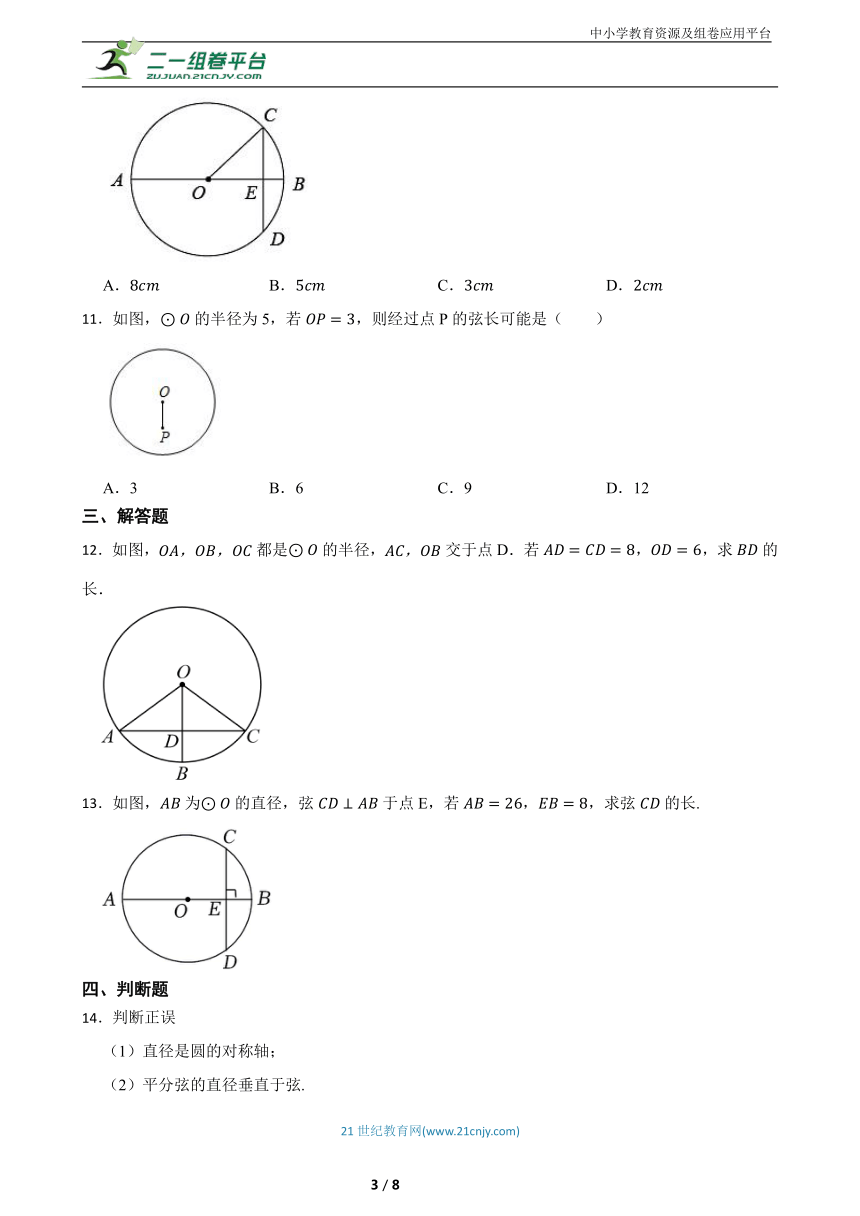
7.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A.AE=BE B. C.OE=DE D.∠DBC=90°
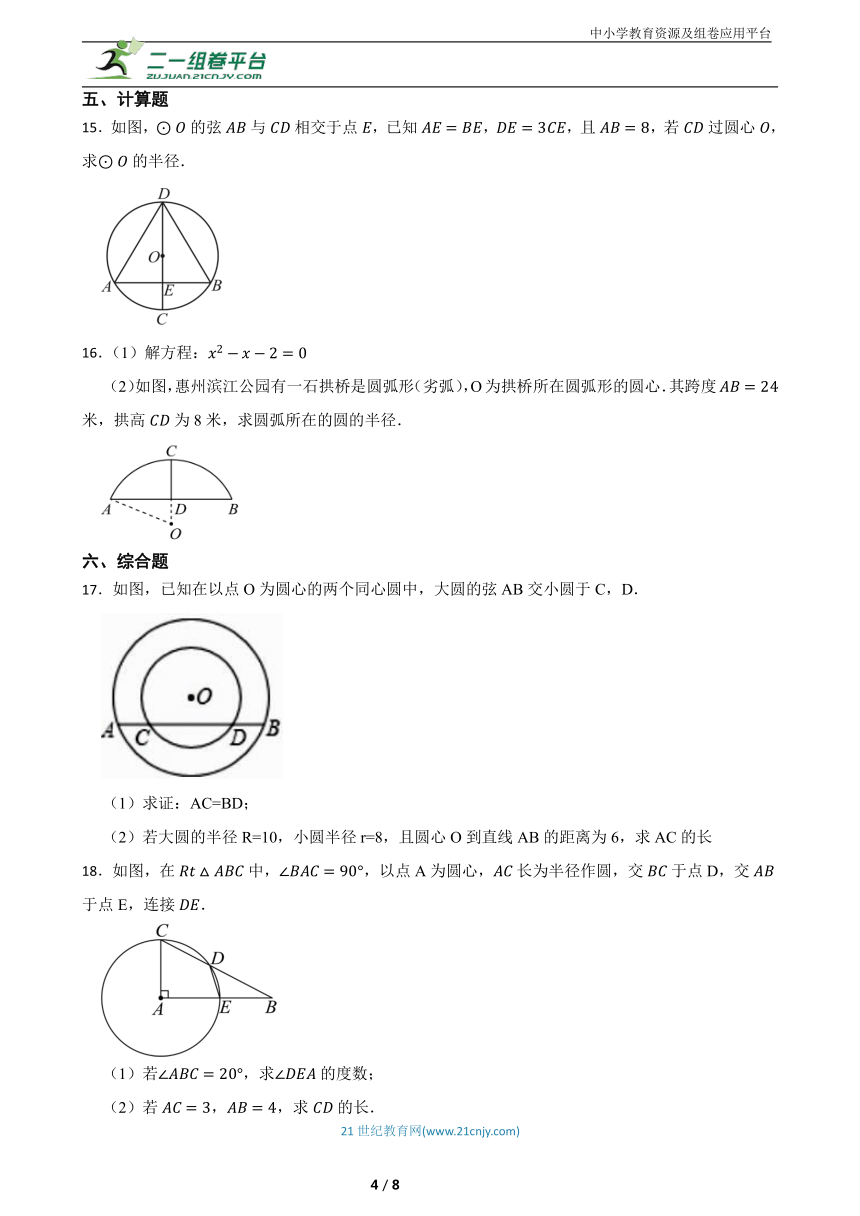
8.如图,圆O的弦GH,EF,CD,AB中最短的是( )
A.GH B.EF C.CD D.AB
9.如图,石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为 ( )
A.5米 B.8米 C.7米 D.米
10.如图,是⊙的直径,弦⊥于点,,则( )
A. B. C. D.
11.如图,的半径为5,若,则经过点P的弦长可能是( )
A.3 B.6 C.9 D.12
三、解答题
12.如图,都是的半径,交于点D.若,,求的长.
13.如图,为的直径,弦于点E,若,,求弦的长.
四、判断题
14.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
五、计算题
15.如图,的弦与相交于点,已知,,且,若过圆心,求的半径.
16.(1)解方程:
(2)如图,惠州滨江公园有一石拱桥是圆弧形(劣弧),O为拱桥所在圆弧形的圆心.其跨度米,拱高为8米,求圆弧所在的圆的半径.
六、综合题
17.如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
18.如图,在中,,以点A为圆心,长为半径作圆,交于点D,交于点E,连接.
(1)若,求的度数;
(2)若,,求的长.
19.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
答案解析部分
1.【答案】2
【知识点】垂径定理
2.【答案】10
【知识点】勾股定理;垂径定理
3.【答案】
【知识点】勾股定理;垂径定理
4.【答案】2
【知识点】垂径定理
5.【答案】2或14
【知识点】垂径定理的实际应用
6.【答案】8
【知识点】勾股定理;垂径定理
7.【答案】C
【知识点】垂径定理
8.【答案】A
【知识点】垂径定理的实际应用
9.【答案】B
【知识点】勾股定理;垂径定理的实际应用
10.【答案】A
【知识点】垂径定理
11.【答案】C
【知识点】勾股定理;垂径定理
12.【答案】4
【知识点】勾股定理;垂径定理
13.【答案】解:连接,如图所示:
∵为的直径,,
∴,,
∴,
在中,由勾股定理得:,
∴.
【知识点】勾股定理;垂径定理
14.【答案】(1)正确
(2)错误
【知识点】垂径定理
15.【答案】的半径为
【知识点】勾股定理;垂径定理
16.【答案】(1),
(2)13米
【知识点】因式分解法解一元二次方程;勾股定理;垂径定理的实际应用
17.【答案】(1)证明:过点O作 OE⊥AB于 E,
∴AE=BE,CE=DE,
∴AE-CE=BE-DE,∴AC=BD
(2)解:由(1)知 OE=6,OA=10,∴AE=8,∵OE=6,OC=8∴ CE =
∴AC=AE-CE=8-2
【知识点】垂径定理
18.【答案】(1)
(2)
【知识点】三角形内角和定理;等腰三角形的性质;勾股定理;垂径定理
19.【答案】(1)解:过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)解:由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD= BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD= OA= ×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD= = =30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即 =300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒
【知识点】勾股定理的应用;垂径定理的实际应用
21世纪教育网(www.21cnjy.com)
1 / 8
24.2.2垂径定理
一、填空题
1.如图,⊙O的半径为10,弦AB的长为12,OD⊥AB,交AB于点D,交⊙O于点C,则CD= .
2.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的直径 cm.
3.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=(弦×矢+矢).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径弦时,平分)可以求解,现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为 平方米.
4.如图,的弦,半径交于点,是的中点,且,则的长为 .
5.已知的直径为, ,是的两条弦,,,,则与之间的距离为 cm.
6.如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度,则截面圆中弦的长为 .
二、单选题
7.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A.AE=BE B. C.OE=DE D.∠DBC=90°
8.如图,圆O的弦GH,EF,CD,AB中最短的是( )
A.GH B.EF C.CD D.AB
9.如图,石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为 ( )
A.5米 B.8米 C.7米 D.米
10.如图,是⊙的直径,弦⊥于点,,则( )
A. B. C. D.
11.如图,的半径为5,若,则经过点P的弦长可能是( )
A.3 B.6 C.9 D.12
三、解答题
12.如图,都是的半径,交于点D.若,,求的长.
13.如图,为的直径,弦于点E,若,,求弦的长.
四、判断题
14.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
五、计算题
15.如图,的弦与相交于点,已知,,且,若过圆心,求的半径.
16.(1)解方程:
(2)如图,惠州滨江公园有一石拱桥是圆弧形(劣弧),O为拱桥所在圆弧形的圆心.其跨度米,拱高为8米,求圆弧所在的圆的半径.
六、综合题
17.如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
18.如图,在中,,以点A为圆心,长为半径作圆,交于点D,交于点E,连接.
(1)若,求的度数;
(2)若,,求的长.
19.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
答案解析部分
1.【答案】2
【知识点】垂径定理
2.【答案】10
【知识点】勾股定理;垂径定理
3.【答案】
【知识点】勾股定理;垂径定理
4.【答案】2
【知识点】垂径定理
5.【答案】2或14
【知识点】垂径定理的实际应用
6.【答案】8
【知识点】勾股定理;垂径定理
7.【答案】C
【知识点】垂径定理
8.【答案】A
【知识点】垂径定理的实际应用
9.【答案】B
【知识点】勾股定理;垂径定理的实际应用
10.【答案】A
【知识点】垂径定理
11.【答案】C
【知识点】勾股定理;垂径定理
12.【答案】4
【知识点】勾股定理;垂径定理
13.【答案】解:连接,如图所示:
∵为的直径,,
∴,,
∴,
在中,由勾股定理得:,
∴.
【知识点】勾股定理;垂径定理
14.【答案】(1)正确
(2)错误
【知识点】垂径定理
15.【答案】的半径为
【知识点】勾股定理;垂径定理
16.【答案】(1),
(2)13米
【知识点】因式分解法解一元二次方程;勾股定理;垂径定理的实际应用
17.【答案】(1)证明:过点O作 OE⊥AB于 E,
∴AE=BE,CE=DE,
∴AE-CE=BE-DE,∴AC=BD
(2)解:由(1)知 OE=6,OA=10,∴AE=8,∵OE=6,OC=8∴ CE =
∴AC=AE-CE=8-2
【知识点】垂径定理
18.【答案】(1)
(2)
【知识点】三角形内角和定理;等腰三角形的性质;勾股定理;垂径定理
19.【答案】(1)解:过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)解:由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD= BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD= OA= ×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD= = =30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即 =300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒
【知识点】勾股定理的应用;垂径定理的实际应用
21世纪教育网(www.21cnjy.com)
1 / 8
