高中数学人教版(2019)第1部分第1节《集合》(含解析)-2025届高考一轮复习-基础摸查 基础夯实 优化提升
文档属性
| 名称 | 高中数学人教版(2019)第1部分第1节《集合》(含解析)-2025届高考一轮复习-基础摸查 基础夯实 优化提升 |  | |
| 格式 | doc | ||
| 文件大小 | 195.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-04 18:29:48 | ||
图片预览




文档简介
第1部分第1节《集合》-2025届高考一轮复习-基础摸查+基础夯实+优化提升
基础摸查
【习题导入】
1.下列集合与集合A={2 022,1}相等的是( )
A.(1,2 022)
B.{(x,y)|x=2 022,y=1}
C.{x|x2-2 023x+2 022=0}
D.{(2 022,1)}
2.已知集合A={-1,1,2,4},B={x||x-1|≤1},则A∩B等于( )
A.{-1,2} B.{1,2} C.{1,4} D.{-1,4}
3.设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2},则A∪B=________, U(A∩B)=________.
【知识归纳】
1.集合与元素
(1)集合中元素的三个特性:____________、____________、____________.
(2)元素与集合的关系是________或________,用符号______或________表示.
(3)集合的表示法:__________、____________、____________.
(4)常见数集的记法
集合 非负整数集(或自然数集) 正整数集 整数集 有理数集 实数集
符号 N*(或N+)
2.集合的基本关系
(1)子集:一般地,对于两个集合A,B,如果集合A中____________都是集合B中的元素,就称集合A为集合B的子集,记作________(或B A).
(2)真子集:如果集合A B,但存在元素x∈B,且________,就称集合A是集合B的真子集,记作________(或B?A).
(3)相等:若A B,且________,则A=B.
(4)空集:不含任何元素的集合叫做空集,记为 .空集是________________的子集,是________________________的真子集.
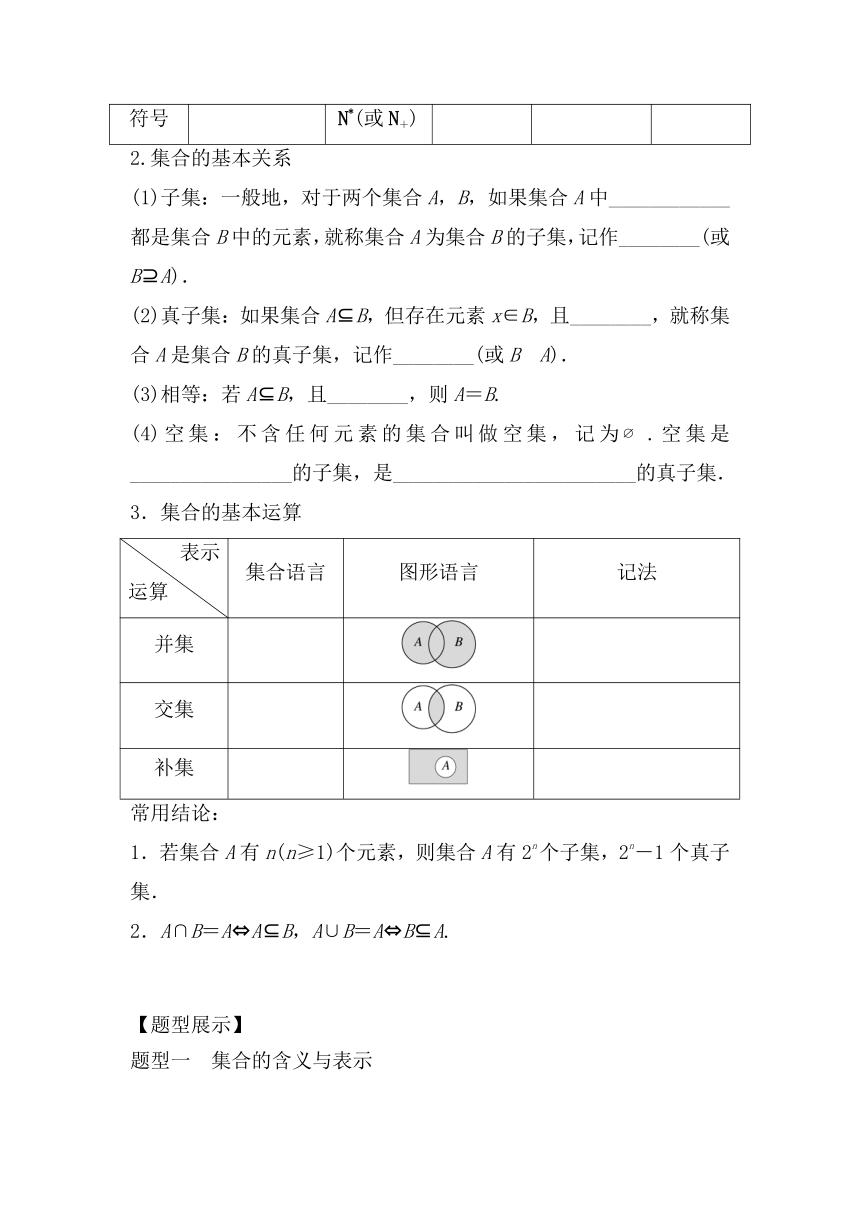
3.集合的基本运算
表示运算 集合语言 图形语言 记法
并集
交集
补集
常用结论:
1.若集合A有n(n≥1)个元素,则集合A有2n个子集,2n-1个真子集.
2.A∩B=A A B,A∪B=A B A.
【题型展示】
题型一 集合的含义与表示
例1 (1)已知集合A={1,a-2,a2-a-1},若-1∈A,则实数a的值为( )
A.1 B.1或0
C.0 D.-1或0
(2)设集合A={(x,y)|y=x},B={(x,y)|y=x2},则集合A∩B的元素个数为( )
A.0 B.1 C.2 D.3
跟踪训练1 (1)已知集合A={0,1,2},B={ab|a∈A,b∈A},则集合B中元素的个数为( )
A.2 B.3 C.4 D.5
(2)(多选)若集合M={x|x-2<0,x∈N},则下列四个命题中,错误的命题是( )
A.0 M B.{0}∈M
C.{1} M D.1 M
题型二 集合间的基本关系
例2 (1)设集合A={x|-1≤x+1≤2},B={x|m-1≤x≤2m+1},当x∈Z时,集合A的真子集有________个;当B A时,实数m的取值范围是________.
(2)已知集合A={x|y=ln(x-2)},B={x|x≥-3},则下列结论正确的是( )
A.A=B B.A∩B=
C.A?B D.B A
跟踪训练2 (1)函数f(x)=的定义域为A,集合B={x|-a≤x≤4-a},若B A,则实数a的取值范围是________________.
(2)(多选)已知非空集合M满足:①M {-2,-1,1,2,3,4},②若x∈M,则x2∈M.则集合M可能是( )
A.{-1,1} B.{-1,1,2,4}
C.{1} D.{1,-2,2}
题型三 集合的基本运算
命题点1 利用集合的运算求参数的值(范围)
例3 已知集合A={x|y=ln(1-x2)},B={x|x≤a},若( RA)∪B=R,则实数a的取值范围为( )
A.(1,+∞) B.[1,+∞)
C.(-∞,1) D.(-∞,1]
命题点2 集合的运算
例4 (1)已知集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T等于( )
A. B.S C.T D.Z
(2)设全集U=R,A={x|-2≤x<4},B={x|y=},则图中阴影部分表示的集合为( )
A.{x|x≤-2} B.{x|x>-2}
C.{x|x≥4} D.{x|x≤4}
跟踪训练3 (1)已知集合A={x|(x-1)·(x-4)<0},B={x|x>a},若A∪B={x|x>1},则a的取值范围是( )
A.[1,4) B.(1,4)
C.[4,+∞) D.(4,+∞)
(2)设全集U={-2,-1,0,1,2,3},集合A={-1,2},B={x|x2-4x+3=0},则 U(A∪B)等于( )
A.{1,3} B.{0,3}
C.{-2,1} D.{-2,0}
题型四 集合的新定义问题
例5 (1)已知集合M={1,2,3,4},A M,集合A中所有元素的乘积称为集合A的“累积值”,且规定:当集合A只有一个元素时,其累积值即为该元素的数值,空集的累积值为0.设集合A的累积值为n.
①若n=3,则这样的集合A共有________个;
②若n为偶数,则这样的集合A共有________个.
(2)(多选)当一个非空数集F满足条件“若a,b∈F,则a+b,a-b,ab∈F,且当b≠0时,∈F”时,称F为一个数域,以下说法正确的是( )
A.0是任何数域的元素
B.若数域F有非零元素,则2 023∈F
C.集合P={x|x=3k,k∈Z}为数域
D.有理数集为数域
跟踪训练4 设集合U={2,3,4},对其子集引进“势”的概念:①空集的“势”最小;②非空子集的元素越多,其“势”越大;③若两个子集的元素个数相同,则子集中最大的元素越大,子集的“势”就越大.最大的元素相同,则第二大的元素越大,子集的“势”就越大,依此类推.若将全部的子集按“势”从小到大的顺序排列,则排在第6位的子集是________.
基础夯实
1.设全集U={1,2,3,4,5},集合M满足 UM={1,3},则( )
A.2∈M B.3∈M
C.4 M D.5 M
2.已知集合A={x|-1A.{x|0≤x<1} B.{x|-1C.{x|13.设集合A={-1,0,1},B={1,3,5},C={0,2,4},则(A∩B)∪C=( )
A.{0} B.{0,1,3,5}
C.{0,1,2,4} D.{0,2,3,4}
4.设集合M={x|x2=x},N={x|lg x≤0},则M∪N等于( )
A.[0,1] B.(0,1]
C.[0,1) D.(-∞,1]
5.已知集合A={x|x2≤1},集合B={x|x∈Z且x+1∈A},则B等于( )
A.{-1,0,1} B.{-2,-1,0}
C.{-2,-1,0,1} D.{-2,-1,0,1,2}
6.已知集合A={x|1m},若A∩( RB)= ,则实数m的取值范围为( )
A.(-∞,1] B.(-∞,1)
C.[1,+∞) D.(1,+∞)
7.已知集合A={1,3,a},B={1,a2-a+1},若B A,则实数a=( )
A.-1 B.2
C.-1或2 D.1或-1或2
8.已知集合A={x|y=log2(x2-8x+15)},B={x|a<x<a+1},若A∩B= ,则实数a的取值范围是( )
A.(-∞,3] B.(-∞,4]
C.(3,4) D.[3,4]
9.设集合A={(x,y)|x+y=1},B={(x,y)|x-y=3},则满足M (A∩B)的集合M的个数是( )
A.0 B.1 C.2 D.3
10.已知集合A={x|x>-1,x∈R},B={x|x2-x-2≥0,x∈R},则下列关系中,正确的是( )
A.A B B. RA RB
C.A∩B= D.A∪B=R
11.若集合A={x∈N|(x-3)(x-2)<6},则A中的元素个数为( )
A.3 B.4 C.5 D.6
12.设集合A={x∈N*|2x<4},B={x∈N|-1A.{x|-1C.{0,1} D.{1}
13.集合M={(x,y)|2x-y=0},N={(x,y)|x+y-3=0},则M∩N等于( )
A.{(2,-1)} B.{2,-1}
C.{(1,2)} D.{1,2}
14.已知集合A={x|x2-6x-7<0},B={y|y=3x,x<1},则A∩( RB)等于( )
A.[3,7) B.(-1,0]∪[3,7)
C.[7,+∞) D.(-∞,-1)∪[7,+∞)
15.(多选)已知集合A={1,3,m2},B={1,m}.若A∪B=A,则实数m的值为( )
A.0 B.1 C.2 D.3
16.(多选)已知全集U的两个非空真子集A,B满足( UA)∪B=B,则下列关系一定正确的是( )
A.A∩B= B.A∩B=B
C.A∪B=U D.( UB)∪A=A
17.已知集合A={x|-5<x<1},B={x|(x-m)(x-2)<0},若A∩B=(-1,n),则m+n=________.
18.已知集合A={1,3,},B={1,m},若B A,则m=________.
19.若全集U=R,A={x|-1≤x≤6},B={x|0<x≤8},则图中阴影部分所表示的集合为________.
20.已知全集U=R,集合M={x∈Z||x-1|<3},N={-4,-2,0,1,5},则Venn图中阴影部分的集合为________.
21.已知集合A={x|x2+x-6=0},B={x|mx+1=0},且A∪B=A,则m的值可能是________.
22.已知集合A={x|(x+3)(x-3)≤0},B={x|2m-3≤x≤m+1}.当m=-1时,则A∪B=________;若A∩B=B,则m的取值范围为________.
23.已知集合A={x|1<x<3},B={x|2m<x<1-m},若A∩B= ,则实数m的取值范围是________.
24.已知集合U={1,2,3,4,5,6},S={1,3,5},T={2,3,6},则S∩( UT)=________,集合S共有________个子集.
优化提升
25.(多选)若集合A={x|sin 2x=1},B=,则下列结论正确的是( )
A.A∪B=B B. RB RA
C.A∩B= D. RA RB
26.(多选)由无理数引发的数学危机一直延续到19世纪,直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2 000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N= ,M中每一个元素小于N中的每一个元素,则称(M,N)为戴德金分割.试判断下列选项中,可能成立的是( )
A.M={x|x<0},N={x|x>0}是一个戴德金分割
B.M没有最大元素,N有一个最小元素
C.M有一个最大元素,N有一个最小元素
D.M没有最大元素,N也没有最小元素
27.(多选)已知全集U={x∈N|log2x<3},A={1,2,3}, U(A∩B)={1,2,4,5,6,7},则集合B可能为( )
A.{2,3,4} B.{3,4,5}
C.{4,5,6} D.{3,5,6}
28.(多选)1872年德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称“戴德金分割”),并把实数理论建立在严格的科学基础上,从而结束了无理数被认为“无理”的时代,也结束了数学史上的第一次大危机.将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N= ,M中的每一个元素都小于N中的每一个元素,则称(M,N)为戴德金分割.试判断下列选项中,可能成立的是( )
A.M={x∈Q|x<0},N={x∈Q|x>0}满足戴德金分割
B.M没有最大元素,N有一个最小元素
C.M有一个最大元素,N有一个最小元素
D.M没有最大元素,N也没有最小元素
29.设A是整数集的一个非空子集,对于k∈A,如果k-1 A且k+1 A,那么k是A的一个“孤立元”,给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的集合共有________个.
30.若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)是集合A的同一种分拆.若集合A有三个元素,则集合A的不同分拆种数是________.
31.某小区连续三天举办公益活动,第一天有190人参加,第二天有130人参加,第三天有180人参加,其中,前两天都参加的有30人,后两天都参加的有40人.第一天参加但第二天没参加活动的有________人,这三天参加活动的最少有________人.
32.我们将b-a称为集合{x|a≤x≤b}的“长度”.若集合M={x|m≤x≤m+2 022},N={x|n-2 023≤x≤n},且M,N都是集合{x|0≤x≤2 024}的子集,则集合M∩N的“长度”的最小值为________.
参考答案:
基础摸查
【习题导入】
1.C 2.B 3.{x|x≥-1} {x|x<2或x≥3}
【知识归纳】
1.(1)确定性 互异性 无序性
(2)属于 不属于 ∈
(3)列举法 描述法 图示法
(4)N Z Q R
2.(1)任意一个元素 A B (2)x A
A?B (3)B A (4)任何集合
任何非空集合
3.{x|x∈A,或x∈B} A∪B
{x|x∈A,且x∈B} A∩B
{x|x∈U,且x A} UA
【题型展示】
例1
(1)C
(2)C
跟踪训练1
(1)C (2)ABD
例2
(1)15 (-∞,-2)∪[-1,0]
(2)C
跟踪训练2
(1)(-∞,-3]∪[5,+∞)
(2)AC
例3 B
例4 (1)C
(2)C
跟踪训练3
(1)A (2)D
例5
(1)2 13
(2)ABD
跟踪训练4
{2,4}
基础夯实
1.A
2.B
3.C
4.A
5.B
6.A
7.C
8.D
9.C
10.D
11.B
12.C
13.C
14.B
15.AD
16.CD
17.0
18.0或3
19.{x|0<x≤6}
20.{-1,2,3}
21.0,-,
22.[-5,3] [0,2]∪(4,+∞)
23.[0,+∞)
24.{1,5} 8
优化提升
25.AB
26.BD
27.BD
28.BD
29.6
30.27
31.160 290
32.2 021
基础摸查
【习题导入】
1.下列集合与集合A={2 022,1}相等的是( )
A.(1,2 022)
B.{(x,y)|x=2 022,y=1}
C.{x|x2-2 023x+2 022=0}
D.{(2 022,1)}
2.已知集合A={-1,1,2,4},B={x||x-1|≤1},则A∩B等于( )
A.{-1,2} B.{1,2} C.{1,4} D.{-1,4}
3.设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2},则A∪B=________, U(A∩B)=________.
【知识归纳】
1.集合与元素
(1)集合中元素的三个特性:____________、____________、____________.
(2)元素与集合的关系是________或________,用符号______或________表示.
(3)集合的表示法:__________、____________、____________.
(4)常见数集的记法
集合 非负整数集(或自然数集) 正整数集 整数集 有理数集 实数集
符号 N*(或N+)
2.集合的基本关系
(1)子集:一般地,对于两个集合A,B,如果集合A中____________都是集合B中的元素,就称集合A为集合B的子集,记作________(或B A).
(2)真子集:如果集合A B,但存在元素x∈B,且________,就称集合A是集合B的真子集,记作________(或B?A).
(3)相等:若A B,且________,则A=B.
(4)空集:不含任何元素的集合叫做空集,记为 .空集是________________的子集,是________________________的真子集.
3.集合的基本运算
表示运算 集合语言 图形语言 记法
并集
交集
补集
常用结论:
1.若集合A有n(n≥1)个元素,则集合A有2n个子集,2n-1个真子集.
2.A∩B=A A B,A∪B=A B A.
【题型展示】
题型一 集合的含义与表示
例1 (1)已知集合A={1,a-2,a2-a-1},若-1∈A,则实数a的值为( )
A.1 B.1或0
C.0 D.-1或0
(2)设集合A={(x,y)|y=x},B={(x,y)|y=x2},则集合A∩B的元素个数为( )
A.0 B.1 C.2 D.3
跟踪训练1 (1)已知集合A={0,1,2},B={ab|a∈A,b∈A},则集合B中元素的个数为( )
A.2 B.3 C.4 D.5
(2)(多选)若集合M={x|x-2<0,x∈N},则下列四个命题中,错误的命题是( )
A.0 M B.{0}∈M
C.{1} M D.1 M
题型二 集合间的基本关系
例2 (1)设集合A={x|-1≤x+1≤2},B={x|m-1≤x≤2m+1},当x∈Z时,集合A的真子集有________个;当B A时,实数m的取值范围是________.
(2)已知集合A={x|y=ln(x-2)},B={x|x≥-3},则下列结论正确的是( )
A.A=B B.A∩B=
C.A?B D.B A
跟踪训练2 (1)函数f(x)=的定义域为A,集合B={x|-a≤x≤4-a},若B A,则实数a的取值范围是________________.
(2)(多选)已知非空集合M满足:①M {-2,-1,1,2,3,4},②若x∈M,则x2∈M.则集合M可能是( )
A.{-1,1} B.{-1,1,2,4}
C.{1} D.{1,-2,2}
题型三 集合的基本运算
命题点1 利用集合的运算求参数的值(范围)
例3 已知集合A={x|y=ln(1-x2)},B={x|x≤a},若( RA)∪B=R,则实数a的取值范围为( )
A.(1,+∞) B.[1,+∞)
C.(-∞,1) D.(-∞,1]
命题点2 集合的运算
例4 (1)已知集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T等于( )
A. B.S C.T D.Z
(2)设全集U=R,A={x|-2≤x<4},B={x|y=},则图中阴影部分表示的集合为( )
A.{x|x≤-2} B.{x|x>-2}
C.{x|x≥4} D.{x|x≤4}
跟踪训练3 (1)已知集合A={x|(x-1)·(x-4)<0},B={x|x>a},若A∪B={x|x>1},则a的取值范围是( )
A.[1,4) B.(1,4)
C.[4,+∞) D.(4,+∞)
(2)设全集U={-2,-1,0,1,2,3},集合A={-1,2},B={x|x2-4x+3=0},则 U(A∪B)等于( )
A.{1,3} B.{0,3}
C.{-2,1} D.{-2,0}
题型四 集合的新定义问题
例5 (1)已知集合M={1,2,3,4},A M,集合A中所有元素的乘积称为集合A的“累积值”,且规定:当集合A只有一个元素时,其累积值即为该元素的数值,空集的累积值为0.设集合A的累积值为n.
①若n=3,则这样的集合A共有________个;
②若n为偶数,则这样的集合A共有________个.
(2)(多选)当一个非空数集F满足条件“若a,b∈F,则a+b,a-b,ab∈F,且当b≠0时,∈F”时,称F为一个数域,以下说法正确的是( )
A.0是任何数域的元素
B.若数域F有非零元素,则2 023∈F
C.集合P={x|x=3k,k∈Z}为数域
D.有理数集为数域
跟踪训练4 设集合U={2,3,4},对其子集引进“势”的概念:①空集的“势”最小;②非空子集的元素越多,其“势”越大;③若两个子集的元素个数相同,则子集中最大的元素越大,子集的“势”就越大.最大的元素相同,则第二大的元素越大,子集的“势”就越大,依此类推.若将全部的子集按“势”从小到大的顺序排列,则排在第6位的子集是________.
基础夯实
1.设全集U={1,2,3,4,5},集合M满足 UM={1,3},则( )
A.2∈M B.3∈M
C.4 M D.5 M
2.已知集合A={x|-1
A.{0} B.{0,1,3,5}
C.{0,1,2,4} D.{0,2,3,4}
4.设集合M={x|x2=x},N={x|lg x≤0},则M∪N等于( )
A.[0,1] B.(0,1]
C.[0,1) D.(-∞,1]
5.已知集合A={x|x2≤1},集合B={x|x∈Z且x+1∈A},则B等于( )
A.{-1,0,1} B.{-2,-1,0}
C.{-2,-1,0,1} D.{-2,-1,0,1,2}
6.已知集合A={x|1
A.(-∞,1] B.(-∞,1)
C.[1,+∞) D.(1,+∞)
7.已知集合A={1,3,a},B={1,a2-a+1},若B A,则实数a=( )
A.-1 B.2
C.-1或2 D.1或-1或2
8.已知集合A={x|y=log2(x2-8x+15)},B={x|a<x<a+1},若A∩B= ,则实数a的取值范围是( )
A.(-∞,3] B.(-∞,4]
C.(3,4) D.[3,4]
9.设集合A={(x,y)|x+y=1},B={(x,y)|x-y=3},则满足M (A∩B)的集合M的个数是( )
A.0 B.1 C.2 D.3
10.已知集合A={x|x>-1,x∈R},B={x|x2-x-2≥0,x∈R},则下列关系中,正确的是( )
A.A B B. RA RB
C.A∩B= D.A∪B=R
11.若集合A={x∈N|(x-3)(x-2)<6},则A中的元素个数为( )
A.3 B.4 C.5 D.6
12.设集合A={x∈N*|2x<4},B={x∈N|-1
13.集合M={(x,y)|2x-y=0},N={(x,y)|x+y-3=0},则M∩N等于( )
A.{(2,-1)} B.{2,-1}
C.{(1,2)} D.{1,2}
14.已知集合A={x|x2-6x-7<0},B={y|y=3x,x<1},则A∩( RB)等于( )
A.[3,7) B.(-1,0]∪[3,7)
C.[7,+∞) D.(-∞,-1)∪[7,+∞)
15.(多选)已知集合A={1,3,m2},B={1,m}.若A∪B=A,则实数m的值为( )
A.0 B.1 C.2 D.3
16.(多选)已知全集U的两个非空真子集A,B满足( UA)∪B=B,则下列关系一定正确的是( )
A.A∩B= B.A∩B=B
C.A∪B=U D.( UB)∪A=A
17.已知集合A={x|-5<x<1},B={x|(x-m)(x-2)<0},若A∩B=(-1,n),则m+n=________.
18.已知集合A={1,3,},B={1,m},若B A,则m=________.
19.若全集U=R,A={x|-1≤x≤6},B={x|0<x≤8},则图中阴影部分所表示的集合为________.
20.已知全集U=R,集合M={x∈Z||x-1|<3},N={-4,-2,0,1,5},则Venn图中阴影部分的集合为________.
21.已知集合A={x|x2+x-6=0},B={x|mx+1=0},且A∪B=A,则m的值可能是________.
22.已知集合A={x|(x+3)(x-3)≤0},B={x|2m-3≤x≤m+1}.当m=-1时,则A∪B=________;若A∩B=B,则m的取值范围为________.
23.已知集合A={x|1<x<3},B={x|2m<x<1-m},若A∩B= ,则实数m的取值范围是________.
24.已知集合U={1,2,3,4,5,6},S={1,3,5},T={2,3,6},则S∩( UT)=________,集合S共有________个子集.
优化提升
25.(多选)若集合A={x|sin 2x=1},B=,则下列结论正确的是( )
A.A∪B=B B. RB RA
C.A∩B= D. RA RB
26.(多选)由无理数引发的数学危机一直延续到19世纪,直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2 000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N= ,M中每一个元素小于N中的每一个元素,则称(M,N)为戴德金分割.试判断下列选项中,可能成立的是( )
A.M={x|x<0},N={x|x>0}是一个戴德金分割
B.M没有最大元素,N有一个最小元素
C.M有一个最大元素,N有一个最小元素
D.M没有最大元素,N也没有最小元素
27.(多选)已知全集U={x∈N|log2x<3},A={1,2,3}, U(A∩B)={1,2,4,5,6,7},则集合B可能为( )
A.{2,3,4} B.{3,4,5}
C.{4,5,6} D.{3,5,6}
28.(多选)1872年德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称“戴德金分割”),并把实数理论建立在严格的科学基础上,从而结束了无理数被认为“无理”的时代,也结束了数学史上的第一次大危机.将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N= ,M中的每一个元素都小于N中的每一个元素,则称(M,N)为戴德金分割.试判断下列选项中,可能成立的是( )
A.M={x∈Q|x<0},N={x∈Q|x>0}满足戴德金分割
B.M没有最大元素,N有一个最小元素
C.M有一个最大元素,N有一个最小元素
D.M没有最大元素,N也没有最小元素
29.设A是整数集的一个非空子集,对于k∈A,如果k-1 A且k+1 A,那么k是A的一个“孤立元”,给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的集合共有________个.
30.若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)是集合A的同一种分拆.若集合A有三个元素,则集合A的不同分拆种数是________.
31.某小区连续三天举办公益活动,第一天有190人参加,第二天有130人参加,第三天有180人参加,其中,前两天都参加的有30人,后两天都参加的有40人.第一天参加但第二天没参加活动的有________人,这三天参加活动的最少有________人.
32.我们将b-a称为集合{x|a≤x≤b}的“长度”.若集合M={x|m≤x≤m+2 022},N={x|n-2 023≤x≤n},且M,N都是集合{x|0≤x≤2 024}的子集,则集合M∩N的“长度”的最小值为________.
参考答案:
基础摸查
【习题导入】
1.C 2.B 3.{x|x≥-1} {x|x<2或x≥3}
【知识归纳】
1.(1)确定性 互异性 无序性
(2)属于 不属于 ∈
(3)列举法 描述法 图示法
(4)N Z Q R
2.(1)任意一个元素 A B (2)x A
A?B (3)B A (4)任何集合
任何非空集合
3.{x|x∈A,或x∈B} A∪B
{x|x∈A,且x∈B} A∩B
{x|x∈U,且x A} UA
【题型展示】
例1
(1)C
(2)C
跟踪训练1
(1)C (2)ABD
例2
(1)15 (-∞,-2)∪[-1,0]
(2)C
跟踪训练2
(1)(-∞,-3]∪[5,+∞)
(2)AC
例3 B
例4 (1)C
(2)C
跟踪训练3
(1)A (2)D
例5
(1)2 13
(2)ABD
跟踪训练4
{2,4}
基础夯实
1.A
2.B
3.C
4.A
5.B
6.A
7.C
8.D
9.C
10.D
11.B
12.C
13.C
14.B
15.AD
16.CD
17.0
18.0或3
19.{x|0<x≤6}
20.{-1,2,3}
21.0,-,
22.[-5,3] [0,2]∪(4,+∞)
23.[0,+∞)
24.{1,5} 8
优化提升
25.AB
26.BD
27.BD
28.BD
29.6
30.27
31.160 290
32.2 021
同课章节目录
