5.3转化 表达 同步课件(共42张PPT)七年级数学上册同步(苏科版2024)
文档属性
| 名称 | 5.3转化 表达 同步课件(共42张PPT)七年级数学上册同步(苏科版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 48.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 21:58:14 | ||
图片预览









文档简介
(共42张PPT)
5.3 转化 表达
第5章 走进几何世界
教学目标
01
认识常见几何体的展开图,并能根据展开图还原对应的几何体
02
能根据图形的变化总结数字有关的规律问题
03
熟悉正方体的11种展开图
几何体的展开与折叠
生活中,人们常常从不同角度去观察一个物体。数学中,我们一般通过平面直观图表示一个空间几何体。
01
课堂引入
我们也可以用平面展开图研究一个空间几何体。
活动——1.画出正方体纸盒(如图)的平面直观图。
02
知识精讲
2.(1)如图,把一个装墨水瓶的长方体纸盒沿某些棱剪开,铺平后得到一个平面展开图,对比展开前后的位置,你知道有条形码的长方形在原长方体纸盒的哪个面吗
02
知识精讲
条形码的长方形在原长方体纸盒的底面。
02
知识精讲
正方体找某一面的对面的口诀:
隔面有面是对面,隔面无面就拐弯。
(2)将无盖圆柱形纸筒的侧面沿虚线展开(如图),得到什么平面图形?
圆柱的侧面展开图是矩形(长方形)
02
知识精讲
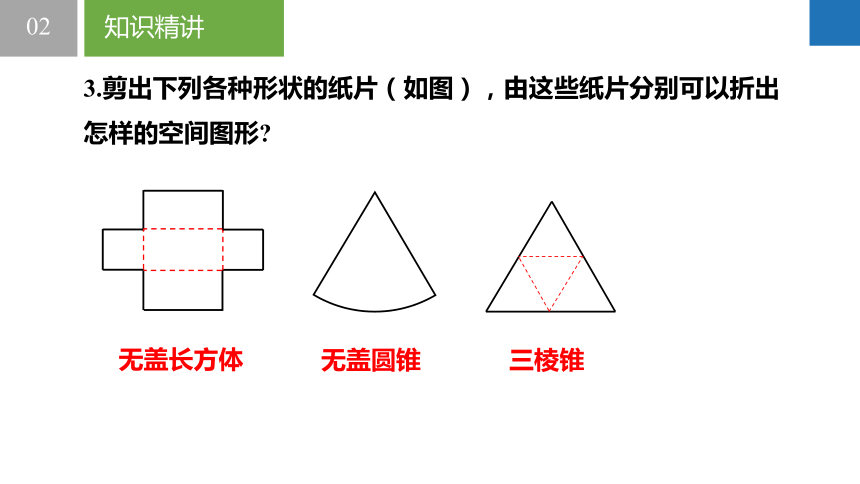
3.剪出下列各种形状的纸片(如图),由这些纸片分别可以折出怎样的空间图形
02
知识精讲
无盖长方体
无盖圆锥
三棱锥
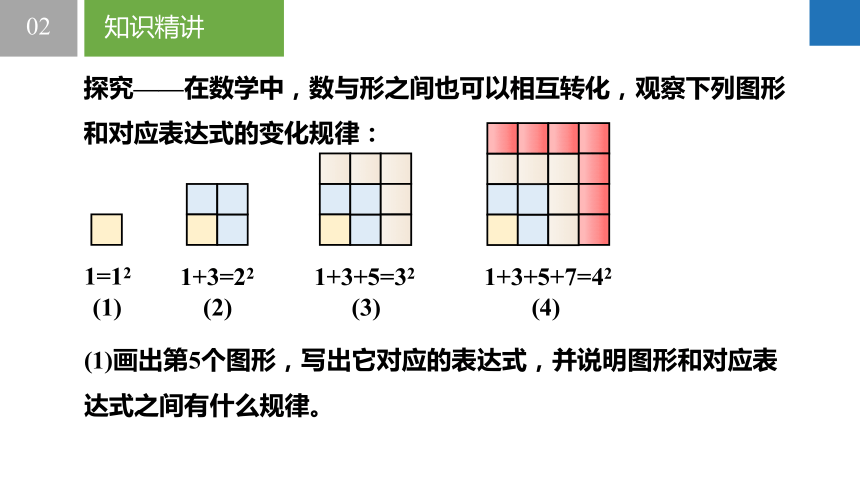
探究——在数学中,数与形之间也可以相互转化,观察下列图形和对应表达式的变化规律:
02
知识精讲
(1)画出第5个图形,写出它对应的表达式,并说明图形和对应表达式之间有什么规律。
1=12
(1) (2) (3) (4)
1+3=22
1+3+5=32
1+3+5+7=42
02
知识精讲
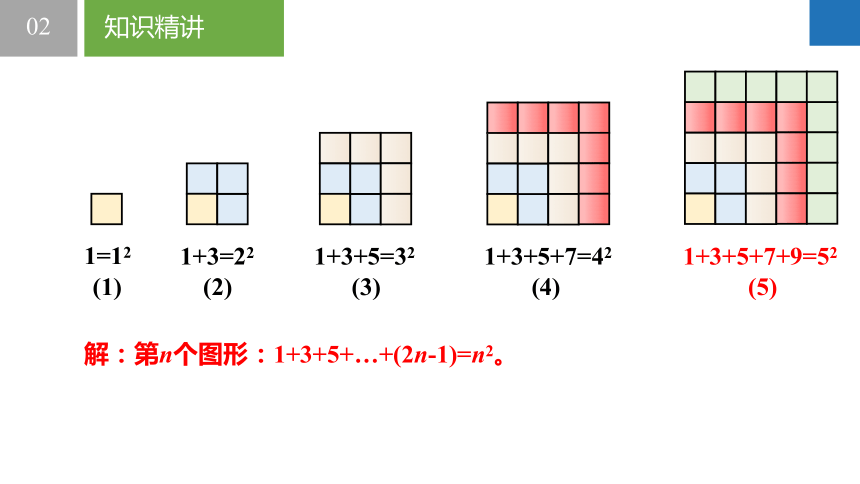
1=12
(1) (2) (3) (4)
1+3=22
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52
(5)
解:第n个图形:1+3+5+…+(2n-1)=n2。
02
知识精讲
(2)利用上面发现的规律计算:
1+3+5+7+9+11+13-15+17+19+21。
第n个图形:1+3+5+…+(2n-1)=n2。
解:1+3+5+7+9+11+13-15+17+19+21
=112
=121。
例1、如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A、C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A. B.
C. D.
B
03
典例精析
例2、一个正方体的表面展开图如图所示,把它折成正方体后,与“山”字相对的字是( )
A.水 B.绿 C.建 D.共
D
03
典例精析
例3-1、下列图形经过折叠可以围成一个棱柱的是( )
A. B. C. D.
D
A. × 底面三角形应该在分布在两侧
B. × 侧面有4个,但底面是三角形
C. × 侧面有3个,但底面是四边形
03
典例精析
例3-2、下列图形,能折叠成圆锥的是( )
A. B. C. D.
圆柱
C
五棱柱
三棱柱
03
典例精析
例4、用同样大小的正方形纸片,按如图方式拼成长方形:
第①个图形中有2张正方形纸片;
第②个图形中有2×(1+2)=6=2×3张正方形纸片;
第③个图形中有2×(1+2+3)=12=3×4张正方形纸片;
第④个图形中有2×(1+2+3+4)=20=4×5张正方形纸片;
…
请你观察上述图形与算式,完成下列问题:
(1)观察可得:1+2+3+…+n=________(用含的代数式表示);
03
典例精析
(1)观察可得:1+2+3+…+n=(用含的代数式表示);
03
典例精析
(2)根据你的发现计算:101+102+103+…+200。
解:101+102+103+…+200
=(1+2+3+…+200)-(1+2+3+…+100)
=-
=20100-5050
=15050。
正方体的展开图
操作:将一个正方体沿某些棱剪开,再展成平面图形。
思考:(1)同一个正方体展开所得到的平面图形有多少种?
(2)在展成平面图形的过程中,一共剪了几条棱
01
课堂引入
沿着红色的7条棱剪开,即可得第1种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第2种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第3种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第4种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第5种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第6种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第7种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第8种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第9种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第10种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第11种平面图形。
01
课堂引入
02
知识精讲
同一个正方体展开所得到的平面图形有11种,在展成平面图形的过程中,一共剪了7条棱。
正方体的展开图
探究1——11种展开图,如何快速记忆呢?
做好分类就行
“一四一”型
02
知识精讲
“二三一”型
“三三”型
“二二二”型
02
知识精讲
02
知识精讲
正方体的展开图
“一四一”型:6个
“二三一”型:3个
“三三”型:1个
“二二二”型:1个
L型
田字型
凹字型
02
知识精讲
正方体的展开图
注意:下列平面图形不是正方体的展开图!
探究2——为什么要剪7条棱,才能得到正方体的展开图呢?
∵正方体共12条棱,
每种展开图内都有5条棱相连,
∴要剪7条棱。
02
知识精讲
例1、下列七个图形中是正方体的平面展开图的有( )
A. 1个 B. 2个 C. 3个 D. 4个
B
“二二二”型,√
×
“一四一”型,√
×
×
×
×
03
典例精析
例2、如图是一个正方体,如图哪个选项是它的展开图( )
A. B. C. D.
B
03
典例精析
例3、如图是一个不完整的正方体平面展开图,需再添上一个面,折叠后才能围成一个正方体.下列添加方式(图中阴影部分)正确的是( )
A. B.
C. D.
D
×
√
×
03
典例精析
×
课后总结
正方体找某一面的对面的口诀:隔面有面是对面,隔面无面就拐弯。
同一个正方体展开所得到的平面图形有11种,在展成平面图形的过程中,一共剪了7条棱。
“一四一”型:6个;“二三一”型:3个;
“三三”型:1个;“二二二”型:1个。 注意:下列平面图形不是正方体的展开图!
5.3 转化 表达
5.3 转化 表达
第5章 走进几何世界
教学目标
01
认识常见几何体的展开图,并能根据展开图还原对应的几何体
02
能根据图形的变化总结数字有关的规律问题
03
熟悉正方体的11种展开图
几何体的展开与折叠
生活中,人们常常从不同角度去观察一个物体。数学中,我们一般通过平面直观图表示一个空间几何体。
01
课堂引入
我们也可以用平面展开图研究一个空间几何体。
活动——1.画出正方体纸盒(如图)的平面直观图。
02
知识精讲
2.(1)如图,把一个装墨水瓶的长方体纸盒沿某些棱剪开,铺平后得到一个平面展开图,对比展开前后的位置,你知道有条形码的长方形在原长方体纸盒的哪个面吗
02
知识精讲
条形码的长方形在原长方体纸盒的底面。
02
知识精讲
正方体找某一面的对面的口诀:
隔面有面是对面,隔面无面就拐弯。
(2)将无盖圆柱形纸筒的侧面沿虚线展开(如图),得到什么平面图形?
圆柱的侧面展开图是矩形(长方形)
02
知识精讲
3.剪出下列各种形状的纸片(如图),由这些纸片分别可以折出怎样的空间图形
02
知识精讲
无盖长方体
无盖圆锥
三棱锥
探究——在数学中,数与形之间也可以相互转化,观察下列图形和对应表达式的变化规律:
02
知识精讲
(1)画出第5个图形,写出它对应的表达式,并说明图形和对应表达式之间有什么规律。
1=12
(1) (2) (3) (4)
1+3=22
1+3+5=32
1+3+5+7=42
02
知识精讲
1=12
(1) (2) (3) (4)
1+3=22
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52
(5)
解:第n个图形:1+3+5+…+(2n-1)=n2。
02
知识精讲
(2)利用上面发现的规律计算:
1+3+5+7+9+11+13-15+17+19+21。
第n个图形:1+3+5+…+(2n-1)=n2。
解:1+3+5+7+9+11+13-15+17+19+21
=112
=121。
例1、如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A、C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A. B.
C. D.
B
03
典例精析
例2、一个正方体的表面展开图如图所示,把它折成正方体后,与“山”字相对的字是( )
A.水 B.绿 C.建 D.共
D
03
典例精析
例3-1、下列图形经过折叠可以围成一个棱柱的是( )
A. B. C. D.
D
A. × 底面三角形应该在分布在两侧
B. × 侧面有4个,但底面是三角形
C. × 侧面有3个,但底面是四边形
03
典例精析
例3-2、下列图形,能折叠成圆锥的是( )
A. B. C. D.
圆柱
C
五棱柱
三棱柱
03
典例精析
例4、用同样大小的正方形纸片,按如图方式拼成长方形:
第①个图形中有2张正方形纸片;
第②个图形中有2×(1+2)=6=2×3张正方形纸片;
第③个图形中有2×(1+2+3)=12=3×4张正方形纸片;
第④个图形中有2×(1+2+3+4)=20=4×5张正方形纸片;
…
请你观察上述图形与算式,完成下列问题:
(1)观察可得:1+2+3+…+n=________(用含的代数式表示);
03
典例精析
(1)观察可得:1+2+3+…+n=(用含的代数式表示);
03
典例精析
(2)根据你的发现计算:101+102+103+…+200。
解:101+102+103+…+200
=(1+2+3+…+200)-(1+2+3+…+100)
=-
=20100-5050
=15050。
正方体的展开图
操作:将一个正方体沿某些棱剪开,再展成平面图形。
思考:(1)同一个正方体展开所得到的平面图形有多少种?
(2)在展成平面图形的过程中,一共剪了几条棱
01
课堂引入
沿着红色的7条棱剪开,即可得第1种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第2种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第3种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第4种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第5种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第6种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第7种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第8种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第9种平面图形。
01
课堂引入
知识精讲
沿着红色的7条棱剪开,即可得第10种平面图形。
01
课堂引入
沿着红色的7条棱剪开,即可得第11种平面图形。
01
课堂引入
02
知识精讲
同一个正方体展开所得到的平面图形有11种,在展成平面图形的过程中,一共剪了7条棱。
正方体的展开图
探究1——11种展开图,如何快速记忆呢?
做好分类就行
“一四一”型
02
知识精讲
“二三一”型
“三三”型
“二二二”型
02
知识精讲
02
知识精讲
正方体的展开图
“一四一”型:6个
“二三一”型:3个
“三三”型:1个
“二二二”型:1个
L型
田字型
凹字型
02
知识精讲
正方体的展开图
注意:下列平面图形不是正方体的展开图!
探究2——为什么要剪7条棱,才能得到正方体的展开图呢?
∵正方体共12条棱,
每种展开图内都有5条棱相连,
∴要剪7条棱。
02
知识精讲
例1、下列七个图形中是正方体的平面展开图的有( )
A. 1个 B. 2个 C. 3个 D. 4个
B
“二二二”型,√
×
“一四一”型,√
×
×
×
×
03
典例精析
例2、如图是一个正方体,如图哪个选项是它的展开图( )
A. B. C. D.
B
03
典例精析
例3、如图是一个不完整的正方体平面展开图,需再添上一个面,折叠后才能围成一个正方体.下列添加方式(图中阴影部分)正确的是( )
A. B.
C. D.
D
×
√
×
03
典例精析
×
课后总结
正方体找某一面的对面的口诀:隔面有面是对面,隔面无面就拐弯。
同一个正方体展开所得到的平面图形有11种,在展成平面图形的过程中,一共剪了7条棱。
“一四一”型:6个;“二三一”型:3个;
“三三”型:1个;“二二二”型:1个。 注意:下列平面图形不是正方体的展开图!
5.3 转化 表达
同课章节目录
