(人教A版数学必修一讲义)第4章第09讲第四章指数函数与对数函数章末题型大总结(8大题型+3大方法)(学生版+解析)
文档属性
| 名称 | (人教A版数学必修一讲义)第4章第09讲第四章指数函数与对数函数章末题型大总结(8大题型+3大方法)(学生版+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-06 00:00:00 | ||
图片预览





文档简介
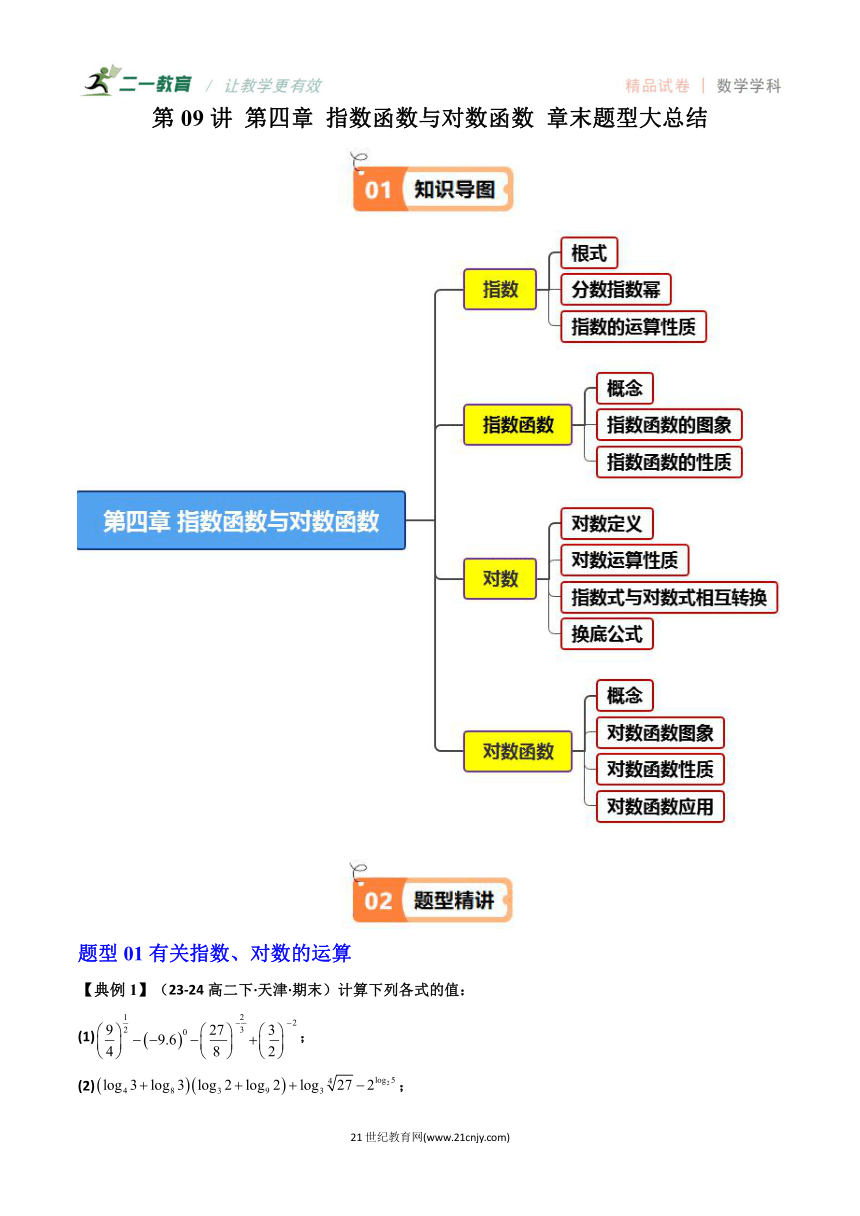
第09讲 第四章 指数函数与对数函数 章末题型大总结
题型01有关指数、对数的运算
【典例1】(23-24高二下·天津·期末)计算下列各式的值:
(1);
(2);
(3)若,,求的值.
【典例2】(24-25高一上·上海·单元测试)计算:
(1);
(2).
【典例3】(2024高三·全国·专题练习)计算下列各式.
(1);
(2)
(3);
(4);
(5);
(6);
(7)已知,求的值.
【变式1】(23-24高二下·宁夏银川·期末)计算
(1)
(2)
【变式2】(24-25高一上·上海·随堂练习)计算下列各式的值:
(1);
(2).
【变式3】(23-24高二下·天津·阶段练习)计算:
(1);
(2).
题型02数的大小比较问题
【典例1】(云南省楚雄彝族自治州2023-2024学年高一下学期期末教育学业质量监测数学试题)已知,则( )
A. B. C. D.
【典例2】(湖南省张家界市2023-2024学年高二下学期期末考试数学试题)已知,,,则( )
A. B.
C. D.
【典例3】(23-24高二下·黑龙江·期末)若,,,则( )
A. B.
C. D.
【变式1】(23-24高二下·北京朝阳·期末)已知,,,则,,的大小关系为( )
A. B. C. D.
【变式2】(2024高三·天津·专题练习)若,,,则,,的大小关系为( )
A. B. C. D.
【变式3】(23-24高二下·北京通州·期末)已知,,,则( )
A. B. C. D.
题型03定义域问题
【典例1】(23-24高一上·安徽·期中)函数的定义域为( )
A. B. C. D.
【典例2】(24-25高一上·上海·课后作业)函数的定义域为 .
【典例3】(24-25高一上·上海·课后作业)已知函数,其定义域为,求的取值范围.
【变式1】(23-24高二下·北京石景山·期末)函数的定义域为 .
【变式2】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2);
(3).
【变式3】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2).
题型04值域问题
【典例1】(21-22高一上·内蒙古赤峰·期中)函数的最大值为 .
【典例2】(2024·上海·模拟预测)函数的最小值为 .
【典例3】(23-24高一上·河南省直辖县级单位·阶段练习)求函数的单调区间与值域.
【变式1】(2024高三·全国·专题练习)已知函数的值域为R,则实数a的取值范围是( )
A. B.
C. D.
【变式2】(24-25高一上·上海·随堂练习)函数的最小值为 .
【变式3】(2024高一上·全国·专题练习)求函数 的值域.
题型05指数(型)函数,对数(型)函数的图象
【典例1】(23-24高一上·云南昆明·期末)如图所示,函数图像①②③④⑤⑥⑦⑧中不属于函数:,的是( )
A.①⑤ B.②⑥
C.③⑦ D.④⑧
【典例2】(24-25高一上·全国·课后作业)当时,在同一平面直角坐标系中,函数与的图象是( ).
A. B.
C. D.
【典例3】(23-24高一下·河北石家庄·开学考试)在同一平面直角坐标系中,函数,(且)的图象可能是( )
A. B.
C. D.
【变式1】(23-24高一上·四川攀枝花·阶段练习)已知且,则函数与在同一直角坐标系中的图象大致是( )
A. B.
C. D.
【变式2】(23-24高一上·内蒙古呼伦贝尔·期末)当时,在同一坐标系中,函数与的图像是( )
A. B.
C. D.
【变式3】(23-24高一上·江西景德镇·期末)已知(且且),则函数与的图象可能是( )
A. B.
C. D.
题型06指数(型)函数,对数(型)函数的性质
【典例1】(2024高三·全国·专题练习)已知函数,若,则实数的取值范围是 .
【典例2】(23-24高一下·安徽阜阳·期末)已知函数为奇函数.
(1)求的值;
(2)若对任意的,关于的不等式恒成立,求正实数的取值范围.
【典例3】(23-24高二下·浙江·期中)已知函数为偶函数.
(1)求的值;
(2)若,判断在的单调性,并用定义法给出证明;
(3)若在区间上恒成立,求的取值范围.
【变式1】(23-24高一下·山西大同·期末)已知函数,,若对于任意,存在,使得,则实数m的取值范围为 .
【变式2】(23-24高二下·天津和平·期末)已知函数(且)是定义在上的奇函数.
(1)求的值;
(2)若,且对于,不等式成立,求实数的取值范围.
【变式3】(23-24高二下·山西吕梁·期末)已知函数,其中.
(1)若,求函数的定义域;
(2)当时,恒成立,求实数的取值范围.
题型07函数与方程
【典例1】(24-25高一上·上海·单元测试)已知函数,若函数恰有一个零点,求实数的取值范围.
【典例2】(23-24高一下·贵州遵义·阶段练习)已知函数.
(1)若在上为增函数,求的取值范围;
(2)若函数在上恰有两个零点,求的取值范围.
【典例3】(23-24高一上·湖南益阳·期末)已知函数,其中,且为奇函数.
(1)求a的值;
(2)若,,,求集合M;
(3)若函数,讨论函数(k为常数)的零点个数.
【变式1】(23-24高一下·安徽滁州·阶段练习)已知函数.
(1)讨论的单调性;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
【变式2】(2024高一·全国·专题练习)已知函数在区间上的最大值为,最小值为.
(1)求实数,的值;
(2)若方程在上有两个不同的实数解,求的取值范围.
【变式3】(2024高二·全国)已知,
(1)若函数与在时有相同的值域,求的取值范围;
(2)若方程在上有两个不同的根,求的取值范围,并证明:.
题型08函数模型及其应用
【典例1】(23-24高一上·浙江丽水·期末)丽水市某革命老区因地制宜发展生态农业,打造“生态特色水果示范区”.该地区某水果树的单株年产量(单位:千克)与单株施肥量(单位:千克)之间的关系为,且单株投入的年平均成本为元.若这种水果的市场售价为元/千克,且水果销路畅通.记该水果树的单株年利润为(单位:元).
(1)求函数的解析式;
(2)求单株施肥量为多少千克时,该水果树的单株年利润最大?最大利润是多少?
【典例2】(23-24高一下·云南昆明·期中)2023年9月17日,联合国教科文组织第45届世界遗产大会通过决议,将中国“普洱景迈山古茶树文化景观”列入《世界遗产名录》,成为全球首个茶主题世界文化遗产.经验表明,某种普洱茶用的水冲泡,等茶水温度降至饮用,口感最佳.某科学兴趣小组为探究在室温条件下,刚泡好的茶水达到最佳饮用口感的放置时间,每隔1分钟测量一次茶水温度,得到茶水温度y(单位:℃)与时间t(单位:分钟)的部分数据如下表所示:
时间t/分钟 0 1 2 3 4 5
水温 95.00 88.00 81.70 76.03 70.93 66.33
(1)给出下列三种函数模型:①,②,③,请根据上表中的数据,选出你认为最符合实际的函数模型,简单叙述理由,并利用表中前3组数据求出相应的解析式;
(2)根据(1)中所求模型,求刚泡好的普洱茶达到最佳饮用口感的放置时间(精确到0.1).(参考数据:)
【典例3】(22-23高一上·河南南阳·期末)某城市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),
每件的销售价格)(单位:元)与时间(单位:天)的函数关系近似满足(为常数,且),日销售量(单位:件)与时间(单位:天)的部分数据如下表所示:
10 15 20 25 30
50 55 60 55 50
已知第10天的日销售收入为505元.
(1)给出以下四个函数模型:①;②;③;④.请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量与时间的变化关系,并求出该函数的解析式;
(2)设该工艺品的日销售收入为(单位:元),求的最小值.
【变式1】(23-24高一下·云南曲靖·期末)某乡镇企业2024年1~4月份生产的产品产量(单位:千件)与收益(单位:万元)的统计数据如下表:
月份
产品产量千件 …
收益万元 …
已知且,给出以下4个函数模型:①;②;③;④.
(1)选择一个恰当的函数模型来描述,之间的关系,并求出其解析式;
(2)已知该乡镇企业由于场地小,最多只能生产500千件,否则需要搬迁,现镇政府想使该企业的收益在10万元以上(含10万元),此企业是否应搬迁?
【变式2】(23-24高一下·湖北·阶段练习)学校为了鼓励学生课余时间积极参加体育锻炼,需要制定一个课余锻炼考核评分制度,建立一个每天得分与当天锻炼时间(单位:分钟,)的函数关系式,要求如下:
(i)函数的图象接近图示;
(ii)每天锻炼时间为0分钟时,当天得分为0分;
(iii)每天锻炼时间为9分钟时,当天得分为6分;
(iiii)每天得分最多不超过12分.
现有以下三个函数模型供选择:
①;②;③.
(1)请根据函数图像性质,结合题设条件,从中选择一个最合适的函数模型并求出解析式;
(2)若学校要求每天的得分不少于9分,求每天至少锻炼多少分钟?
(参考值:)
【变式3】(24-25高一上·全国·课后作业)人们早就发现了放射性物质的衰减现象.在考古工作中,常用的含量来确定有机物的年代.已知放射性物质的衰减服从指数规律:,其中t表示衰减的时间,表示放射性物质的原始质量,表示经衰减了t年后剩余的质量.为计算衰减的年代,通常给出该物质质量衰减一半的时间,称其为该物质的半衰期.的半衰期大约是5730年.人们又知道,放射性物质的衰减速度与其质量成正比.1950年,在伊拉克发现一根古巴比伦王国时期刻有汉谟拉比王朝字样的木炭,当时测定,其的衰减速度为4.09个/(),而新砍伐树木烧成的木炭中的衰减速度为6.68个/().请估算出汉谟拉比王朝所在年代.(参考数据:)
题型09数形结合的思想
【典例1】(23-24高二下·海南·期末)已知函数若关于的方程有两个不同的实根,则实数的取值范围是( )
A. B. C. D.
【典例2】(23-24高二下·浙江杭州·期中)已知函数,若对于正数,直线与函数的图像恰好有个不同的交点,则 .
【典例3】(23-24高二下·山东滨州·期末)设函数 若关于的方程有5个不相等的实数根,则实数的取值范围是 .
【变式1】(2024高三下·全国·专题练习)函数(,且)在上的最大值为13,求实数a的值.
【变式2】(23-24高二下·山东青岛·阶段练习)已知函数.
(1)求函数的解析式;
(2)求函数的单调增区间.
【变式3】(2024高三·全国·专题练习)已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
题型11换元的思想
【典例1】(23-24高一下·云南曲靖·阶段练习)若函数在上是单调函数,且满足对任意,都有,则函数的零点所在的区间为( )
A. B. C. D.
【典例2】(23-24高二下·宁夏银川·期末)已知函数是定义在上的奇函数.
(1)求的解析式并用定义证明的单调性;
(2)使得成立,求实数的取值范围.
【变式1】(24-25高一上·上海·随堂练习)函数的定义域为.
(1)设,求的取值范围;
(2)若恒成立,求的范围.
【变式2】(23-24高三下·北京·阶段练习)已知函数(为实常数).
(1)若函数为奇函数,求的值;
(2)在(1)的条件下,对任意,不等式恒成立,求实数的最大值.
第09讲 第四章 指数函数与对数函数 章末题型大总结
题型01有关指数、对数的运算
【典例1】(23-24高二下·天津·期末)计算下列各式的值:
(1);
(2);
(3)若,,求的值.
【答案】(1)
(2)
(3)1
【分析】(1)根据幂的运算法则计算;
(2)利用换底公式后计算;
(3)指数式与对数式互化后,由对数运算法则、换底公式求解.
【详解】(1)
;
(2)
;
(3),又,
所以.
【典例2】(24-25高一上·上海·单元测试)计算:
(1);
(2).
【答案】(1)
(2)4
【分析】(1)根据二次根式、分数指数幂和对数的运算性质求解;
(2)根据对数的运算性质求解.
【详解】(1)原式
;
(2)原式.
【典例3】(2024高三·全国·专题练习)计算下列各式.
(1);
(2)
(3);
(4);
(5);
(6);
(7)已知,求的值.
【答案】(1)
(2)
(3)4
(4)
(5)
(6)
(7)2
【分析】根据题意,结合指数幂的运算法则和运算性质,逐个计算,即可求解.
【详解】(1)解:由指数幂的运算法则和运算性质,可得:
.
(2)解:由指数幂的运算法则和运算性质,可得:
.
(3)解:由指数幂的运算法则和运算性质,可得:
.
(4)解:由指数幂的运算法则和运算性质,可得:
.
(5)解:由指数幂的运算法则和运算性质,可得:
.
(6)解:由指数幂的运算法则和运算性质,可得:
.
(7)解:因为,所以,所以,
则,
所以.
【变式1】(23-24高二下·宁夏银川·期末)计算
(1)
(2)
【答案】(1)
(2)
【分析】(1)由指数幂的运算性质直接计算即可;
(2)由对数的运算性质直接计算即可.
【详解】(1)
.
(2).
【变式2】(24-25高一上·上海·随堂练习)计算下列各式的值:
(1);
(2).
【答案】(1)2
(2)1
【分析】(1)(2)根据对数运算律计算即可;
【详解】(1)原式
.
(2)原式
.
【变式3】(23-24高二下·天津·阶段练习)计算:
(1);
(2).
【答案】(1)
(2)
【分析】(1)根据指数幂的运算法则计算可得;
(2)根据对数的运算性质及换底公式计算可得.
【详解】(1)
.
(2)
.
题型02数的大小比较问题
【典例1】(云南省楚雄彝族自治州2023-2024学年高一下学期期末教育学业质量监测数学试题)已知,则( )
A. B. C. D.
【答案】A
【分析】根据对数函数和指数函数的单调性比较大小.
【详解】因为在上单调递增,且,
所以,所以,即,
因为在上递增,且,
所以,即,
因为在上单调递减,且,
所以,所以,即,
所以.
故选:A
【典例2】(湖南省张家界市2023-2024学年高二下学期期末考试数学试题)已知,,,则( )
A. B.
C. D.
【答案】D
【分析】根据指对数运算公式及指数函数与对数函数的单调性可比较大小.
【详解】由,
又,且,
所以,
又,
所以,
故选:B.
【典例3】(23-24高二下·黑龙江·期末)若,,,则( )
A. B.
C. D.
【答案】A
【分析】根据对数运算,结合指数函数和对数函数的单调性,转化为和特殊值比较大小,即可判断.,,
【详解】因为,,所以.
故选:A
【变式1】(23-24高二下·北京朝阳·期末)已知,,,则,,的大小关系为( )
A. B. C. D.
【答案】D
【分析】根据对数的运算性质及对数函数的性质计算可得.
【详解】因为,
所以,
所以.
故选:D
【变式2】(2024高三·天津·专题练习)若,,,则,,的大小关系为( )
A. B. C. D.
【答案】D
【分析】因为在上递增,得出,又因在上递增,可得.
【详解】在上递增,且,
所以,所以,即,
因为在上递增,且,
所以,
即,所以,
故选:.
【变式3】(23-24高二下·北京通州·期末)已知,,,则( )
A. B. C. D.
【答案】A
【分析】根据指数函数、对数函数的性质判断即可.
【详解】因为,,
即,,
所以.
故选:A
题型03定义域问题
【典例1】(23-24高一上·安徽·期中)函数的定义域为( )
A. B. C. D.
【答案】A
【分析】根据指数函数的单调性及二次根式的意义可求得原函数的定义域.
【详解】对于函数,有,可得,解得,
因此,函数的定义域为.
故选:A.
【典例2】(24-25高一上·上海·课后作业)函数的定义域为 .
【答案】
【分析】根据具体函数的定义域,结合对数函数的性质列式求解即可.
【详解】函数的定义域需满足不等式,
得或,
所以函数的定义域是.
故答案为:
【典例3】(24-25高一上·上海·课后作业)已知函数,其定义域为,求的取值范围.
【答案】.
【分析】根据对数的性质可得对任意的,都成立,即可利用判别式求解.
【详解】解:∵函数的定义域为,∴,对任意的都成立,
则,解得.
所以的值范围为.
【变式1】(23-24高二下·北京石景山·期末)函数的定义域为 .
【答案】
【分析】根据定义域的求解方法即可.
【详解】要使函数有意义,则,解得,
故答案为: .
【变式2】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2);
(3).
【答案】(1)
(2)
(3)
【分析】(1)(3)根据二次根式与指数函数性质求解;
(2)利用指数函数性质结合分式的定义求解;
【详解】(1)由题意,,,所以定义域为;
(2)由题意,即,所以定义域为;
(3)由题意,即,,,所以定义域为.
【变式3】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2).
【答案】(1)
(2)且.
【分析】(1)根据对数函数真数大于0得到不等式,求出答案;
(2)根据分母不为0和二次根式被开方数非负得到不等式,求出答案.
【详解】(1)要使函数有意义,则,解得,所以函数的定义域为.
(2)由题意知解得且,,
所以函数的定义域为且.
题型04值域问题
【典例1】(21-22高一上·内蒙古赤峰·期中)函数的最大值为 .
【答案】5
【分析】利用换元法,结合指数函数与二次函数的性质即可得解.
【详解】因为,
令,则,,
当,即时,取得最大值5.
故答案为:5.
【典例2】(2024·上海·模拟预测)函数的最小值为 .
【答案】
【分析】根据对数的运算性质将函数化简为,再结合二次函数的性质计算可得.
【详解】因为
,
当,即时,取到最小值,且.
故答案为:
【典例3】(23-24高一上·河南省直辖县级单位·阶段练习)求函数的单调区间与值域.
【答案】单调减区间是,单调增区间是;值域是
【分析】单调性根据复合函数的单调性同增异减得出,值域根据换元法得出.
【详解】函数,
设.
,
当时,,
,即.
函数在上的值域是.
又原函数是由和两个函数复合而成,
第一个函数是单调减函数,第二个函数在区间上是单调增函数,在区间上是单调减函数
函数的单调减区间是,单调增区间是.
【变式1】(2024高三·全国·专题练习)已知函数的值域为R,则实数a的取值范围是( )
A. B.
C. D.
【答案】C
【分析】先求出时,,从而得到当时,的值域包含,得到不等式,求出实数a的取值范围.
【详解】当时,,又的值域为R,
故当时,的值域包含.
故,解得.
故选:C
【变式2】(24-25高一上·上海·随堂练习)函数的最小值为 .
【答案】0
【分析】利用复合函数的性质求函数的最小值,可以考虑使用换元法.
【详解】解:设,则,
的定义域为,
所以函数,在上单调递减,在上单调递增,
由复合函数的同增异减可得:在区间上单调递减,在上单调递增,
,最小值是0.
故答案为:0.
【变式3】(2024高一上·全国·专题练习)求函数 的值域.
【答案】
【分析】根据即可求解.
【详解】,
因为,
所以原函数的值域为.
题型05指数(型)函数,对数(型)函数的图象
【典例1】(23-24高一上·云南昆明·期末)如图所示,函数图像①②③④⑤⑥⑦⑧中不属于函数:,的是( )
A.①⑤ B.②⑥
C.③⑦ D.④⑧
【答案】D
【分析】根据题意,分别由指数函数的图像特点与对数函数的图像特点,即可判断.
【详解】由指数函数的图像性质可知,①②③④为指数函数图像,
且③④为单调递增的指数函数,取可知,③④分别对应,
又①④图像关于轴对称,则①对应,即②不属于;
由对数函数的图像性质可知,⑤⑥⑦⑧为对数函数图像,
其中⑦⑧为单调递减的对数函数,
由“底大图低”可知⑧对应,⑦对应,
且⑤⑧图像关于轴对称,则⑤对应,即⑥不属于;
故选:B
【典例2】(24-25高一上·全国·课后作业)当时,在同一平面直角坐标系中,函数与的图象是( ).
A. B.
C. D.
【答案】A
【分析】由对数函数指数函数单调性以及它们各自所过的定点即可得解.
【详解】当时,函数与分别在各自的定义域内单调递减、单调递增,
故可排除BCD,
且函数与图象分别过定点,经检验,A符合题意.
故选:A.
【典例3】(23-24高一下·河北石家庄·开学考试)在同一平面直角坐标系中,函数,(且)的图象可能是( )
A. B.
C. D.
【答案】D
【分析】分和进行分类讨论判断即可.
【详解】当时,与单调递增,A,B均不符合题意;
当时,与单调递减,
对于,当时,C不正确.
故选:D.
【变式1】(23-24高一上·四川攀枝花·阶段练习)已知且,则函数与在同一直角坐标系中的图象大致是( )
A. B.
C. D.
【答案】C
【分析】由已知结合两函数的单调性及恒过的定点检验各选项即可判断.
【详解】结合与可知,两函数单调性一定相反,排除选项A;
因为恒过定点,恒过定点,排除选项B,D.
故选:C.
【变式2】(23-24高一上·内蒙古呼伦贝尔·期末)当时,在同一坐标系中,函数与的图像是( )
A. B.
C. D.
【答案】D
【分析】根据指数对数函数的图象性质进行判断.
【详解】当时,
函数为单调递减的指数函数,函数为单调递减的对数函数,
观察选项可得D符合.
故选:D.
【变式3】(23-24高一上·江西景德镇·期末)已知(且且),则函数与的图象可能是( )
A. B.
C. D.
【答案】D
【分析】由对数的运算性质可得,讨论的范围,结合指数函数和对数函数的图象的单调性,即可得到答案.
【详解】由,即为,即有;
当时,,
函数在上为增函数,在为增函数,选项B满足;
当时,,
函数在上为减函数,在为减函数,
四个图象均不满足,在同一坐标系中的图象只能是B.
故选:B
题型06指数(型)函数,对数(型)函数的性质
【典例1】(2024高三·全国·专题练习)已知函数,若,则实数的取值范围是 .
【答案】.
【分析】先根据函数的解析式判断得出函数的奇偶性以及单调性.进而将原不等式转化为,即可结合函数的单调性列出不等式,求解即可得出答案.
【详解】由题意知函数定义域为R,且,
所以 为奇函数.
又函数均为R上的增函数,根据复合函数的单调性可知也为R上的增函数,
所以,为R上的函数.
由,得,所以,
解得,
故答案为:.
【典例2】(23-24高一下·安徽阜阳·期末)已知函数为奇函数.
(1)求的值;
(2)若对任意的,关于的不等式恒成立,求正实数的取值范围.
【答案】(1);
(2).
【分析】(1)利用奇函数定义列式计算即得.
(2)由(1)的结论,结合指数函数的性质求出在上的值域,换元分离参数借助函数单调性求解即得.
【详解】(1)由函数为奇函数,
得,解得,
所以.
(2)由(1)知,,当时,,则,因此,
令,,不等式,
等价于,即,而,
因此,,而函数在上单调递减,
即,从而恒成立,则,
所以正实数的取值范围是.
【典例3】(23-24高二下·浙江·期中)已知函数为偶函数.
(1)求的值;
(2)若,判断在的单调性,并用定义法给出证明;
(3)若在区间上恒成立,求的取值范围.
【答案】(1)
(2)单调递增,证明见解析
(3)
【分析】(1)根据,得到方程,求出;
(2)先得到,定义法判断函数单调性步骤,取值,作差,判号,下结论;
(3)参变分离得到,构造,换元后得到,根据单调性求出其最值,得到结论.
【详解】(1)定义域为R,
,
由于函数为偶函数,所以,
即,即,
即恒成立,
.
(2)已知函数,由于函数在上单调递增,
由第(1)问可得,因此
不妨设,,且
则
因为,因此,由因为,,因此,
所以,故,所以函数在单调递增.
(3)由题得在区间上恒成立,即在区间上恒成立,
因为,所以,所以在区间上恒成立,
令,令,
则,
因为在单调递增,
所以函数在上单调递减,故.
.
对任意的恒成立,且,
.
实数的取值范围是.
【变式1】(23-24高一下·山西大同·期末)已知函数,,若对于任意,存在,使得,则实数m的取值范围为 .
【答案】
【分析】根据给定条件,求出函数在上的最大值,探讨函数的性质,并求出在上的最大值,再由已知建立不等式求解即得.
【详解】函数,当时,,
则当,即时,;
函数,显然,
则函数的图象关于直线对称,当时,令,,
,,
由,得,则,,于是,
函数在上单调递增,则函数在上单调递增,
在上单调递减,而在上单调递减,
因此函数在上单调递减,由对称性知,在上单调递增,
则当时,,
由对于任意,存在,使得,得,解得,
所以实数m的取值范围为.
故答案为:
【点睛】结论点睛:函数的定义域为D,,
①存在常数a,b使得,则函数图象关于点对称.
②存在常数a使得,则函数图象关于直线对称.
【变式2】(23-24高二下·天津和平·期末)已知函数(且)是定义在上的奇函数.
(1)求的值;
(2)若,且对于,不等式成立,求实数的取值范围.
【答案】(1)0;
(2).
【分析】(1)由奇函数的性质得,求出值并验证即可.
(2)由,求出的范围并判断的单调性,再脱去法则,参变分离求出函数的最小值即可.
【详解】(1)由是定义在上的奇函数,得,解得,
当时,,,则为上的奇函数,
所以.
(2)由(1)知,由,得,于是,
显然函数是上的单调递增函数,
又是定义在上的奇函数,由,得,
即,因此对,成立,当时,成立,
则对,,
而,当且仅当,即时取等号,从而,
所以实数的取值范围.
【变式3】(23-24高二下·山西吕梁·期末)已知函数,其中.
(1)若,求函数的定义域;
(2)当时,恒成立,求实数的取值范围.
【答案】(1)
(2)
【分析】(1)由真数大于0列出不等式即可求解;
(2)先根据函数为单调递增函数,将转化为,根据题意可转化为在上最小值大于0,然后结合二次函数的性质即可求得.
【详解】(1)当时,,
由得,
故或,
得或,
故函数的定义域为;
(2)由得,
得,
即,
设,
因,故,
所以当时,恒成立,
即为在上最小值大于0,
函数的对称轴为,
当即时,函数在上单调递增,
此时,得,
即满足题意;
当,即时,函数在对称轴取得最小值,
此时,得,
即满足题意;
故的取值范围为.
题型07函数与方程
【典例1】(24-25高一上·上海·单元测试)已知函数,若函数恰有一个零点,求实数的取值范围.
【答案】或
【分析】作出的函数图象,根据图象判断的值.
【详解】解:令得,作出的函数图像如图所示.
由图像可知当或时,只有一解,
此时恰有一个零点.
【典例2】(23-24高一下·贵州遵义·阶段练习)已知函数.
(1)若在上为增函数,求的取值范围;
(2)若函数在上恰有两个零点,求的取值范围.
【答案】(1);
(2).
【分析】(1)根据已知,利用复合函数的单调性和对数函数的定义域及二次函数的单调性,列式即可求出a的取值范围.
(2)利用函数零点的意义,结合对数运算,把问题转化为一元二次方程的实根分布求解.
【详解】(1)令,显然函数在上单调递增,
函数在及右侧区间上单调递增,
而在上为增函数,则,解得,
所以的取值范围是.
(2)由,得,
由函数在上恰有两个零点,得在上有两个不等实根,
于是,解得,
所以的取值范围是.
【典例3】(23-24高一上·湖南益阳·期末)已知函数,其中,且为奇函数.
(1)求a的值;
(2)若,,,求集合M;
(3)若函数,讨论函数(k为常数)的零点个数.
【答案】(1)1
(2)
(3)答案见解析
【分析】(1)根据函数奇偶性定义列出方程求解并检验即得;
(2)先由函数的单调性和奇偶性推导函数的单调性和奇偶性,利用函数奇偶性化简为,利用单调性求得的范围即得.
(3)依题求出,由化简得,就分成和两种情况,讨论方程的解的情况即得.
【详解】(1)因为函数为奇函数,
,
,解得.又,.
经检验,符合题意.
(2)由(1)得,则,
由,因函数为奇函数,
,即为奇函数.
又,
因在上单调递减且为正数,又在定义域内为增函数,
则在上单调递减,故在上单调递减;
由.
,解得:.故集合.
(3),且,
,且,
令.
①当时,有,
.
由得,即.
当时,方程在无实数解.
当时,由得,由,解得.
即当时,,而当时,.
所以,当或或时,函数在只有一个零点.
当且时,函数在有两个零点:和.
②当时,有,.
当时,函数在没有零点.
当时,,由得或.
所以,当或时,函数在有一个零点;
当时,函数在没有零点.
综上所述,当时,函数有且只有一个零点;
当时,函数有两个零点.
【点睛】方法点睛:本题主要考查利用函数的性质求解不等式和判断函数的零点情况,属于难题.
对于抽象不等式的解法,一般从判断函数的奇偶性和单调性入手,将不等式等价变换,将其化成具体不等式组求解;对于含参函数的零点个数问题,一般是将其转化成方程的解的个数或者两函数的图象交点个数解决.
【变式1】(23-24高一下·安徽滁州·阶段练习)已知函数.
(1)讨论的单调性;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
【答案】(1)在和上单调递增,在上单调递减.
(2)
【分析】(1)直接对两段分别研究单调性即可;
(2)画出函数的图象与直线的图象,由数形结合即可求解.
【详解】(1)当时,由单调递增,知在上单调递增;
当时,有,所以在上单调递增;
当时,是二次函数,最小值点是,故在上单调递减,在上单调递增.
综上,在和上单调递增,在上单调递减.
(2)在同一平面直角坐标系中画出函数的图象与直线的图象,如图所示,
由图可知若关于的方程有三个不同的实根,
当且仅当的取值范围是.
【变式2】(2024高一·全国·专题练习)已知函数在区间上的最大值为,最小值为.
(1)求实数,的值;
(2)若方程在上有两个不同的实数解,求的取值范围.
【答案】(1),
(2)
【分析】(1)令,得到,再利用二次函数的性质及条件,即可求出结果;
(2)由(1)及条件得到,令,分离常量得到,再利用函数的单调性,即可求出结果.
【详解】(1)设,则,
因为,对称轴为,所以当,①,
当,②,由①②解得,.
(2)由(1)知,所以,
即,设,得到,即,
又函数在单调递减,在上单调递增,
当时,,又当时,,当时,,
所以要使方程有两个不同的实数解,则.
【变式3】(2024高二·全国)已知,
(1)若函数与在时有相同的值域,求的取值范围;
(2)若方程在上有两个不同的根,求的取值范围,并证明:.
【答案】(1)
(2),证明见解析
【分析】(1)由题意知,求得的取值范围;
(2)令,经判断,可得, ,可得的范围. 消去得证得.
【详解】(1)当时,函数的图象是开口向上,
且对称轴为的抛物线,的值域为,
所以的值域也为的充要条件是,
即,或,
即的取值范围为.
(2),即,
由分析知,不妨设,
令
因为在上是单调函数,
所以在上至多有一个解.
若,即就是的解,
所以,与题设矛盾.因此,
由得,所以,
由得,所以,
综上,当时,方程在上有两个解,
由和,消去得,
由,得.
题型08函数模型及其应用
【典例1】(23-24高一上·浙江丽水·期末)丽水市某革命老区因地制宜发展生态农业,打造“生态特色水果示范区”.该地区某水果树的单株年产量(单位:千克)与单株施肥量(单位:千克)之间的关系为,且单株投入的年平均成本为元.若这种水果的市场售价为元/千克,且水果销路畅通.记该水果树的单株年利润为(单位:元).
(1)求函数的解析式;
(2)求单株施肥量为多少千克时,该水果树的单株年利润最大?最大利润是多少?
【答案】(1)
(2)施肥量为时,单株年利润最大为390元
【分析】(1)由利润=单株产量售价成本,结合分段函数即可求解;
(2)结合二次函数和基本不等式性质分别求出和时对应的,即可得解.
【详解】(1)当时,,
当时,,
故;
(2)当时,的对称轴为,最大值为,
当时,,
当且仅当时,等号成立,
综上施肥量为时,单株年利润最大为390元.
【典例2】(23-24高一下·云南昆明·期中)2023年9月17日,联合国教科文组织第45届世界遗产大会通过决议,将中国“普洱景迈山古茶树文化景观”列入《世界遗产名录》,成为全球首个茶主题世界文化遗产.经验表明,某种普洱茶用的水冲泡,等茶水温度降至饮用,口感最佳.某科学兴趣小组为探究在室温条件下,刚泡好的茶水达到最佳饮用口感的放置时间,每隔1分钟测量一次茶水温度,得到茶水温度y(单位:℃)与时间t(单位:分钟)的部分数据如下表所示:
时间t/分钟 0 1 2 3 4 5
水温 95.00 88.00 81.70 76.03 70.93 66.33
(1)给出下列三种函数模型:①,②,③,请根据上表中的数据,选出你认为最符合实际的函数模型,简单叙述理由,并利用表中前3组数据求出相应的解析式;
(2)根据(1)中所求模型,求刚泡好的普洱茶达到最佳饮用口感的放置时间(精确到0.1).(参考数据:)
【答案】(1)选模型②,理由见解析,解析式为
(2).
【分析】(1)由表格数据可知,函数单调递减且递减速度逐渐变慢,故模型①③不符合,选模型②,把前3组数据代入求出,,的值,即可得到函数解析式;
(2)令,结合对数的运算性质求出的值即可.
【详解】(1)由表格数据可知,函数单调递减且递减速度逐渐变慢,
模型③为单调递增的函数,不符合,
模型①为直线型,不符合递减速度逐渐变慢,
故模型①③不符合,选模型②,
则,解得,
所以;
(2)令,则,
所以,
即刚泡好的普洱茶达到最佳饮用口感的放置时间为.
【典例3】(22-23高一上·河南南阳·期末)某城市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),
每件的销售价格)(单位:元)与时间(单位:天)的函数关系近似满足(为常数,且),日销售量(单位:件)与时间(单位:天)的部分数据如下表所示:
10 15 20 25 30
50 55 60 55 50
已知第10天的日销售收入为505元.
(1)给出以下四个函数模型:①;②;③;④.请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量与时间的变化关系,并求出该函数的解析式;
(2)设该工艺品的日销售收入为(单位:元),求的最小值.
【答案】(1)选②,
(2)
【分析】(1)由第10天的日销售收入为505元,求出,再根据表中数据可知时间变换时,先增后减,则选模型②,再利用待定系数法求出参数,即可得解;
(2)分和,两种情况讨论,结合基本不等式和函数的单调性即可得出答案.
【详解】(1)因为第10天的日销售收入为505元,
则,解得,
由表格中的数据知,当时间变换时,先增后减,
函数模型:①;③;④都是单调函数,
所以选择模型②:,
由,可得,解得,
由,解得,
所以日销售量与时间的变化的关系式为;
(2)由(1)知,
所以,
即,
当时,
,
当且仅当时,即时等号成立,
当时,为减函数,
所以函数的最小值为,
综上可得,当时,函数取得最小值.
【变式1】(23-24高一下·云南曲靖·期末)某乡镇企业2024年1~4月份生产的产品产量(单位:千件)与收益(单位:万元)的统计数据如下表:
月份
产品产量千件 …
收益万元 …
已知且,给出以下4个函数模型:①;②;③;④.
(1)选择一个恰当的函数模型来描述,之间的关系,并求出其解析式;
(2)已知该乡镇企业由于场地小,最多只能生产500千件,否则需要搬迁,现镇政府想使该企业的收益在10万元以上(含10万元),此企业是否应搬迁?
【答案】(1)④,
(2)应搬迁
【分析】(1)首先根据函数的性质判断符合的函数,再代入表格数据,即可求解函数的解析式;
(2)根据(1)的结果,列不等式,即可求解.
【详解】(1)由表中数据可知,收益随着产品产量的递增而递增,且增长速度越来越慢.
而①单调递减,不合题意,
③是单调递减函数,不合题意,
对于②,由题意可知,从而增长率越来越快,不合题意.
故只能选择④的模型,且.
将,代入,可得,
解得,所以,
当时,,
当时,,所以符合题意,
所以可用④来描述,之间的关系,解析式为;
(2)令,则,
又,所以此企业需要搬迁.
【变式2】(23-24高一下·湖北·阶段练习)学校为了鼓励学生课余时间积极参加体育锻炼,需要制定一个课余锻炼考核评分制度,建立一个每天得分与当天锻炼时间(单位:分钟,)的函数关系式,要求如下:
(i)函数的图象接近图示;
(ii)每天锻炼时间为0分钟时,当天得分为0分;
(iii)每天锻炼时间为9分钟时,当天得分为6分;
(iiii)每天得分最多不超过12分.
现有以下三个函数模型供选择:
①;②;③.
(1)请根据函数图像性质,结合题设条件,从中选择一个最合适的函数模型并求出解析式;
(2)若学校要求每天的得分不少于9分,求每天至少锻炼多少分钟?
(参考值:)
【答案】(1)选择③,;
(2)29.25.
【分析】(1)根据三种函数的图象特征选择合适的函数模型,然后代入点和解方程组即可得解析式;
(2)根据题意解对数不等式即可.
【详解】(1)模型①,由图象过点,
得,解得, ,在原点附近增长速度先快后慢,不符合;
模型②为爆炸增长型函数,不符合,
故选模型③.
由题知,,解得,
所以.
(2)由(1)知,,
令,得,解得,
所以,若每天的得分不少于9分,至少每天要锻炼29.25分钟.
【变式3】(24-25高一上·全国·课后作业)人们早就发现了放射性物质的衰减现象.在考古工作中,常用的含量来确定有机物的年代.已知放射性物质的衰减服从指数规律:,其中t表示衰减的时间,表示放射性物质的原始质量,表示经衰减了t年后剩余的质量.为计算衰减的年代,通常给出该物质质量衰减一半的时间,称其为该物质的半衰期.的半衰期大约是5730年.人们又知道,放射性物质的衰减速度与其质量成正比.1950年,在伊拉克发现一根古巴比伦王国时期刻有汉谟拉比王朝字样的木炭,当时测定,其的衰减速度为4.09个/(),而新砍伐树木烧成的木炭中的衰减速度为6.68个/().请估算出汉谟拉比王朝所在年代.(参考数据:)
【答案】公元前2100年
【分析】首先由衰减规律得,从而,进一步由题意得,即,解指数方程即可进一步求解.
【详解】因为的半衰期大约是5730年,所以由衰减规律,得.
解得.因此的衰减规律服从指数型函数.
设发现汉谟拉比王朝字样的木炭时(1950年),该木炭已衰减了年.
因为放射性物质的衰减速度与其质量成正比,所以,
于是.
两边取以2为底的对数,得.
解得.
所以该木炭已衰减了约4055年,即汉谟拉比王朝大约存在于公元前2100年.
题型09数形结合的思想
【典例1】(23-24高二下·海南·期末)已知函数若关于的方程有两个不同的实根,则实数的取值范围是( )
A. B. C. D.
【答案】D
【分析】先进行变形,关于的方程有两个不同的实根,即关于的方程有两个不同的实根.即与有两个不同的交点.研究图像,数形结合可解.
【详解】,则关于的方程有两个不同的实根,即关于的方程有两个不同的实根.
即与有两个不同的交点.
令,,解得.
递增,递减,
则有极大值.,
则可画出的草图.与有两个不同的交点.
则实数的取值范围是.
故选:D.
【典例2】(23-24高二下·浙江杭州·期中)已知函数,若对于正数,直线与函数的图像恰好有个不同的交点,则 .
【答案】
【分析】由题意首先确定函数的性质,然后结合直线与圆的位置关系得到的表达式,最后裂项求和即可求得的值.
【详解】当时,,即,
表示以为圆心,为半径的圆在轴(含轴)的上半部分,
当时,,函数周期为4,
如图作出函数的图象,
因为与函数恰有个不同的交点,
根据图象知,直线与第个半圆相切,
第个半圆的圆心为,半径为,
故直线的斜率,
所以,
所以.
故答案为:.
【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解
【典例3】(23-24高二下·山东滨州·期末)设函数 若关于的方程有5个不相等的实数根,则实数的取值范围是 .
【答案】
【分析】令,代入方程解得或,则和共有5个不同的实数根.作出的图象,观察图象即可求出的取值范围.
【详解】令,则,即,即,解得或,则和共有5个不同的实数根.作出的图象,如图:
由图可知,,解得.
故答案为:.
【变式1】(23-24高一下·云南·期末)设,若关于的方程恰有5个不同实数解,则实数的取值范围是( )
A. B. C. D.
【答案】D
【分析】化方程为或,分析函数的性质,再利用数形结合法求出的范围.
【详解】方程化为,解得或,
函数在上单调递增,函数值集合为,在上单调递减,函数值集合为,
在上单调递增,函数值集合为,
在同一坐标系内作出直线与函数的图象,
显然直线与函数的图象有两个交点,
由关于的方程恰有5个不同实数解,则直线与函数的图象有3个交点,
此时,所以实数的取值范围是.
故选:B
【点睛】思路点睛:研究方程根的情况,可以通过转化,利用导数研究函数的单调性、最值等,借助数形结合思想分析问题,使问题的求解有一个清晰、直观的整体展现.
【变式2】(2024·天津河东·二模)已知函数,,若方程恰有2个不同的实数根,则实数的取值范围为 .
【答案】,,.
【分析】作出的图象,分、、、及五种情况,分别作出图象进行讨论,即可得答案.
【详解】依题意画出的图象如图所示:
因为函数,
所以,
当直线与相切时,
由,得,
,解得,
由图可知,①当时,函数的图象与的图象无交点,不满足题意;
②当时,函数的图象与的图象交于点,不满足题意;
③时,当经过函数图象上的点时,恰好经过函数图象上的点,
则要使方根恰有2个不同的实数根,
只需,即,故;
④当时,函数的图象与的图象有3个交点,不满足题意;
⑤当时,函数的图象与的图象有2个交点,满足题意.
综上,或.
所以的取值范围为:,,.
故答案为:,,.
【点睛】方法点睛:求解函数零点个数的常用方法:
(1) 直接法:令则方程实根的个数就是函数零点的个;
(2) 零点存在性定理法:判断函数在区间上是连续不断的曲线,且再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数;(3) 数形结合法:转化为两个函数的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,在一个区间上单调的函数在该区间内至多只有一个零点,在确定函数零点的唯一性时往往要利用函数的单调性,确定函数零点所在区间主要利用函数零点存在定理,有时可结合函数的图象辅助解题.
【变式3】(23-24高二下·湖南·期末)已知函数,且时,,则的取值范围为 .
【答案】
【分析】作出函数的图象,结合对数的运算性质求出,根据二次函数的对称性求出,再结合二次函数的性质即可得解.
【详解】作出函数的图象,如图所示,
因为时,,
由图可知,,
则,
即,所以,所以,
由函数关于对称,可得,
所以,
因为,所以,
即的取值范围为.
故答案为:.
【点睛】关键点点睛:作出函数的图象,结合对数的运算性质求出,根据二次函数的对称性求出,是解决本题的关键.
题型10分类讨论的思想
【典例1】(24-25高一上·上海·课堂例题)设(且),求的取值范围.
【答案】答案见解析
【分析】分类讨论和两种情况,结合指数函数的单调性和一元二次方程的解法即可求解
【详解】当时,由可得,
即,即,解得或;
当时,由可得,
即,即,解得.
综上所述,当时,的取值范围是;
当时,的取值范围是.
【典例2】(23-24高二下·山东青岛·期末)已知,,(且).
(1)若,,解不等式;
(2)若.
(ⅰ)当时,判断函数的奇偶性,并说明理由;
(ⅱ)当时,若的最小值为,求的值.
【答案】(1);
(2)(ⅰ)为偶函数,理由见解析;(ⅱ).
【分析】(1)时,由,可得,根据对数函数的单调性即可求解;
(2)(ⅰ)时,,判断其奇偶性即可;
(ⅱ)时,函数的定义域为,且,根据二次函数及对数函数的性质分类讨论即可求解.
【详解】(1)若,则,,
由,可得.
因为,所以,解得.
所以不等式的解集为.
(2)(ⅰ)若,则,
由,可得,即函数的定义域为,关于原点对称,
又,
所以函数为定义在上的偶函数.
(ⅱ)当时,,
令,解得,即函数的定义域为.
又
.
因为,所以,所以,
所以.
因为且,
所以当时,,
因为的最小值为,所以,解得.
当时,,不存在最小值,舍去.
综上所述,.
【变式1】(2024高三下·全国·专题练习)函数(,且)在上的最大值为13,求实数a的值.
【答案】3或
【分析】令,讨论或,求出t的取值范围,再利用二次函数的单调性即可求解.
【详解】∵
令,则,
则,其对称轴为.
该二次函数在上是增函数.
①若,由,得,
故当,即时,
,解得(舍去).
②若,由,可得,
故当,即时,
.
∴或(舍去).
综上可得或.
【变式2】(23-24高二下·山东青岛·阶段练习)已知函数.
(1)求函数的解析式;
(2)求函数的单调增区间.
【答案】(1)
(2)答案见解析
【分析】(1)将看成一个整体求解即可;
(2)利用复合函数的单调性求解即可.
【详解】(1),
所以.
(2),
所以是对称轴为,开口向上的二次函数,
且的解集为,
故在上单调递减,在单调递增.
当时,函数是增函数,故函数在上单调递减,在单调递增;
当时,函数是减函数,函数在上单调递增,在单调递减;
【变式3】(2024高三·全国·专题练习)已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
【答案】(1)
(2)不存在,理由见解析
【分析】(1)依题意可得在上恒成立,参变分离可得在上恒成立,令,,利用导数说明函数的单调性,即可求出的取值范围;
(2)由(1)同理可知,再分、两种情况讨论,结合二次函数的性质计算可得.
【详解】(1)当时,函数恒有意义,
所以在上恒成立,
即在上恒成立.
令,,
则,
所以在上单调递减,
所以,所以.
又且,所以.
(2)函数在区间上有意义,
则在上恒成立.
由(1)同理可知,,
又函数在区间上为减函数,并且最大值为.
当时,为减函数,
则且在上单调递增,
所以,即,故不存在这样的实数;
当时,为增函数,
则且在上单调递减,
所以,即,故不存在这样的实数.
综上,不存在这样的实数,使得函数在区间上为减函数,且最大值为.
题型11换元的思想
【典例1】(23-24高一下·云南曲靖·阶段练习)若函数在上是单调函数,且满足对任意,都有,则函数的零点所在的区间为( )
A. B. C. D.
【答案】D
【分析】设,根据,列出关于的方程,进而求得的值,得到的解析式,再用零点存在定理判断即可.
【详解】因为函数在上是单调函数,,
设,所以,
所以,
因为与在上单调递增,所以有唯一解,解得,
所以,
又,,
故的零点所在的区间为.
故选:B.
【典例2】(23-24高二下·宁夏银川·期末)已知函数是定义在上的奇函数.
(1)求的解析式并用定义证明的单调性;
(2)使得成立,求实数的取值范围.
【答案】(1),证明见解析
(2)
【分析】(1)根据奇函数(定义域为)的性质求出的值,再代入检验,最后根据单调性的定义证明函数的单调性;
(2)先将不等式化为,再利用换元法结合函数单调性求出的最小值即可得解.
【详解】(1)因为是定义在上的奇函数,
所以,解得,
则,
且,
所以为定义在上的奇函数,故,即.
是上的增函数,证明如下:
任取,且,
则
(2)∵在上恒成立,
又,当且仅当即时取等号,
∴的最小值为,∴.
【变式2】(23-24高三下·北京·阶段练习)已知函数(为实常数).
(1)若函数为奇函数,求的值;
(2)在(1)的条件下,对任意,不等式恒成立,求实数的最大值.
【答案】(1)
(2)1
【分析】(1)若函数为奇函数,由奇函数的性质可求得,并代入检验;
(2)对任意,不等式恒成立,化简不等式参变分离,构造新函数,利用换元法和对勾函数的单调性求出最值,代入得出实数u的最大值.
【详解】(1)由题意可知:的定义域为,
若函数为奇函数,则,解得,
此时,
则,
即,可知为奇函数,则符合题意,
综上所述:.
(2)由(1)可知,
由不等式,得,
原题意等价于,
因为,令,
则
又因为函数在单调递增,则,
可得,所以实数的最大值为1.
21世纪教育网(www.21cnjy.com)
题型01有关指数、对数的运算
【典例1】(23-24高二下·天津·期末)计算下列各式的值:
(1);
(2);
(3)若,,求的值.
【典例2】(24-25高一上·上海·单元测试)计算:
(1);
(2).
【典例3】(2024高三·全国·专题练习)计算下列各式.
(1);
(2)
(3);
(4);
(5);
(6);
(7)已知,求的值.
【变式1】(23-24高二下·宁夏银川·期末)计算
(1)
(2)
【变式2】(24-25高一上·上海·随堂练习)计算下列各式的值:
(1);
(2).
【变式3】(23-24高二下·天津·阶段练习)计算:
(1);
(2).
题型02数的大小比较问题
【典例1】(云南省楚雄彝族自治州2023-2024学年高一下学期期末教育学业质量监测数学试题)已知,则( )
A. B. C. D.
【典例2】(湖南省张家界市2023-2024学年高二下学期期末考试数学试题)已知,,,则( )
A. B.
C. D.
【典例3】(23-24高二下·黑龙江·期末)若,,,则( )
A. B.
C. D.
【变式1】(23-24高二下·北京朝阳·期末)已知,,,则,,的大小关系为( )
A. B. C. D.
【变式2】(2024高三·天津·专题练习)若,,,则,,的大小关系为( )
A. B. C. D.
【变式3】(23-24高二下·北京通州·期末)已知,,,则( )
A. B. C. D.
题型03定义域问题
【典例1】(23-24高一上·安徽·期中)函数的定义域为( )
A. B. C. D.
【典例2】(24-25高一上·上海·课后作业)函数的定义域为 .
【典例3】(24-25高一上·上海·课后作业)已知函数,其定义域为,求的取值范围.
【变式1】(23-24高二下·北京石景山·期末)函数的定义域为 .
【变式2】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2);
(3).
【变式3】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2).
题型04值域问题
【典例1】(21-22高一上·内蒙古赤峰·期中)函数的最大值为 .
【典例2】(2024·上海·模拟预测)函数的最小值为 .
【典例3】(23-24高一上·河南省直辖县级单位·阶段练习)求函数的单调区间与值域.
【变式1】(2024高三·全国·专题练习)已知函数的值域为R,则实数a的取值范围是( )
A. B.
C. D.
【变式2】(24-25高一上·上海·随堂练习)函数的最小值为 .
【变式3】(2024高一上·全国·专题练习)求函数 的值域.
题型05指数(型)函数,对数(型)函数的图象
【典例1】(23-24高一上·云南昆明·期末)如图所示,函数图像①②③④⑤⑥⑦⑧中不属于函数:,的是( )
A.①⑤ B.②⑥
C.③⑦ D.④⑧
【典例2】(24-25高一上·全国·课后作业)当时,在同一平面直角坐标系中,函数与的图象是( ).
A. B.
C. D.
【典例3】(23-24高一下·河北石家庄·开学考试)在同一平面直角坐标系中,函数,(且)的图象可能是( )
A. B.
C. D.
【变式1】(23-24高一上·四川攀枝花·阶段练习)已知且,则函数与在同一直角坐标系中的图象大致是( )
A. B.
C. D.
【变式2】(23-24高一上·内蒙古呼伦贝尔·期末)当时,在同一坐标系中,函数与的图像是( )
A. B.
C. D.
【变式3】(23-24高一上·江西景德镇·期末)已知(且且),则函数与的图象可能是( )
A. B.
C. D.
题型06指数(型)函数,对数(型)函数的性质
【典例1】(2024高三·全国·专题练习)已知函数,若,则实数的取值范围是 .
【典例2】(23-24高一下·安徽阜阳·期末)已知函数为奇函数.
(1)求的值;
(2)若对任意的,关于的不等式恒成立,求正实数的取值范围.
【典例3】(23-24高二下·浙江·期中)已知函数为偶函数.
(1)求的值;
(2)若,判断在的单调性,并用定义法给出证明;
(3)若在区间上恒成立,求的取值范围.
【变式1】(23-24高一下·山西大同·期末)已知函数,,若对于任意,存在,使得,则实数m的取值范围为 .
【变式2】(23-24高二下·天津和平·期末)已知函数(且)是定义在上的奇函数.
(1)求的值;
(2)若,且对于,不等式成立,求实数的取值范围.
【变式3】(23-24高二下·山西吕梁·期末)已知函数,其中.
(1)若,求函数的定义域;
(2)当时,恒成立,求实数的取值范围.
题型07函数与方程
【典例1】(24-25高一上·上海·单元测试)已知函数,若函数恰有一个零点,求实数的取值范围.
【典例2】(23-24高一下·贵州遵义·阶段练习)已知函数.
(1)若在上为增函数,求的取值范围;
(2)若函数在上恰有两个零点,求的取值范围.
【典例3】(23-24高一上·湖南益阳·期末)已知函数,其中,且为奇函数.
(1)求a的值;
(2)若,,,求集合M;
(3)若函数,讨论函数(k为常数)的零点个数.
【变式1】(23-24高一下·安徽滁州·阶段练习)已知函数.
(1)讨论的单调性;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
【变式2】(2024高一·全国·专题练习)已知函数在区间上的最大值为,最小值为.
(1)求实数,的值;
(2)若方程在上有两个不同的实数解,求的取值范围.
【变式3】(2024高二·全国)已知,
(1)若函数与在时有相同的值域,求的取值范围;
(2)若方程在上有两个不同的根,求的取值范围,并证明:.
题型08函数模型及其应用
【典例1】(23-24高一上·浙江丽水·期末)丽水市某革命老区因地制宜发展生态农业,打造“生态特色水果示范区”.该地区某水果树的单株年产量(单位:千克)与单株施肥量(单位:千克)之间的关系为,且单株投入的年平均成本为元.若这种水果的市场售价为元/千克,且水果销路畅通.记该水果树的单株年利润为(单位:元).
(1)求函数的解析式;
(2)求单株施肥量为多少千克时,该水果树的单株年利润最大?最大利润是多少?
【典例2】(23-24高一下·云南昆明·期中)2023年9月17日,联合国教科文组织第45届世界遗产大会通过决议,将中国“普洱景迈山古茶树文化景观”列入《世界遗产名录》,成为全球首个茶主题世界文化遗产.经验表明,某种普洱茶用的水冲泡,等茶水温度降至饮用,口感最佳.某科学兴趣小组为探究在室温条件下,刚泡好的茶水达到最佳饮用口感的放置时间,每隔1分钟测量一次茶水温度,得到茶水温度y(单位:℃)与时间t(单位:分钟)的部分数据如下表所示:
时间t/分钟 0 1 2 3 4 5
水温 95.00 88.00 81.70 76.03 70.93 66.33
(1)给出下列三种函数模型:①,②,③,请根据上表中的数据,选出你认为最符合实际的函数模型,简单叙述理由,并利用表中前3组数据求出相应的解析式;
(2)根据(1)中所求模型,求刚泡好的普洱茶达到最佳饮用口感的放置时间(精确到0.1).(参考数据:)
【典例3】(22-23高一上·河南南阳·期末)某城市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),
每件的销售价格)(单位:元)与时间(单位:天)的函数关系近似满足(为常数,且),日销售量(单位:件)与时间(单位:天)的部分数据如下表所示:
10 15 20 25 30
50 55 60 55 50
已知第10天的日销售收入为505元.
(1)给出以下四个函数模型:①;②;③;④.请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量与时间的变化关系,并求出该函数的解析式;
(2)设该工艺品的日销售收入为(单位:元),求的最小值.
【变式1】(23-24高一下·云南曲靖·期末)某乡镇企业2024年1~4月份生产的产品产量(单位:千件)与收益(单位:万元)的统计数据如下表:
月份
产品产量千件 …
收益万元 …
已知且,给出以下4个函数模型:①;②;③;④.
(1)选择一个恰当的函数模型来描述,之间的关系,并求出其解析式;
(2)已知该乡镇企业由于场地小,最多只能生产500千件,否则需要搬迁,现镇政府想使该企业的收益在10万元以上(含10万元),此企业是否应搬迁?
【变式2】(23-24高一下·湖北·阶段练习)学校为了鼓励学生课余时间积极参加体育锻炼,需要制定一个课余锻炼考核评分制度,建立一个每天得分与当天锻炼时间(单位:分钟,)的函数关系式,要求如下:
(i)函数的图象接近图示;
(ii)每天锻炼时间为0分钟时,当天得分为0分;
(iii)每天锻炼时间为9分钟时,当天得分为6分;
(iiii)每天得分最多不超过12分.
现有以下三个函数模型供选择:
①;②;③.
(1)请根据函数图像性质,结合题设条件,从中选择一个最合适的函数模型并求出解析式;
(2)若学校要求每天的得分不少于9分,求每天至少锻炼多少分钟?
(参考值:)
【变式3】(24-25高一上·全国·课后作业)人们早就发现了放射性物质的衰减现象.在考古工作中,常用的含量来确定有机物的年代.已知放射性物质的衰减服从指数规律:,其中t表示衰减的时间,表示放射性物质的原始质量,表示经衰减了t年后剩余的质量.为计算衰减的年代,通常给出该物质质量衰减一半的时间,称其为该物质的半衰期.的半衰期大约是5730年.人们又知道,放射性物质的衰减速度与其质量成正比.1950年,在伊拉克发现一根古巴比伦王国时期刻有汉谟拉比王朝字样的木炭,当时测定,其的衰减速度为4.09个/(),而新砍伐树木烧成的木炭中的衰减速度为6.68个/().请估算出汉谟拉比王朝所在年代.(参考数据:)
题型09数形结合的思想
【典例1】(23-24高二下·海南·期末)已知函数若关于的方程有两个不同的实根,则实数的取值范围是( )
A. B. C. D.
【典例2】(23-24高二下·浙江杭州·期中)已知函数,若对于正数,直线与函数的图像恰好有个不同的交点,则 .
【典例3】(23-24高二下·山东滨州·期末)设函数 若关于的方程有5个不相等的实数根,则实数的取值范围是 .
【变式1】(2024高三下·全国·专题练习)函数(,且)在上的最大值为13,求实数a的值.
【变式2】(23-24高二下·山东青岛·阶段练习)已知函数.
(1)求函数的解析式;
(2)求函数的单调增区间.
【变式3】(2024高三·全国·专题练习)已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
题型11换元的思想
【典例1】(23-24高一下·云南曲靖·阶段练习)若函数在上是单调函数,且满足对任意,都有,则函数的零点所在的区间为( )
A. B. C. D.
【典例2】(23-24高二下·宁夏银川·期末)已知函数是定义在上的奇函数.
(1)求的解析式并用定义证明的单调性;
(2)使得成立,求实数的取值范围.
【变式1】(24-25高一上·上海·随堂练习)函数的定义域为.
(1)设,求的取值范围;
(2)若恒成立,求的范围.
【变式2】(23-24高三下·北京·阶段练习)已知函数(为实常数).
(1)若函数为奇函数,求的值;
(2)在(1)的条件下,对任意,不等式恒成立,求实数的最大值.
第09讲 第四章 指数函数与对数函数 章末题型大总结
题型01有关指数、对数的运算
【典例1】(23-24高二下·天津·期末)计算下列各式的值:
(1);
(2);
(3)若,,求的值.
【答案】(1)
(2)
(3)1
【分析】(1)根据幂的运算法则计算;
(2)利用换底公式后计算;
(3)指数式与对数式互化后,由对数运算法则、换底公式求解.
【详解】(1)
;
(2)
;
(3),又,
所以.
【典例2】(24-25高一上·上海·单元测试)计算:
(1);
(2).
【答案】(1)
(2)4
【分析】(1)根据二次根式、分数指数幂和对数的运算性质求解;
(2)根据对数的运算性质求解.
【详解】(1)原式
;
(2)原式.
【典例3】(2024高三·全国·专题练习)计算下列各式.
(1);
(2)
(3);
(4);
(5);
(6);
(7)已知,求的值.
【答案】(1)
(2)
(3)4
(4)
(5)
(6)
(7)2
【分析】根据题意,结合指数幂的运算法则和运算性质,逐个计算,即可求解.
【详解】(1)解:由指数幂的运算法则和运算性质,可得:
.
(2)解:由指数幂的运算法则和运算性质,可得:
.
(3)解:由指数幂的运算法则和运算性质,可得:
.
(4)解:由指数幂的运算法则和运算性质,可得:
.
(5)解:由指数幂的运算法则和运算性质,可得:
.
(6)解:由指数幂的运算法则和运算性质,可得:
.
(7)解:因为,所以,所以,
则,
所以.
【变式1】(23-24高二下·宁夏银川·期末)计算
(1)
(2)
【答案】(1)
(2)
【分析】(1)由指数幂的运算性质直接计算即可;
(2)由对数的运算性质直接计算即可.
【详解】(1)
.
(2).
【变式2】(24-25高一上·上海·随堂练习)计算下列各式的值:
(1);
(2).
【答案】(1)2
(2)1
【分析】(1)(2)根据对数运算律计算即可;
【详解】(1)原式
.
(2)原式
.
【变式3】(23-24高二下·天津·阶段练习)计算:
(1);
(2).
【答案】(1)
(2)
【分析】(1)根据指数幂的运算法则计算可得;
(2)根据对数的运算性质及换底公式计算可得.
【详解】(1)
.
(2)
.
题型02数的大小比较问题
【典例1】(云南省楚雄彝族自治州2023-2024学年高一下学期期末教育学业质量监测数学试题)已知,则( )
A. B. C. D.
【答案】A
【分析】根据对数函数和指数函数的单调性比较大小.
【详解】因为在上单调递增,且,
所以,所以,即,
因为在上递增,且,
所以,即,
因为在上单调递减,且,
所以,所以,即,
所以.
故选:A
【典例2】(湖南省张家界市2023-2024学年高二下学期期末考试数学试题)已知,,,则( )
A. B.
C. D.
【答案】D
【分析】根据指对数运算公式及指数函数与对数函数的单调性可比较大小.
【详解】由,
又,且,
所以,
又,
所以,
故选:B.
【典例3】(23-24高二下·黑龙江·期末)若,,,则( )
A. B.
C. D.
【答案】A
【分析】根据对数运算,结合指数函数和对数函数的单调性,转化为和特殊值比较大小,即可判断.,,
【详解】因为,,所以.
故选:A
【变式1】(23-24高二下·北京朝阳·期末)已知,,,则,,的大小关系为( )
A. B. C. D.
【答案】D
【分析】根据对数的运算性质及对数函数的性质计算可得.
【详解】因为,
所以,
所以.
故选:D
【变式2】(2024高三·天津·专题练习)若,,,则,,的大小关系为( )
A. B. C. D.
【答案】D
【分析】因为在上递增,得出,又因在上递增,可得.
【详解】在上递增,且,
所以,所以,即,
因为在上递增,且,
所以,
即,所以,
故选:.
【变式3】(23-24高二下·北京通州·期末)已知,,,则( )
A. B. C. D.
【答案】A
【分析】根据指数函数、对数函数的性质判断即可.
【详解】因为,,
即,,
所以.
故选:A
题型03定义域问题
【典例1】(23-24高一上·安徽·期中)函数的定义域为( )
A. B. C. D.
【答案】A
【分析】根据指数函数的单调性及二次根式的意义可求得原函数的定义域.
【详解】对于函数,有,可得,解得,
因此,函数的定义域为.
故选:A.
【典例2】(24-25高一上·上海·课后作业)函数的定义域为 .
【答案】
【分析】根据具体函数的定义域,结合对数函数的性质列式求解即可.
【详解】函数的定义域需满足不等式,
得或,
所以函数的定义域是.
故答案为:
【典例3】(24-25高一上·上海·课后作业)已知函数,其定义域为,求的取值范围.
【答案】.
【分析】根据对数的性质可得对任意的,都成立,即可利用判别式求解.
【详解】解:∵函数的定义域为,∴,对任意的都成立,
则,解得.
所以的值范围为.
【变式1】(23-24高二下·北京石景山·期末)函数的定义域为 .
【答案】
【分析】根据定义域的求解方法即可.
【详解】要使函数有意义,则,解得,
故答案为: .
【变式2】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2);
(3).
【答案】(1)
(2)
(3)
【分析】(1)(3)根据二次根式与指数函数性质求解;
(2)利用指数函数性质结合分式的定义求解;
【详解】(1)由题意,,,所以定义域为;
(2)由题意,即,所以定义域为;
(3)由题意,即,,,所以定义域为.
【变式3】(24-25高一上·上海·课堂例题)求下列函数的定义域:
(1);
(2).
【答案】(1)
(2)且.
【分析】(1)根据对数函数真数大于0得到不等式,求出答案;
(2)根据分母不为0和二次根式被开方数非负得到不等式,求出答案.
【详解】(1)要使函数有意义,则,解得,所以函数的定义域为.
(2)由题意知解得且,,
所以函数的定义域为且.
题型04值域问题
【典例1】(21-22高一上·内蒙古赤峰·期中)函数的最大值为 .
【答案】5
【分析】利用换元法,结合指数函数与二次函数的性质即可得解.
【详解】因为,
令,则,,
当,即时,取得最大值5.
故答案为:5.
【典例2】(2024·上海·模拟预测)函数的最小值为 .
【答案】
【分析】根据对数的运算性质将函数化简为,再结合二次函数的性质计算可得.
【详解】因为
,
当,即时,取到最小值,且.
故答案为:
【典例3】(23-24高一上·河南省直辖县级单位·阶段练习)求函数的单调区间与值域.
【答案】单调减区间是,单调增区间是;值域是
【分析】单调性根据复合函数的单调性同增异减得出,值域根据换元法得出.
【详解】函数,
设.
,
当时,,
,即.
函数在上的值域是.
又原函数是由和两个函数复合而成,
第一个函数是单调减函数,第二个函数在区间上是单调增函数,在区间上是单调减函数
函数的单调减区间是,单调增区间是.
【变式1】(2024高三·全国·专题练习)已知函数的值域为R,则实数a的取值范围是( )
A. B.
C. D.
【答案】C
【分析】先求出时,,从而得到当时,的值域包含,得到不等式,求出实数a的取值范围.
【详解】当时,,又的值域为R,
故当时,的值域包含.
故,解得.
故选:C
【变式2】(24-25高一上·上海·随堂练习)函数的最小值为 .
【答案】0
【分析】利用复合函数的性质求函数的最小值,可以考虑使用换元法.
【详解】解:设,则,
的定义域为,
所以函数,在上单调递减,在上单调递增,
由复合函数的同增异减可得:在区间上单调递减,在上单调递增,
,最小值是0.
故答案为:0.
【变式3】(2024高一上·全国·专题练习)求函数 的值域.
【答案】
【分析】根据即可求解.
【详解】,
因为,
所以原函数的值域为.
题型05指数(型)函数,对数(型)函数的图象
【典例1】(23-24高一上·云南昆明·期末)如图所示,函数图像①②③④⑤⑥⑦⑧中不属于函数:,的是( )
A.①⑤ B.②⑥
C.③⑦ D.④⑧
【答案】D
【分析】根据题意,分别由指数函数的图像特点与对数函数的图像特点,即可判断.
【详解】由指数函数的图像性质可知,①②③④为指数函数图像,
且③④为单调递增的指数函数,取可知,③④分别对应,
又①④图像关于轴对称,则①对应,即②不属于;
由对数函数的图像性质可知,⑤⑥⑦⑧为对数函数图像,
其中⑦⑧为单调递减的对数函数,
由“底大图低”可知⑧对应,⑦对应,
且⑤⑧图像关于轴对称,则⑤对应,即⑥不属于;
故选:B
【典例2】(24-25高一上·全国·课后作业)当时,在同一平面直角坐标系中,函数与的图象是( ).
A. B.
C. D.
【答案】A
【分析】由对数函数指数函数单调性以及它们各自所过的定点即可得解.
【详解】当时,函数与分别在各自的定义域内单调递减、单调递增,
故可排除BCD,
且函数与图象分别过定点,经检验,A符合题意.
故选:A.
【典例3】(23-24高一下·河北石家庄·开学考试)在同一平面直角坐标系中,函数,(且)的图象可能是( )
A. B.
C. D.
【答案】D
【分析】分和进行分类讨论判断即可.
【详解】当时,与单调递增,A,B均不符合题意;
当时,与单调递减,
对于,当时,C不正确.
故选:D.
【变式1】(23-24高一上·四川攀枝花·阶段练习)已知且,则函数与在同一直角坐标系中的图象大致是( )
A. B.
C. D.
【答案】C
【分析】由已知结合两函数的单调性及恒过的定点检验各选项即可判断.
【详解】结合与可知,两函数单调性一定相反,排除选项A;
因为恒过定点,恒过定点,排除选项B,D.
故选:C.
【变式2】(23-24高一上·内蒙古呼伦贝尔·期末)当时,在同一坐标系中,函数与的图像是( )
A. B.
C. D.
【答案】D
【分析】根据指数对数函数的图象性质进行判断.
【详解】当时,
函数为单调递减的指数函数,函数为单调递减的对数函数,
观察选项可得D符合.
故选:D.
【变式3】(23-24高一上·江西景德镇·期末)已知(且且),则函数与的图象可能是( )
A. B.
C. D.
【答案】D
【分析】由对数的运算性质可得,讨论的范围,结合指数函数和对数函数的图象的单调性,即可得到答案.
【详解】由,即为,即有;
当时,,
函数在上为增函数,在为增函数,选项B满足;
当时,,
函数在上为减函数,在为减函数,
四个图象均不满足,在同一坐标系中的图象只能是B.
故选:B
题型06指数(型)函数,对数(型)函数的性质
【典例1】(2024高三·全国·专题练习)已知函数,若,则实数的取值范围是 .
【答案】.
【分析】先根据函数的解析式判断得出函数的奇偶性以及单调性.进而将原不等式转化为,即可结合函数的单调性列出不等式,求解即可得出答案.
【详解】由题意知函数定义域为R,且,
所以 为奇函数.
又函数均为R上的增函数,根据复合函数的单调性可知也为R上的增函数,
所以,为R上的函数.
由,得,所以,
解得,
故答案为:.
【典例2】(23-24高一下·安徽阜阳·期末)已知函数为奇函数.
(1)求的值;
(2)若对任意的,关于的不等式恒成立,求正实数的取值范围.
【答案】(1);
(2).
【分析】(1)利用奇函数定义列式计算即得.
(2)由(1)的结论,结合指数函数的性质求出在上的值域,换元分离参数借助函数单调性求解即得.
【详解】(1)由函数为奇函数,
得,解得,
所以.
(2)由(1)知,,当时,,则,因此,
令,,不等式,
等价于,即,而,
因此,,而函数在上单调递减,
即,从而恒成立,则,
所以正实数的取值范围是.
【典例3】(23-24高二下·浙江·期中)已知函数为偶函数.
(1)求的值;
(2)若,判断在的单调性,并用定义法给出证明;
(3)若在区间上恒成立,求的取值范围.
【答案】(1)
(2)单调递增,证明见解析
(3)
【分析】(1)根据,得到方程,求出;
(2)先得到,定义法判断函数单调性步骤,取值,作差,判号,下结论;
(3)参变分离得到,构造,换元后得到,根据单调性求出其最值,得到结论.
【详解】(1)定义域为R,
,
由于函数为偶函数,所以,
即,即,
即恒成立,
.
(2)已知函数,由于函数在上单调递增,
由第(1)问可得,因此
不妨设,,且
则
因为,因此,由因为,,因此,
所以,故,所以函数在单调递增.
(3)由题得在区间上恒成立,即在区间上恒成立,
因为,所以,所以在区间上恒成立,
令,令,
则,
因为在单调递增,
所以函数在上单调递减,故.
.
对任意的恒成立,且,
.
实数的取值范围是.
【变式1】(23-24高一下·山西大同·期末)已知函数,,若对于任意,存在,使得,则实数m的取值范围为 .
【答案】
【分析】根据给定条件,求出函数在上的最大值,探讨函数的性质,并求出在上的最大值,再由已知建立不等式求解即得.
【详解】函数,当时,,
则当,即时,;
函数,显然,
则函数的图象关于直线对称,当时,令,,
,,
由,得,则,,于是,
函数在上单调递增,则函数在上单调递增,
在上单调递减,而在上单调递减,
因此函数在上单调递减,由对称性知,在上单调递增,
则当时,,
由对于任意,存在,使得,得,解得,
所以实数m的取值范围为.
故答案为:
【点睛】结论点睛:函数的定义域为D,,
①存在常数a,b使得,则函数图象关于点对称.
②存在常数a使得,则函数图象关于直线对称.
【变式2】(23-24高二下·天津和平·期末)已知函数(且)是定义在上的奇函数.
(1)求的值;
(2)若,且对于,不等式成立,求实数的取值范围.
【答案】(1)0;
(2).
【分析】(1)由奇函数的性质得,求出值并验证即可.
(2)由,求出的范围并判断的单调性,再脱去法则,参变分离求出函数的最小值即可.
【详解】(1)由是定义在上的奇函数,得,解得,
当时,,,则为上的奇函数,
所以.
(2)由(1)知,由,得,于是,
显然函数是上的单调递增函数,
又是定义在上的奇函数,由,得,
即,因此对,成立,当时,成立,
则对,,
而,当且仅当,即时取等号,从而,
所以实数的取值范围.
【变式3】(23-24高二下·山西吕梁·期末)已知函数,其中.
(1)若,求函数的定义域;
(2)当时,恒成立,求实数的取值范围.
【答案】(1)
(2)
【分析】(1)由真数大于0列出不等式即可求解;
(2)先根据函数为单调递增函数,将转化为,根据题意可转化为在上最小值大于0,然后结合二次函数的性质即可求得.
【详解】(1)当时,,
由得,
故或,
得或,
故函数的定义域为;
(2)由得,
得,
即,
设,
因,故,
所以当时,恒成立,
即为在上最小值大于0,
函数的对称轴为,
当即时,函数在上单调递增,
此时,得,
即满足题意;
当,即时,函数在对称轴取得最小值,
此时,得,
即满足题意;
故的取值范围为.
题型07函数与方程
【典例1】(24-25高一上·上海·单元测试)已知函数,若函数恰有一个零点,求实数的取值范围.
【答案】或
【分析】作出的函数图象,根据图象判断的值.
【详解】解:令得,作出的函数图像如图所示.
由图像可知当或时,只有一解,
此时恰有一个零点.
【典例2】(23-24高一下·贵州遵义·阶段练习)已知函数.
(1)若在上为增函数,求的取值范围;
(2)若函数在上恰有两个零点,求的取值范围.
【答案】(1);
(2).
【分析】(1)根据已知,利用复合函数的单调性和对数函数的定义域及二次函数的单调性,列式即可求出a的取值范围.
(2)利用函数零点的意义,结合对数运算,把问题转化为一元二次方程的实根分布求解.
【详解】(1)令,显然函数在上单调递增,
函数在及右侧区间上单调递增,
而在上为增函数,则,解得,
所以的取值范围是.
(2)由,得,
由函数在上恰有两个零点,得在上有两个不等实根,
于是,解得,
所以的取值范围是.
【典例3】(23-24高一上·湖南益阳·期末)已知函数,其中,且为奇函数.
(1)求a的值;
(2)若,,,求集合M;
(3)若函数,讨论函数(k为常数)的零点个数.
【答案】(1)1
(2)
(3)答案见解析
【分析】(1)根据函数奇偶性定义列出方程求解并检验即得;
(2)先由函数的单调性和奇偶性推导函数的单调性和奇偶性,利用函数奇偶性化简为,利用单调性求得的范围即得.
(3)依题求出,由化简得,就分成和两种情况,讨论方程的解的情况即得.
【详解】(1)因为函数为奇函数,
,
,解得.又,.
经检验,符合题意.
(2)由(1)得,则,
由,因函数为奇函数,
,即为奇函数.
又,
因在上单调递减且为正数,又在定义域内为增函数,
则在上单调递减,故在上单调递减;
由.
,解得:.故集合.
(3),且,
,且,
令.
①当时,有,
.
由得,即.
当时,方程在无实数解.
当时,由得,由,解得.
即当时,,而当时,.
所以,当或或时,函数在只有一个零点.
当且时,函数在有两个零点:和.
②当时,有,.
当时,函数在没有零点.
当时,,由得或.
所以,当或时,函数在有一个零点;
当时,函数在没有零点.
综上所述,当时,函数有且只有一个零点;
当时,函数有两个零点.
【点睛】方法点睛:本题主要考查利用函数的性质求解不等式和判断函数的零点情况,属于难题.
对于抽象不等式的解法,一般从判断函数的奇偶性和单调性入手,将不等式等价变换,将其化成具体不等式组求解;对于含参函数的零点个数问题,一般是将其转化成方程的解的个数或者两函数的图象交点个数解决.
【变式1】(23-24高一下·安徽滁州·阶段练习)已知函数.
(1)讨论的单调性;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
【答案】(1)在和上单调递增,在上单调递减.
(2)
【分析】(1)直接对两段分别研究单调性即可;
(2)画出函数的图象与直线的图象,由数形结合即可求解.
【详解】(1)当时,由单调递增,知在上单调递增;
当时,有,所以在上单调递增;
当时,是二次函数,最小值点是,故在上单调递减,在上单调递增.
综上,在和上单调递增,在上单调递减.
(2)在同一平面直角坐标系中画出函数的图象与直线的图象,如图所示,
由图可知若关于的方程有三个不同的实根,
当且仅当的取值范围是.
【变式2】(2024高一·全国·专题练习)已知函数在区间上的最大值为,最小值为.
(1)求实数,的值;
(2)若方程在上有两个不同的实数解,求的取值范围.
【答案】(1),
(2)
【分析】(1)令,得到,再利用二次函数的性质及条件,即可求出结果;
(2)由(1)及条件得到,令,分离常量得到,再利用函数的单调性,即可求出结果.
【详解】(1)设,则,
因为,对称轴为,所以当,①,
当,②,由①②解得,.
(2)由(1)知,所以,
即,设,得到,即,
又函数在单调递减,在上单调递增,
当时,,又当时,,当时,,
所以要使方程有两个不同的实数解,则.
【变式3】(2024高二·全国)已知,
(1)若函数与在时有相同的值域,求的取值范围;
(2)若方程在上有两个不同的根,求的取值范围,并证明:.
【答案】(1)
(2),证明见解析
【分析】(1)由题意知,求得的取值范围;
(2)令,经判断,可得, ,可得的范围. 消去得证得.
【详解】(1)当时,函数的图象是开口向上,
且对称轴为的抛物线,的值域为,
所以的值域也为的充要条件是,
即,或,
即的取值范围为.
(2),即,
由分析知,不妨设,
令
因为在上是单调函数,
所以在上至多有一个解.
若,即就是的解,
所以,与题设矛盾.因此,
由得,所以,
由得,所以,
综上,当时,方程在上有两个解,
由和,消去得,
由,得.
题型08函数模型及其应用
【典例1】(23-24高一上·浙江丽水·期末)丽水市某革命老区因地制宜发展生态农业,打造“生态特色水果示范区”.该地区某水果树的单株年产量(单位:千克)与单株施肥量(单位:千克)之间的关系为,且单株投入的年平均成本为元.若这种水果的市场售价为元/千克,且水果销路畅通.记该水果树的单株年利润为(单位:元).
(1)求函数的解析式;
(2)求单株施肥量为多少千克时,该水果树的单株年利润最大?最大利润是多少?
【答案】(1)
(2)施肥量为时,单株年利润最大为390元
【分析】(1)由利润=单株产量售价成本,结合分段函数即可求解;
(2)结合二次函数和基本不等式性质分别求出和时对应的,即可得解.
【详解】(1)当时,,
当时,,
故;
(2)当时,的对称轴为,最大值为,
当时,,
当且仅当时,等号成立,
综上施肥量为时,单株年利润最大为390元.
【典例2】(23-24高一下·云南昆明·期中)2023年9月17日,联合国教科文组织第45届世界遗产大会通过决议,将中国“普洱景迈山古茶树文化景观”列入《世界遗产名录》,成为全球首个茶主题世界文化遗产.经验表明,某种普洱茶用的水冲泡,等茶水温度降至饮用,口感最佳.某科学兴趣小组为探究在室温条件下,刚泡好的茶水达到最佳饮用口感的放置时间,每隔1分钟测量一次茶水温度,得到茶水温度y(单位:℃)与时间t(单位:分钟)的部分数据如下表所示:
时间t/分钟 0 1 2 3 4 5
水温 95.00 88.00 81.70 76.03 70.93 66.33
(1)给出下列三种函数模型:①,②,③,请根据上表中的数据,选出你认为最符合实际的函数模型,简单叙述理由,并利用表中前3组数据求出相应的解析式;
(2)根据(1)中所求模型,求刚泡好的普洱茶达到最佳饮用口感的放置时间(精确到0.1).(参考数据:)
【答案】(1)选模型②,理由见解析,解析式为
(2).
【分析】(1)由表格数据可知,函数单调递减且递减速度逐渐变慢,故模型①③不符合,选模型②,把前3组数据代入求出,,的值,即可得到函数解析式;
(2)令,结合对数的运算性质求出的值即可.
【详解】(1)由表格数据可知,函数单调递减且递减速度逐渐变慢,
模型③为单调递增的函数,不符合,
模型①为直线型,不符合递减速度逐渐变慢,
故模型①③不符合,选模型②,
则,解得,
所以;
(2)令,则,
所以,
即刚泡好的普洱茶达到最佳饮用口感的放置时间为.
【典例3】(22-23高一上·河南南阳·期末)某城市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),
每件的销售价格)(单位:元)与时间(单位:天)的函数关系近似满足(为常数,且),日销售量(单位:件)与时间(单位:天)的部分数据如下表所示:
10 15 20 25 30
50 55 60 55 50
已知第10天的日销售收入为505元.
(1)给出以下四个函数模型:①;②;③;④.请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量与时间的变化关系,并求出该函数的解析式;
(2)设该工艺品的日销售收入为(单位:元),求的最小值.
【答案】(1)选②,
(2)
【分析】(1)由第10天的日销售收入为505元,求出,再根据表中数据可知时间变换时,先增后减,则选模型②,再利用待定系数法求出参数,即可得解;
(2)分和,两种情况讨论,结合基本不等式和函数的单调性即可得出答案.
【详解】(1)因为第10天的日销售收入为505元,
则,解得,
由表格中的数据知,当时间变换时,先增后减,
函数模型:①;③;④都是单调函数,
所以选择模型②:,
由,可得,解得,
由,解得,
所以日销售量与时间的变化的关系式为;
(2)由(1)知,
所以,
即,
当时,
,
当且仅当时,即时等号成立,
当时,为减函数,
所以函数的最小值为,
综上可得,当时,函数取得最小值.
【变式1】(23-24高一下·云南曲靖·期末)某乡镇企业2024年1~4月份生产的产品产量(单位:千件)与收益(单位:万元)的统计数据如下表:
月份
产品产量千件 …
收益万元 …
已知且,给出以下4个函数模型:①;②;③;④.
(1)选择一个恰当的函数模型来描述,之间的关系,并求出其解析式;
(2)已知该乡镇企业由于场地小,最多只能生产500千件,否则需要搬迁,现镇政府想使该企业的收益在10万元以上(含10万元),此企业是否应搬迁?
【答案】(1)④,
(2)应搬迁
【分析】(1)首先根据函数的性质判断符合的函数,再代入表格数据,即可求解函数的解析式;
(2)根据(1)的结果,列不等式,即可求解.
【详解】(1)由表中数据可知,收益随着产品产量的递增而递增,且增长速度越来越慢.
而①单调递减,不合题意,
③是单调递减函数,不合题意,
对于②,由题意可知,从而增长率越来越快,不合题意.
故只能选择④的模型,且.
将,代入,可得,
解得,所以,
当时,,
当时,,所以符合题意,
所以可用④来描述,之间的关系,解析式为;
(2)令,则,
又,所以此企业需要搬迁.
【变式2】(23-24高一下·湖北·阶段练习)学校为了鼓励学生课余时间积极参加体育锻炼,需要制定一个课余锻炼考核评分制度,建立一个每天得分与当天锻炼时间(单位:分钟,)的函数关系式,要求如下:
(i)函数的图象接近图示;
(ii)每天锻炼时间为0分钟时,当天得分为0分;
(iii)每天锻炼时间为9分钟时,当天得分为6分;
(iiii)每天得分最多不超过12分.
现有以下三个函数模型供选择:
①;②;③.
(1)请根据函数图像性质,结合题设条件,从中选择一个最合适的函数模型并求出解析式;
(2)若学校要求每天的得分不少于9分,求每天至少锻炼多少分钟?
(参考值:)
【答案】(1)选择③,;
(2)29.25.
【分析】(1)根据三种函数的图象特征选择合适的函数模型,然后代入点和解方程组即可得解析式;
(2)根据题意解对数不等式即可.
【详解】(1)模型①,由图象过点,
得,解得, ,在原点附近增长速度先快后慢,不符合;
模型②为爆炸增长型函数,不符合,
故选模型③.
由题知,,解得,
所以.
(2)由(1)知,,
令,得,解得,
所以,若每天的得分不少于9分,至少每天要锻炼29.25分钟.
【变式3】(24-25高一上·全国·课后作业)人们早就发现了放射性物质的衰减现象.在考古工作中,常用的含量来确定有机物的年代.已知放射性物质的衰减服从指数规律:,其中t表示衰减的时间,表示放射性物质的原始质量,表示经衰减了t年后剩余的质量.为计算衰减的年代,通常给出该物质质量衰减一半的时间,称其为该物质的半衰期.的半衰期大约是5730年.人们又知道,放射性物质的衰减速度与其质量成正比.1950年,在伊拉克发现一根古巴比伦王国时期刻有汉谟拉比王朝字样的木炭,当时测定,其的衰减速度为4.09个/(),而新砍伐树木烧成的木炭中的衰减速度为6.68个/().请估算出汉谟拉比王朝所在年代.(参考数据:)
【答案】公元前2100年
【分析】首先由衰减规律得,从而,进一步由题意得,即,解指数方程即可进一步求解.
【详解】因为的半衰期大约是5730年,所以由衰减规律,得.
解得.因此的衰减规律服从指数型函数.
设发现汉谟拉比王朝字样的木炭时(1950年),该木炭已衰减了年.
因为放射性物质的衰减速度与其质量成正比,所以,
于是.
两边取以2为底的对数,得.
解得.
所以该木炭已衰减了约4055年,即汉谟拉比王朝大约存在于公元前2100年.
题型09数形结合的思想
【典例1】(23-24高二下·海南·期末)已知函数若关于的方程有两个不同的实根,则实数的取值范围是( )
A. B. C. D.
【答案】D
【分析】先进行变形,关于的方程有两个不同的实根,即关于的方程有两个不同的实根.即与有两个不同的交点.研究图像,数形结合可解.
【详解】,则关于的方程有两个不同的实根,即关于的方程有两个不同的实根.
即与有两个不同的交点.
令,,解得.
递增,递减,
则有极大值.,
则可画出的草图.与有两个不同的交点.
则实数的取值范围是.
故选:D.
【典例2】(23-24高二下·浙江杭州·期中)已知函数,若对于正数,直线与函数的图像恰好有个不同的交点,则 .
【答案】
【分析】由题意首先确定函数的性质,然后结合直线与圆的位置关系得到的表达式,最后裂项求和即可求得的值.
【详解】当时,,即,
表示以为圆心,为半径的圆在轴(含轴)的上半部分,
当时,,函数周期为4,
如图作出函数的图象,
因为与函数恰有个不同的交点,
根据图象知,直线与第个半圆相切,
第个半圆的圆心为,半径为,
故直线的斜率,
所以,
所以.
故答案为:.
【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解
【典例3】(23-24高二下·山东滨州·期末)设函数 若关于的方程有5个不相等的实数根,则实数的取值范围是 .
【答案】
【分析】令,代入方程解得或,则和共有5个不同的实数根.作出的图象,观察图象即可求出的取值范围.
【详解】令,则,即,即,解得或,则和共有5个不同的实数根.作出的图象,如图:
由图可知,,解得.
故答案为:.
【变式1】(23-24高一下·云南·期末)设,若关于的方程恰有5个不同实数解,则实数的取值范围是( )
A. B. C. D.
【答案】D
【分析】化方程为或,分析函数的性质,再利用数形结合法求出的范围.
【详解】方程化为,解得或,
函数在上单调递增,函数值集合为,在上单调递减,函数值集合为,
在上单调递增,函数值集合为,
在同一坐标系内作出直线与函数的图象,
显然直线与函数的图象有两个交点,
由关于的方程恰有5个不同实数解,则直线与函数的图象有3个交点,
此时,所以实数的取值范围是.
故选:B
【点睛】思路点睛:研究方程根的情况,可以通过转化,利用导数研究函数的单调性、最值等,借助数形结合思想分析问题,使问题的求解有一个清晰、直观的整体展现.
【变式2】(2024·天津河东·二模)已知函数,,若方程恰有2个不同的实数根,则实数的取值范围为 .
【答案】,,.
【分析】作出的图象,分、、、及五种情况,分别作出图象进行讨论,即可得答案.
【详解】依题意画出的图象如图所示:
因为函数,
所以,
当直线与相切时,
由,得,
,解得,
由图可知,①当时,函数的图象与的图象无交点,不满足题意;
②当时,函数的图象与的图象交于点,不满足题意;
③时,当经过函数图象上的点时,恰好经过函数图象上的点,
则要使方根恰有2个不同的实数根,
只需,即,故;
④当时,函数的图象与的图象有3个交点,不满足题意;
⑤当时,函数的图象与的图象有2个交点,满足题意.
综上,或.
所以的取值范围为:,,.
故答案为:,,.
【点睛】方法点睛:求解函数零点个数的常用方法:
(1) 直接法:令则方程实根的个数就是函数零点的个;
(2) 零点存在性定理法:判断函数在区间上是连续不断的曲线,且再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数;(3) 数形结合法:转化为两个函数的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,在一个区间上单调的函数在该区间内至多只有一个零点,在确定函数零点的唯一性时往往要利用函数的单调性,确定函数零点所在区间主要利用函数零点存在定理,有时可结合函数的图象辅助解题.
【变式3】(23-24高二下·湖南·期末)已知函数,且时,,则的取值范围为 .
【答案】
【分析】作出函数的图象,结合对数的运算性质求出,根据二次函数的对称性求出,再结合二次函数的性质即可得解.
【详解】作出函数的图象,如图所示,
因为时,,
由图可知,,
则,
即,所以,所以,
由函数关于对称,可得,
所以,
因为,所以,
即的取值范围为.
故答案为:.
【点睛】关键点点睛:作出函数的图象,结合对数的运算性质求出,根据二次函数的对称性求出,是解决本题的关键.
题型10分类讨论的思想
【典例1】(24-25高一上·上海·课堂例题)设(且),求的取值范围.
【答案】答案见解析
【分析】分类讨论和两种情况,结合指数函数的单调性和一元二次方程的解法即可求解
【详解】当时,由可得,
即,即,解得或;
当时,由可得,
即,即,解得.
综上所述,当时,的取值范围是;
当时,的取值范围是.
【典例2】(23-24高二下·山东青岛·期末)已知,,(且).
(1)若,,解不等式;
(2)若.
(ⅰ)当时,判断函数的奇偶性,并说明理由;
(ⅱ)当时,若的最小值为,求的值.
【答案】(1);
(2)(ⅰ)为偶函数,理由见解析;(ⅱ).
【分析】(1)时,由,可得,根据对数函数的单调性即可求解;
(2)(ⅰ)时,,判断其奇偶性即可;
(ⅱ)时,函数的定义域为,且,根据二次函数及对数函数的性质分类讨论即可求解.
【详解】(1)若,则,,
由,可得.
因为,所以,解得.
所以不等式的解集为.
(2)(ⅰ)若,则,
由,可得,即函数的定义域为,关于原点对称,
又,
所以函数为定义在上的偶函数.
(ⅱ)当时,,
令,解得,即函数的定义域为.
又
.
因为,所以,所以,
所以.
因为且,
所以当时,,
因为的最小值为,所以,解得.
当时,,不存在最小值,舍去.
综上所述,.
【变式1】(2024高三下·全国·专题练习)函数(,且)在上的最大值为13,求实数a的值.
【答案】3或
【分析】令,讨论或,求出t的取值范围,再利用二次函数的单调性即可求解.
【详解】∵
令,则,
则,其对称轴为.
该二次函数在上是增函数.
①若,由,得,
故当,即时,
,解得(舍去).
②若,由,可得,
故当,即时,
.
∴或(舍去).
综上可得或.
【变式2】(23-24高二下·山东青岛·阶段练习)已知函数.
(1)求函数的解析式;
(2)求函数的单调增区间.
【答案】(1)
(2)答案见解析
【分析】(1)将看成一个整体求解即可;
(2)利用复合函数的单调性求解即可.
【详解】(1),
所以.
(2),
所以是对称轴为,开口向上的二次函数,
且的解集为,
故在上单调递减,在单调递增.
当时,函数是增函数,故函数在上单调递减,在单调递增;
当时,函数是减函数,函数在上单调递增,在单调递减;
【变式3】(2024高三·全国·专题练习)已知函数 (且).
(1)当时,函数恒有意义,求实数的取值范围;
(2)是否存在这样的实数,使得函数在区间上为减函数,且最大值为?如果存在,试求出的值;如果不存在,请说明理由.
【答案】(1)
(2)不存在,理由见解析
【分析】(1)依题意可得在上恒成立,参变分离可得在上恒成立,令,,利用导数说明函数的单调性,即可求出的取值范围;
(2)由(1)同理可知,再分、两种情况讨论,结合二次函数的性质计算可得.
【详解】(1)当时,函数恒有意义,
所以在上恒成立,
即在上恒成立.
令,,
则,
所以在上单调递减,
所以,所以.
又且,所以.
(2)函数在区间上有意义,
则在上恒成立.
由(1)同理可知,,
又函数在区间上为减函数,并且最大值为.
当时,为减函数,
则且在上单调递增,
所以,即,故不存在这样的实数;
当时,为增函数,
则且在上单调递减,
所以,即,故不存在这样的实数.
综上,不存在这样的实数,使得函数在区间上为减函数,且最大值为.
题型11换元的思想
【典例1】(23-24高一下·云南曲靖·阶段练习)若函数在上是单调函数,且满足对任意,都有,则函数的零点所在的区间为( )
A. B. C. D.
【答案】D
【分析】设,根据,列出关于的方程,进而求得的值,得到的解析式,再用零点存在定理判断即可.
【详解】因为函数在上是单调函数,,
设,所以,
所以,
因为与在上单调递增,所以有唯一解,解得,
所以,
又,,
故的零点所在的区间为.
故选:B.
【典例2】(23-24高二下·宁夏银川·期末)已知函数是定义在上的奇函数.
(1)求的解析式并用定义证明的单调性;
(2)使得成立,求实数的取值范围.
【答案】(1),证明见解析
(2)
【分析】(1)根据奇函数(定义域为)的性质求出的值,再代入检验,最后根据单调性的定义证明函数的单调性;
(2)先将不等式化为,再利用换元法结合函数单调性求出的最小值即可得解.
【详解】(1)因为是定义在上的奇函数,
所以,解得,
则,
且,
所以为定义在上的奇函数,故,即.
是上的增函数,证明如下:
任取,且,
则
(2)∵在上恒成立,
又,当且仅当即时取等号,
∴的最小值为,∴.
【变式2】(23-24高三下·北京·阶段练习)已知函数(为实常数).
(1)若函数为奇函数,求的值;
(2)在(1)的条件下,对任意,不等式恒成立,求实数的最大值.
【答案】(1)
(2)1
【分析】(1)若函数为奇函数,由奇函数的性质可求得,并代入检验;
(2)对任意,不等式恒成立,化简不等式参变分离,构造新函数,利用换元法和对勾函数的单调性求出最值,代入得出实数u的最大值.
【详解】(1)由题意可知:的定义域为,
若函数为奇函数,则,解得,
此时,
则,
即,可知为奇函数,则符合题意,
综上所述:.
(2)由(1)可知,
由不等式,得,
原题意等价于,
因为,令,
则
又因为函数在单调递增,则,
可得,所以实数的最大值为1.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
