2.2 第4课时 二次函数y=ax2+bx+c的图象与性质 课件(共21张PPT) 2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 2.2 第4课时 二次函数y=ax2+bx+c的图象与性质 课件(共21张PPT) 2024-2025学年北师大版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-06 19:38:43 | ||
图片预览







文档简介
(共21张PPT)
北师版·九年级下册
第4课时 二次函数y=ax +bx+c的图象与性质
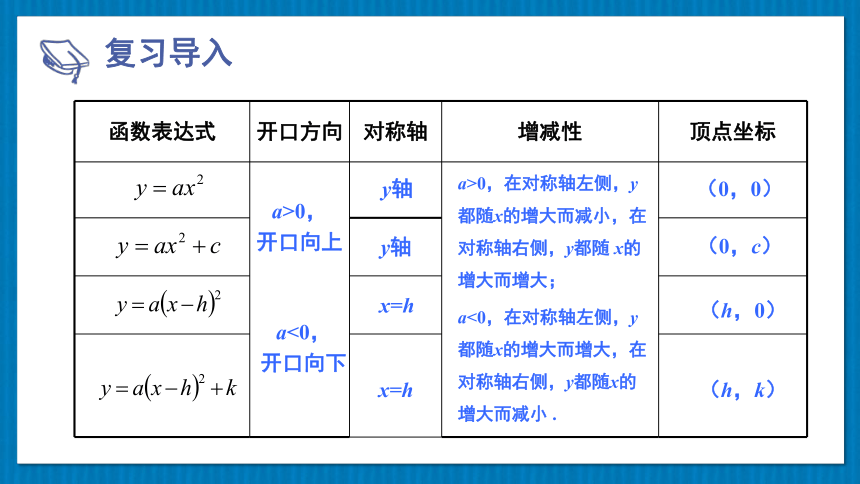
复习导入
函数表达式 开口方向 对称轴 增减性 顶点坐标
a<0,
开口向下
a>0,
开口向上
a<0,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随x的增大而减小 .
a>0,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大;
y轴
y轴
x=h
x=h
(0,0)
(0,c)
(h,0)
(h,k)
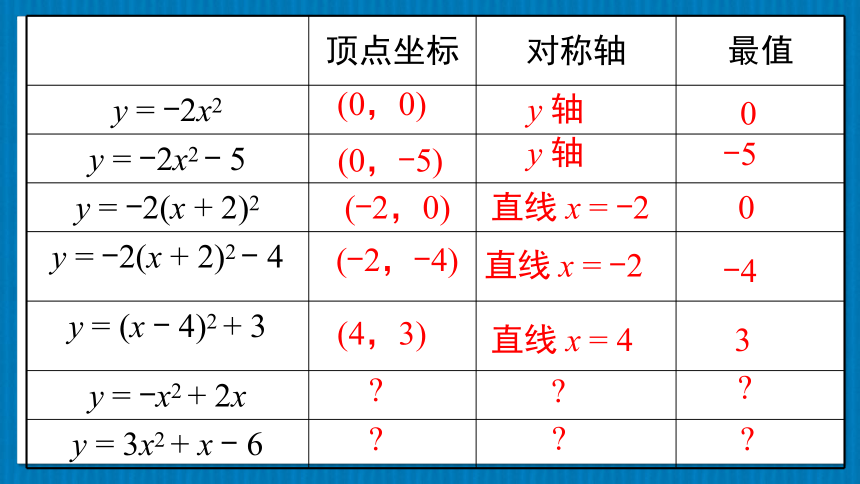
顶点坐标 对称轴 最值
y = -2x2
y = -2x2 - 5
y = -2(x + 2)2
y = -2(x + 2)2 - 4
y = (x - 4)2 + 3
y = -x2 + 2x
y = 3x2 + x - 6
(0,0)
y 轴
0
(0,-5)
y 轴
-5
(-2,0)
直线 x = -2
0
(-2,-4)
直线 x = -2
-4
(4,3)
直线 x = 4
3
二次函数 y = ax2 + bx + c 的图象和性质
1
猜想:通过组合平移 y = ax (a≠0) 的图像能否得到
y = ax + bx + c (a≠0) 的图像?
y = ax
通过上下左右平移
y = a(x h)2+k
y = ax +bx+c
是否有关系?
相互转化
(1) x2 12x + 36 = (x____)2;
填一填
(2) x2 12x = (x____)2 ____.
6
36
6
探究新知
我们已经认识了形如y=a(x-h)2+k的二次函数的图象和性质,你能研究二次函数y=2x2-4x+5的图象和性质吗
化成y=a(x-h)2+k的形式.
合作探究
问题1 怎样将 y=2x - 4x + 5化成 y = a(x h)2 + k 的形式?
想一想:配方的方法及步骤是什么?
y = 2x - 4x + 5
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的解析式通常称为顶点式.
= 2(x - 2x) + 5
= 2(x - 2x + 1 - 1 ) + 5
= 2(x - 1) + 3
探究新知
例1 求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
解: y = 2x2-8x+7
= 2(x2-4x)+7
= 2(x2-4x+4)-8+7
= 2(x-2)2-1
∴ 对称轴是x=2,顶点坐标为(2,-1)
提取二次项系数
配方
顶点式
做一做
确定下列二次函数图象的对称轴和顶点坐标:
(1)y=3x2-6x+7;
(2)y=2x2-12x+8;
= 3(x2-2x)+7
= 3(x2-2x+1)-3+7
= 3(x-1)2+4
对称轴是x=1,顶点坐标为(1,4)
= 2(x2-6x)+8
= 2(x2-6x+9)-18+8
= 2(x-3)2-10
对称轴是x=3,
顶点坐标为(3,-10)
例2 求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
y = ax2+bx+c
解:把二次函数y=ax2+bx+c的右边配方,得
∴对称轴是 ,顶点坐标为
y
O
x
(a>0)
y
O
x
(a<0)
二次函数y=ax2+bx+c的图象:
最小值
最大值
如果 a<0,当 x< 时,y 随 x 的增大而增大;
当x> 时,y 随 x 的增大而减小.
如果 a>0,当 x< 时,y 随 x 的增大而减小;
当 x> 时,y 随 x 的增大而增大.
(1)
(2)
x
y
O
x
y
O
归纳总结
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
做一做
如图,桥梁的两条钢缆具有相同的抛物线形状,而且左右两条抛物线关于y轴对称.按照图中的直角坐标系,左面的一条抛物线可以用 表示.
(1)钢缆的最低点到桥面的距离是多少
(2)两条钢缆最低点之间的距离是多少
y/m
x/m
桥面 -5 O 5
10
解:
顶点坐标
顶点坐标
∴钢缆的最低点到桥面的距离是1m
两条钢缆最低点之间的距离是|-20|×2=40m
y/m
x/m
桥面 -5 O 5
10
1.用配方法确定下列函数图象的对称轴和顶点坐标:
(1)y=2x2-12x+3; (2)y=-5x2+80x-319;
= 2(x2-6x)+3
= 2(x2-6x+9)-18+3
= 2(x-3)2-15
对称轴为x=3,
顶点为(3,-15).
= -5(x2-16x)-319
= -5(x2-16x+64)+320-319
= -5(x-8)2+1
对称轴为x=8,
顶点为(8,1).
1.用配方法确定下列函数图象的对称轴和顶点坐标:
(3)y= ; (4)y=-3(x+3)(x+9).
= 2x2-5x+2
对称轴为x= ,顶点为 .
= -6x2+9x+6
对称轴为x= ,顶点为 .
2.已知二次函数 y = ax2+bx+c 的 x、y 的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
A. y轴 B. 直线 x=
C. 直线 x=2 D. 直线 x=
则该二次函数图象的对称轴为( )
D
1
3.二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c图象的对称轴为x= , x=2对应的函数值y= .
-8
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
课堂小结
课后作业
课后练习+习题2.5
1、2、3、4
课后练习
1.确定下列抛物线的开口方向、对称轴及顶点坐标.
(1)y=-3x2+12x-3; (2)y=4x2-24x+26;
(3)y=2x2+8x-6; (4)y= x2-2x-1.
开口向上,
对称轴为x=3,
顶点为(3, - 10).
开口向下,
对称轴为x=2,
顶点为(2,9).
开口向上,
对称轴为x=-2
顶点为( - 2, - 14).
开口向上,
对称轴为x=2,
顶点为(2, - 3).
北师版·九年级下册
第4课时 二次函数y=ax +bx+c的图象与性质
复习导入
函数表达式 开口方向 对称轴 增减性 顶点坐标
a<0,
开口向下
a>0,
开口向上
a<0,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随x的增大而减小 .
a>0,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大;
y轴
y轴
x=h
x=h
(0,0)
(0,c)
(h,0)
(h,k)
顶点坐标 对称轴 最值
y = -2x2
y = -2x2 - 5
y = -2(x + 2)2
y = -2(x + 2)2 - 4
y = (x - 4)2 + 3
y = -x2 + 2x
y = 3x2 + x - 6
(0,0)
y 轴
0
(0,-5)
y 轴
-5
(-2,0)
直线 x = -2
0
(-2,-4)
直线 x = -2
-4
(4,3)
直线 x = 4
3
二次函数 y = ax2 + bx + c 的图象和性质
1
猜想:通过组合平移 y = ax (a≠0) 的图像能否得到
y = ax + bx + c (a≠0) 的图像?
y = ax
通过上下左右平移
y = a(x h)2+k
y = ax +bx+c
是否有关系?
相互转化
(1) x2 12x + 36 = (x____)2;
填一填
(2) x2 12x = (x____)2 ____.
6
36
6
探究新知
我们已经认识了形如y=a(x-h)2+k的二次函数的图象和性质,你能研究二次函数y=2x2-4x+5的图象和性质吗
化成y=a(x-h)2+k的形式.
合作探究
问题1 怎样将 y=2x - 4x + 5化成 y = a(x h)2 + k 的形式?
想一想:配方的方法及步骤是什么?
y = 2x - 4x + 5
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的解析式通常称为顶点式.
= 2(x - 2x) + 5
= 2(x - 2x + 1 - 1 ) + 5
= 2(x - 1) + 3
探究新知
例1 求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
解: y = 2x2-8x+7
= 2(x2-4x)+7
= 2(x2-4x+4)-8+7
= 2(x-2)2-1
∴ 对称轴是x=2,顶点坐标为(2,-1)
提取二次项系数
配方
顶点式
做一做
确定下列二次函数图象的对称轴和顶点坐标:
(1)y=3x2-6x+7;
(2)y=2x2-12x+8;
= 3(x2-2x)+7
= 3(x2-2x+1)-3+7
= 3(x-1)2+4
对称轴是x=1,顶点坐标为(1,4)
= 2(x2-6x)+8
= 2(x2-6x+9)-18+8
= 2(x-3)2-10
对称轴是x=3,
顶点坐标为(3,-10)
例2 求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
y = ax2+bx+c
解:把二次函数y=ax2+bx+c的右边配方,得
∴对称轴是 ,顶点坐标为
y
O
x
(a>0)
y
O
x
(a<0)
二次函数y=ax2+bx+c的图象:
最小值
最大值
如果 a<0,当 x< 时,y 随 x 的增大而增大;
当x> 时,y 随 x 的增大而减小.
如果 a>0,当 x< 时,y 随 x 的增大而减小;
当 x> 时,y 随 x 的增大而增大.
(1)
(2)
x
y
O
x
y
O
归纳总结
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
做一做
如图,桥梁的两条钢缆具有相同的抛物线形状,而且左右两条抛物线关于y轴对称.按照图中的直角坐标系,左面的一条抛物线可以用 表示.
(1)钢缆的最低点到桥面的距离是多少
(2)两条钢缆最低点之间的距离是多少
y/m
x/m
桥面 -5 O 5
10
解:
顶点坐标
顶点坐标
∴钢缆的最低点到桥面的距离是1m
两条钢缆最低点之间的距离是|-20|×2=40m
y/m
x/m
桥面 -5 O 5
10
1.用配方法确定下列函数图象的对称轴和顶点坐标:
(1)y=2x2-12x+3; (2)y=-5x2+80x-319;
= 2(x2-6x)+3
= 2(x2-6x+9)-18+3
= 2(x-3)2-15
对称轴为x=3,
顶点为(3,-15).
= -5(x2-16x)-319
= -5(x2-16x+64)+320-319
= -5(x-8)2+1
对称轴为x=8,
顶点为(8,1).
1.用配方法确定下列函数图象的对称轴和顶点坐标:
(3)y= ; (4)y=-3(x+3)(x+9).
= 2x2-5x+2
对称轴为x= ,顶点为 .
= -6x2+9x+6
对称轴为x= ,顶点为 .
2.已知二次函数 y = ax2+bx+c 的 x、y 的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
A. y轴 B. 直线 x=
C. 直线 x=2 D. 直线 x=
则该二次函数图象的对称轴为( )
D
1
3.二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c图象的对称轴为x= , x=2对应的函数值y= .
-8
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
课堂小结
课后作业
课后练习+习题2.5
1、2、3、4
课后练习
1.确定下列抛物线的开口方向、对称轴及顶点坐标.
(1)y=-3x2+12x-3; (2)y=4x2-24x+26;
(3)y=2x2+8x-6; (4)y= x2-2x-1.
开口向上,
对称轴为x=3,
顶点为(3, - 10).
开口向下,
对称轴为x=2,
顶点为(2,9).
开口向上,
对称轴为x=-2
顶点为( - 2, - 14).
开口向上,
对称轴为x=2,
顶点为(2, - 3).
