江苏省苏州高新区实验初级中学2024-2025学年九年级上学期数学12月月考试题(图片版,无答案)
文档属性
| 名称 | 江苏省苏州高新区实验初级中学2024-2025学年九年级上学期数学12月月考试题(图片版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-06 00:00:00 | ||
图片预览

文档简介
2024~2025学年第一学期初三数学现场作业2024.12
一、进择题(本大题共有8小,每小趣3分,共24分在年小题给出的四个选项中,只有一项悬
符合照目琴求的)
1.i
知⊙0的半径为5cm,P0=3cm,则点P与⊙0的位凰关系是(A)
A.点P在圆外B.点P在圆上
C.点P在圆内
D.无法确定
2.已知二次函数的解析式为y=-x+2:,下列关于函数图做的说法正确的是(▲)
对称轴是直线x=-】B.图像经过原点(。开口向上D.图像有锻低点
3.一个不透明的袋子里装有3个红球和4个黄球,它们除颜色外其余都相同.从袋中任意摸出一
个球是红球的概率为(▲)
A
c月
4.如图,A、B、C、D都是⊙O上的点,若CD=BD,∠AOC=108°,则∠AOD=(A)
A.140°
B.144°
C.146°
D.150°
5.下列说法正确的是(▲)
·三个点可以确定一个圆
B.三角形的外心是这个三角形三条角平分线的交点
G,过弦的中点的直线必过圆心D.垂直于弦的直径平分这条弦并且平分弦所对的两条弧
6.已知点(-1,),(42).(-3,乃)都在函数y=m2-4m+c(a<0)上,则(▲)
A.y3C.为D,为7.如图,在RtABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆的半径为(A)
A.1
B.2
c是
D骨
8.如图,平面直角坐标系xOy中,点A的坐标是一3.4),点B是⊙A上一点,⊙A的半径为2,将0B
绕O点烦时针方向旋转90得OC,连接AC,则线段AC的斑小值为(▲)
A.5N2-2
B.3N2-1
c.5
D.6
第4题
第7题
第8题
第10题
二、填空题(本大题共有8小题,年小题3分,共24分不语写出解答过程放把:蒸接然写在
容别纸相碑位殿上)
9.某校随机抽查6名学生每天完成谀后作业的时间(单位:分钟)是:54,62,746,90,97,则
这组数据的中位数是▲
10。如图是一个可以自由转动的转盘,如果转动一次转盘,`转盘中阴影部分的扇形的圆心角度数为
120°.则停止后指针扮向阴影部分的概率是▲一·
11.⊙0的直径为17cm,若圆心0与直线1的距离为7.5cm,则1与⊙0的位贸关系是▲(填
"相交、“相切或“相离”).
12.抛物线y=x2的图像向右平移1个单位长度,再向上平移3个单位长度,所得抛物线的丧达式
是▲
13.若一条弦把圆分成1:5两部分,则这条弦所对的圆周角为▲
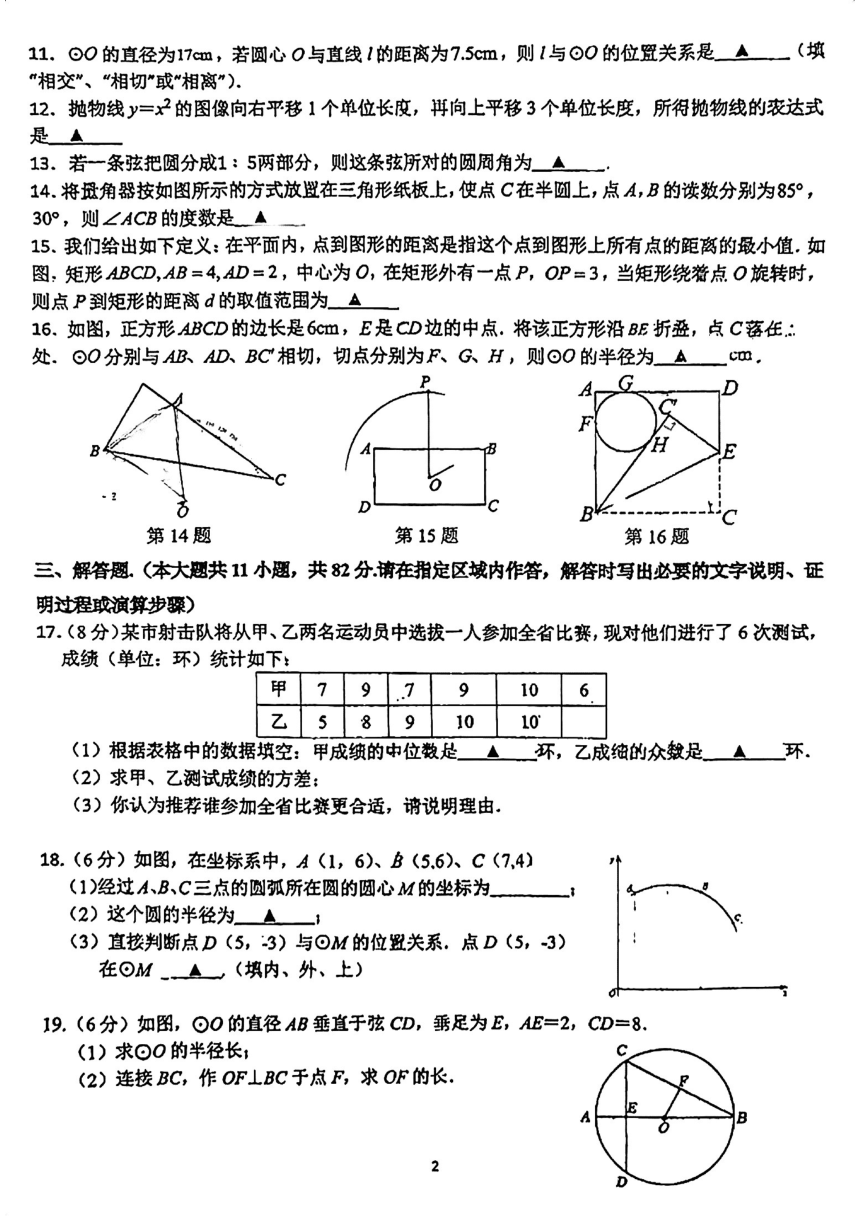
14.将斑角器按如图所示的方式放遐在三角形纸板上,使点C在半圆上,点A,B的泼数分别为85°,
30°,则∠ACB的度数是▲
15.我们给出如下定义:在平而内,点到图形的距离是指这个点到图形上所有点的距离的最小值.如
图,矩形ABCD,AB=4,AD=2,中心为O,在矩形外有一点P,OP=3,当矩形绕着点O旋转时,
则点P到矩形的距离d的取值范围为△
16.如图,正方形ABCD的边长是6cm,E是CD边的中点.将该正方形沿BE折叠,点C落任:
处.⊙O分别与ABAD,BC相切,切点分别为F、GH,则⊙O的半径为Am,
第14题
第15题
第16题
三、解答题。(本大思共11小题,共82分请在指定区域内作答,解答时写出必要的文字说明、证
明过程或演算步骤)
17.(8分)某市射击队将从甲、乙两名运动员中选拔一人参加全省比赛,现对他们进行了6次测试,
成绩(单位:环)统计如下
甲
7
9
.7
9
10
6
乙
中
9
10
10
(1)根据表格中的数据填空:甲成统的中位数是
▲环,乙成细的众毅是▲环
(2)求甲、乙测试成绩的方差:
(3)你认为推荐谁参加全省比篓更合适,谛说明理由.
18.(6分)如图,在坐标系中,A(1,6)、B(5.6)、C(7,4)
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
(2)这个圆的半径为▲一1
(3)直按判断点D(5,3)与⊙M的位关系。点D(5,3)
在⊙M-▲一(填内、外、上)
I9.(6分)如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙0的半径长1
(2)连接BC,作OF⊥BC于点F,求OF的长.
一、进择题(本大题共有8小,每小趣3分,共24分在年小题给出的四个选项中,只有一项悬
符合照目琴求的)
1.i
知⊙0的半径为5cm,P0=3cm,则点P与⊙0的位凰关系是(A)
A.点P在圆外B.点P在圆上
C.点P在圆内
D.无法确定
2.已知二次函数的解析式为y=-x+2:,下列关于函数图做的说法正确的是(▲)
对称轴是直线x=-】B.图像经过原点(。开口向上D.图像有锻低点
3.一个不透明的袋子里装有3个红球和4个黄球,它们除颜色外其余都相同.从袋中任意摸出一
个球是红球的概率为(▲)
A
c月
4.如图,A、B、C、D都是⊙O上的点,若CD=BD,∠AOC=108°,则∠AOD=(A)
A.140°
B.144°
C.146°
D.150°
5.下列说法正确的是(▲)
·三个点可以确定一个圆
B.三角形的外心是这个三角形三条角平分线的交点
G,过弦的中点的直线必过圆心D.垂直于弦的直径平分这条弦并且平分弦所对的两条弧
6.已知点(-1,),(42).(-3,乃)都在函数y=m2-4m+c(a<0)上,则(▲)
A.y3
A.1
B.2
c是
D骨
8.如图,平面直角坐标系xOy中,点A的坐标是一3.4),点B是⊙A上一点,⊙A的半径为2,将0B
绕O点烦时针方向旋转90得OC,连接AC,则线段AC的斑小值为(▲)
A.5N2-2
B.3N2-1
c.5
D.6
第4题
第7题
第8题
第10题
二、填空题(本大题共有8小题,年小题3分,共24分不语写出解答过程放把:蒸接然写在
容别纸相碑位殿上)
9.某校随机抽查6名学生每天完成谀后作业的时间(单位:分钟)是:54,62,746,90,97,则
这组数据的中位数是▲
10。如图是一个可以自由转动的转盘,如果转动一次转盘,`转盘中阴影部分的扇形的圆心角度数为
120°.则停止后指针扮向阴影部分的概率是▲一·
11.⊙0的直径为17cm,若圆心0与直线1的距离为7.5cm,则1与⊙0的位贸关系是▲(填
"相交、“相切或“相离”).
12.抛物线y=x2的图像向右平移1个单位长度,再向上平移3个单位长度,所得抛物线的丧达式
是▲
13.若一条弦把圆分成1:5两部分,则这条弦所对的圆周角为▲
14.将斑角器按如图所示的方式放遐在三角形纸板上,使点C在半圆上,点A,B的泼数分别为85°,
30°,则∠ACB的度数是▲
15.我们给出如下定义:在平而内,点到图形的距离是指这个点到图形上所有点的距离的最小值.如
图,矩形ABCD,AB=4,AD=2,中心为O,在矩形外有一点P,OP=3,当矩形绕着点O旋转时,
则点P到矩形的距离d的取值范围为△
16.如图,正方形ABCD的边长是6cm,E是CD边的中点.将该正方形沿BE折叠,点C落任:
处.⊙O分别与ABAD,BC相切,切点分别为F、GH,则⊙O的半径为Am,
第14题
第15题
第16题
三、解答题。(本大思共11小题,共82分请在指定区域内作答,解答时写出必要的文字说明、证
明过程或演算步骤)
17.(8分)某市射击队将从甲、乙两名运动员中选拔一人参加全省比赛,现对他们进行了6次测试,
成绩(单位:环)统计如下
甲
7
9
.7
9
10
6
乙
中
9
10
10
(1)根据表格中的数据填空:甲成统的中位数是
▲环,乙成细的众毅是▲环
(2)求甲、乙测试成绩的方差:
(3)你认为推荐谁参加全省比篓更合适,谛说明理由.
18.(6分)如图,在坐标系中,A(1,6)、B(5.6)、C(7,4)
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
(2)这个圆的半径为▲一1
(3)直按判断点D(5,3)与⊙M的位关系。点D(5,3)
在⊙M-▲一(填内、外、上)
I9.(6分)如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙0的半径长1
(2)连接BC,作OF⊥BC于点F,求OF的长.
同课章节目录
