九年级上册北师大版1.1 菱形的判定 课件(共27张PPT)
文档属性
| 名称 | 九年级上册北师大版1.1 菱形的判定 课件(共27张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 12:07:26 | ||
图片预览




文档简介
(共27张PPT)
有趣的菱形
有趣的菱形
有趣的菱形
菱形的判定
初中数学 九年级上册 北京师范大学出版社
学习目标
1.经历菱形判定定理的探索过程,发展学生的推理能力、几何直观和空间观念.
2.会用菱形的判定方法进行相关的计算和证明,发展学生的应用意识.
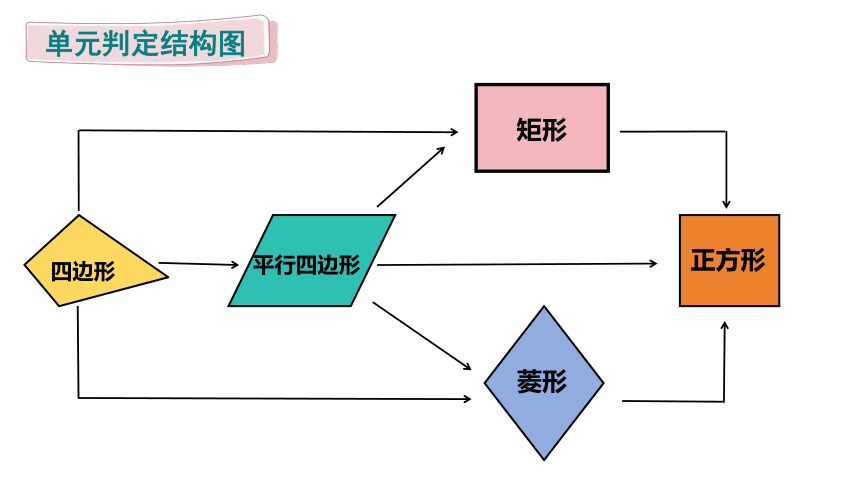
四边形
平行四边形
矩形
菱形
正方形
单元判定结构图
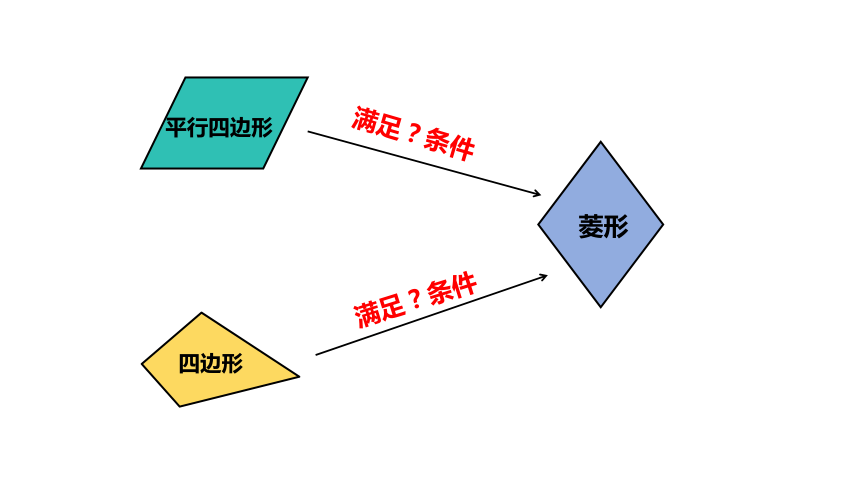
四边形
平行四边形
菱形
满足?条件
满足?条件
探究新知
小明想知道家里一幅风景画的相框是否是菱形,他该怎么做?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
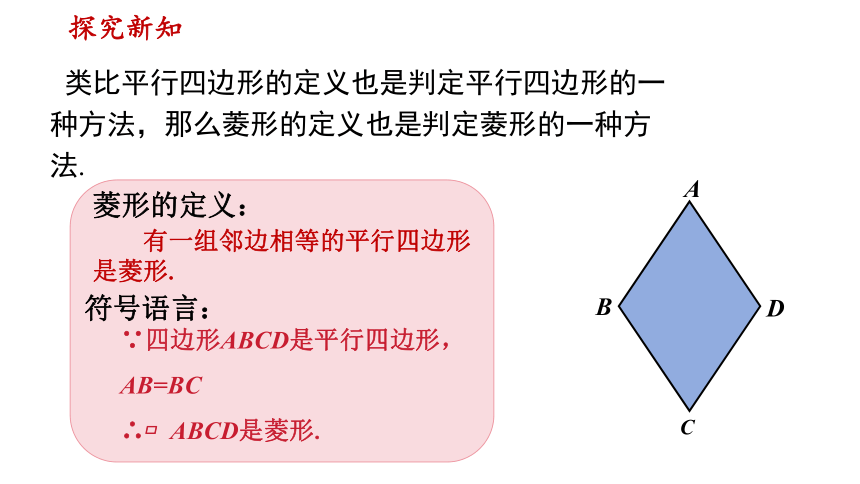
类比平行四边形的定义也是判定平行四边形的一种方法,那么菱形的定义也是判定菱形的一种方法.
探究新知
A
B
C
D
菱形的定义:
有一组邻边相等的平行四边形是菱形.
符号语言:
∵四边形ABCD是平行四边形,
AB=BC
∴ ABCD是菱形.
探究新知
探究新知
如图所示,小唯在一长一短两根木棍的中点处固定一个小钉,以小木棍作为四边形的对角线,四周围上一根橡皮筋,转动小木棍,探究什么时候橡皮筋所构成的四边形为菱形.
我们发现当两根木棍互相垂直时,构成的四边形为菱形,你能证明它吗?
证明:
四边形ABCD是平行四边形,AC⊥BD.
四边形ABCD是菱形.
已知:
求证:
证明猜想
对角线互相垂直的平行四边形是菱形
∵四边形 ABCD 是平行四边形
∴OA = OC
又∵AC ⊥ BD
∴BD 是线段 AC 的垂直平分线
∴BA = BC
∴四边形 ABCD 是菱形(菱形的定义)
归纳总结
对角线互相垂直的平行四边形是菱形.
在 ABCD中,
∵AC⊥BD
∴四边形ABCD是菱形
符号语言:
菱形的判定定理:
任务一:菱形判定定理(指向目标1)
四边形
平行四边形
菱形
一组邻边相等
对角线互相垂直
满足?条件
已知线段 AC,你能用尺规作图的方法作一个菱形 ABCD,使 AC 为菱形的一条对角线吗?你有几种方法?
如图,分别以 A,C 为圆心,以大于 AC 的长为半径作弧,两条弧分别交于 B、D,依次连接 A,B,C,D,四边形 ABCD 看上去是菱形.
再探新知
猜想:四条边相等的四边形是菱形.
已知:
求证:
证明猜想
四条边相等的四边形是菱形
如图,在四边形ABCD中,AB=BC=CD=DA.
四边形ABCD是菱形.
证明:∵AB = CD,BC = DA,
∴四边形 ABCD 是平行四边形,
又∵AB = BC,
∴四边形 ABCD 是菱形(菱形的定义)
A
B
C
D
菱形的判定定理:
符号语言:
归纳总结
四条边相等的四边形是菱形.
在四边形ABCD中,
∵ AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
任务一:菱形的判定定理(指向目标1)
×
√
×
√
下列判定相框为菱形的方法中哪些正确?为什么?
(检测目标1)
(1)一组邻边相等的四边形是菱形; ( )
(2)四条边都相等的四边形是菱形; ( )
(3)对角线互相垂直的四边形是菱形; ( )
(4)对角线互相平分且垂直的四边形是菱形; ( )
跟踪训练1
A等级:全部正确
B等级:3个正确.
C等级:其他.
评价标准
跟踪训练2
你能用折纸等办法得到一个菱形吗?动手试一试!
先将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,将纸展开,就得到了一个菱形.你能说说这是什么道理吗?
A等级:推理合理.
B等级:推理欠合理.
C等级:其它.
评价标准
任务二:菱形判定定理的应用(指向目标2)
例 2 已知:如图,在 □ ABCD 中,对角线 AC 与 BD 相交于点 O,AB = ,OA = 2,OB = 1.
求证:□ ABCD 是菱形.
证明:在△AOB 中,
∵AB = ,OA = 2,OB = 1,
∴AB2 = AO2 + OB2.
∴△AOB 是直角三角形,∠AOB 是直角.
∴AC ⊥ BD.
∴□ ABCD 是菱形(对角线垂直的平行四边形是菱形).
跟踪训练3
已知:如图,在□ABCD 中,对角线 AC 的垂直平分线分别与 AD,AC,BC 相交于点 E,O,F. 求证:四边形 AFCE 是菱形.
证明:在□ABCD 中,AD∥BC,即 AE∥FC.
又∵EF为 AC 的垂直平分线,
∴AC⊥EF,AO = OC,
即∠AOE=∠COF=90°,∠EAO=∠FCO.
∴△FOC≌△EOA,即AE=FC.
∴四边形 AFCE 为平行四边形.
又∵AC⊥EF,∴四边形 AFCE 是菱形.
A等级:推理合理.
B等级:推理欠合理.
C等级:其它.
评价标准
知识驿站
四边形
平行四边形
菱形
一组邻边相等
四条边相等
对角线互相垂直
当堂检测
1.如图,在 ABCD中,AC、BD相交于点O,要使 ABCD是菱形,添加下列条件能判定 ABCD是菱形的是( )(检测目标1)
A.AD=BC B.AB=DC
C.AC=BD D.AC⊥BD
第1、2每题30分,第3题40分
A等级:100分.
B等级:60分-80分.
C等级:60分以下.
评价标准
D
当堂检测
2.如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是
( )(检测目标1)
A.24 B.28
C.32 D.36
A
当堂检测
3.(检测目标2)如图,已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,继续分别以点B,D为圆心,线段AB长为半径画弧交于点C,连接BC,CD,则所得四边形ABCD为菱形,判定依据是: .
四条边相等的四边形是菱形
课堂总评
对标 评价标准 等级(A等级;B等级;C等级) 对应知识短板
目标1 1.通过活动,能够探索并掌握菱形的判定定理. 2.完成跟踪训练1,2,并做出评价.
目标2 1.会用菱形的判定定理解决实际问题. 2.完成跟踪训练3,并做出评价.
合计
分层作业
拓展作业:
A等级:本节同步练习册4-6题
B等级:本节同步练习册1-4题
请同学们用量角器、一条较长的绳子,检验相框是否是菱形.
结束寄语
用数学的思维思考现实世界
用数学的语言表达现实世界
用数学的眼光观察现实世界
有趣的菱形
有趣的菱形
有趣的菱形
菱形的判定
初中数学 九年级上册 北京师范大学出版社
学习目标
1.经历菱形判定定理的探索过程,发展学生的推理能力、几何直观和空间观念.
2.会用菱形的判定方法进行相关的计算和证明,发展学生的应用意识.
四边形
平行四边形
矩形
菱形
正方形
单元判定结构图
四边形
平行四边形
菱形
满足?条件
满足?条件
探究新知
小明想知道家里一幅风景画的相框是否是菱形,他该怎么做?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
类比平行四边形的定义也是判定平行四边形的一种方法,那么菱形的定义也是判定菱形的一种方法.
探究新知
A
B
C
D
菱形的定义:
有一组邻边相等的平行四边形是菱形.
符号语言:
∵四边形ABCD是平行四边形,
AB=BC
∴ ABCD是菱形.
探究新知
探究新知
如图所示,小唯在一长一短两根木棍的中点处固定一个小钉,以小木棍作为四边形的对角线,四周围上一根橡皮筋,转动小木棍,探究什么时候橡皮筋所构成的四边形为菱形.
我们发现当两根木棍互相垂直时,构成的四边形为菱形,你能证明它吗?
证明:
四边形ABCD是平行四边形,AC⊥BD.
四边形ABCD是菱形.
已知:
求证:
证明猜想
对角线互相垂直的平行四边形是菱形
∵四边形 ABCD 是平行四边形
∴OA = OC
又∵AC ⊥ BD
∴BD 是线段 AC 的垂直平分线
∴BA = BC
∴四边形 ABCD 是菱形(菱形的定义)
归纳总结
对角线互相垂直的平行四边形是菱形.
在 ABCD中,
∵AC⊥BD
∴四边形ABCD是菱形
符号语言:
菱形的判定定理:
任务一:菱形判定定理(指向目标1)
四边形
平行四边形
菱形
一组邻边相等
对角线互相垂直
满足?条件
已知线段 AC,你能用尺规作图的方法作一个菱形 ABCD,使 AC 为菱形的一条对角线吗?你有几种方法?
如图,分别以 A,C 为圆心,以大于 AC 的长为半径作弧,两条弧分别交于 B、D,依次连接 A,B,C,D,四边形 ABCD 看上去是菱形.
再探新知
猜想:四条边相等的四边形是菱形.
已知:
求证:
证明猜想
四条边相等的四边形是菱形
如图,在四边形ABCD中,AB=BC=CD=DA.
四边形ABCD是菱形.
证明:∵AB = CD,BC = DA,
∴四边形 ABCD 是平行四边形,
又∵AB = BC,
∴四边形 ABCD 是菱形(菱形的定义)
A
B
C
D
菱形的判定定理:
符号语言:
归纳总结
四条边相等的四边形是菱形.
在四边形ABCD中,
∵ AB=BC=CD=DA
∴四边形ABCD是菱形.
A
B
C
D
任务一:菱形的判定定理(指向目标1)
×
√
×
√
下列判定相框为菱形的方法中哪些正确?为什么?
(检测目标1)
(1)一组邻边相等的四边形是菱形; ( )
(2)四条边都相等的四边形是菱形; ( )
(3)对角线互相垂直的四边形是菱形; ( )
(4)对角线互相平分且垂直的四边形是菱形; ( )
跟踪训练1
A等级:全部正确
B等级:3个正确.
C等级:其他.
评价标准
跟踪训练2
你能用折纸等办法得到一个菱形吗?动手试一试!
先将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,将纸展开,就得到了一个菱形.你能说说这是什么道理吗?
A等级:推理合理.
B等级:推理欠合理.
C等级:其它.
评价标准
任务二:菱形判定定理的应用(指向目标2)
例 2 已知:如图,在 □ ABCD 中,对角线 AC 与 BD 相交于点 O,AB = ,OA = 2,OB = 1.
求证:□ ABCD 是菱形.
证明:在△AOB 中,
∵AB = ,OA = 2,OB = 1,
∴AB2 = AO2 + OB2.
∴△AOB 是直角三角形,∠AOB 是直角.
∴AC ⊥ BD.
∴□ ABCD 是菱形(对角线垂直的平行四边形是菱形).
跟踪训练3
已知:如图,在□ABCD 中,对角线 AC 的垂直平分线分别与 AD,AC,BC 相交于点 E,O,F. 求证:四边形 AFCE 是菱形.
证明:在□ABCD 中,AD∥BC,即 AE∥FC.
又∵EF为 AC 的垂直平分线,
∴AC⊥EF,AO = OC,
即∠AOE=∠COF=90°,∠EAO=∠FCO.
∴△FOC≌△EOA,即AE=FC.
∴四边形 AFCE 为平行四边形.
又∵AC⊥EF,∴四边形 AFCE 是菱形.
A等级:推理合理.
B等级:推理欠合理.
C等级:其它.
评价标准
知识驿站
四边形
平行四边形
菱形
一组邻边相等
四条边相等
对角线互相垂直
当堂检测
1.如图,在 ABCD中,AC、BD相交于点O,要使 ABCD是菱形,添加下列条件能判定 ABCD是菱形的是( )(检测目标1)
A.AD=BC B.AB=DC
C.AC=BD D.AC⊥BD
第1、2每题30分,第3题40分
A等级:100分.
B等级:60分-80分.
C等级:60分以下.
评价标准
D
当堂检测
2.如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是
( )(检测目标1)
A.24 B.28
C.32 D.36
A
当堂检测
3.(检测目标2)如图,已知∠A,以点A为圆心,恰当长为半径画弧,分别交AE,AF于点B,D,继续分别以点B,D为圆心,线段AB长为半径画弧交于点C,连接BC,CD,则所得四边形ABCD为菱形,判定依据是: .
四条边相等的四边形是菱形
课堂总评
对标 评价标准 等级(A等级;B等级;C等级) 对应知识短板
目标1 1.通过活动,能够探索并掌握菱形的判定定理. 2.完成跟踪训练1,2,并做出评价.
目标2 1.会用菱形的判定定理解决实际问题. 2.完成跟踪训练3,并做出评价.
合计
分层作业
拓展作业:
A等级:本节同步练习册4-6题
B等级:本节同步练习册1-4题
请同学们用量角器、一条较长的绳子,检验相框是否是菱形.
结束寄语
用数学的思维思考现实世界
用数学的语言表达现实世界
用数学的眼光观察现实世界
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
