青岛版数学八年级下册 6.1平行四边形及其性质 课件(共24张PPT)
文档属性
| 名称 | 青岛版数学八年级下册 6.1平行四边形及其性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 13:21:23 | ||
图片预览








文档简介
(共24张PPT)
情景导入
6.1.1 平行四边形及其性质
青岛版 数学 八年级 下册
1、理解平行四边形的概念。
2、掌握平行四边形的性质,并灵活运用平行四边形的性质解决问题。
3、经历“猜想-验证-结论-证明”的过程,发展思维能力,培养探究意识。
用两个全等的三角形纸片拼出形状不同的四边形,其中哪些是平行四边形?为什么?
活动一
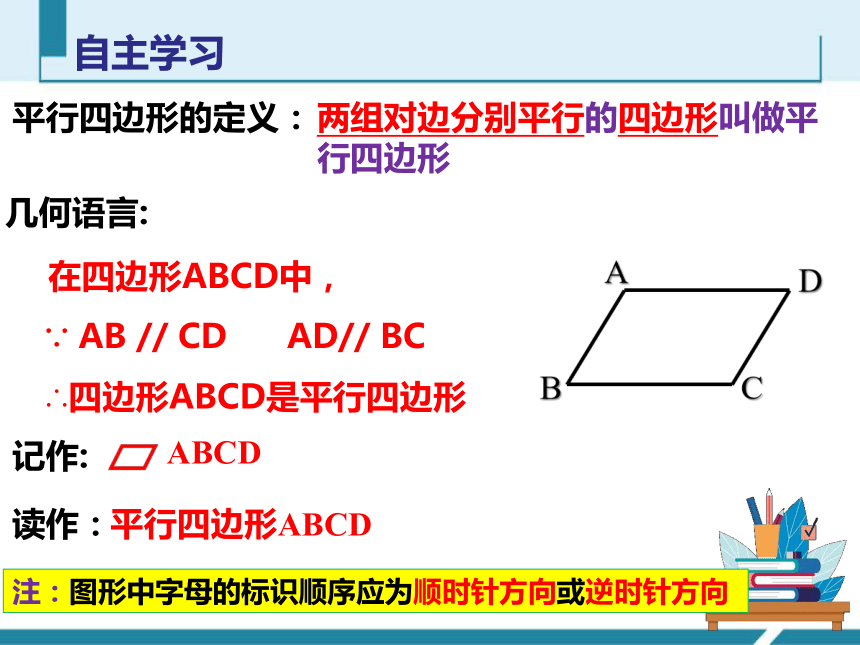
平行四边形的定义:
读作:
记作:
几何语言:
自主学习
在四边形ABCD中,
∵ AB // CD AD// BC
∴四边形ABCD是平行四边形
平行四边形ABCD
注:图形中字母的标识顺序应为顺时针方向或逆时针方向
两组对边分别平行的四边形叫做平行四边形
ABCD
对边: ;
对角: ;
对角线: 。
AB与CD,AD与BC
∠A与∠C,∠B与∠D
AC和BD
A
D
C
B
自主学习
不相邻的两个顶点连成的线段叫做对角线
探索之旅
第一站
猜想
1.平行四边形的对边具有哪些性质?
2.平行四边形的对角具有哪些性质?
能否验证你的猜想呢?
探究新知
第一站
第二站
验证
小组分工合作: 选择学具验证,并记录总结,代表汇报。
活动二
第一站
第二站
第三站
结论
1、平行四边形的两组对边分别相等。
2、平行四边形的两组对角分别相等。
探究新知
第一站
第二站
第三站
第四站
已知: ABCD
求证:①AB=CD,BC=DA;
②∠B=∠D,∠A=∠C.
A
B
C
D
活动三
证明
(任选一组进行探究,并将本组证明过程写到白纸板上)
探究新知
已知: ABCD
求证:∠B=∠D,∠A=∠C.
A
B
C
D
证明:
补充:平行四边形邻角互补
起 点
第一站
第二站
第三站
终 点
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
探究新知
几何语言:
几何语言:
1、如图,在 □ABCD中,
若∠A+ ∠C= 220°,则∠A= 、 ∠B= 。
110°
70°
新知应用
2、如图,在 □ABCD中,
若□ABCD的周长为18cm,AB=4cm,则CB= .
5cm
新知应用
3、如图,在□ABCD中,点E、F在对角线 AC上,而且AE=CF,求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
在△ABE和△CDF中
∵
AB=CD
∠BAE=∠DCF
AE=CF
∴△ABE ≌△CDF(SAS)
∴BE=DF
新知应用
知识小结
一、知识点:
二、思想方法:
作业布置
必做题:习题6.1 第1、2题;
选做题:习题6.1 第3题;
实践作业:利用平行四边形设计精美的图案装饰数学学习角。
“智慧的追求永不停止”
我们下节课再见!
谢谢!
情景导入
6.1.1 平行四边形及其性质
青岛版 数学 八年级 下册
1、理解平行四边形的概念。
2、掌握平行四边形的性质,并灵活运用平行四边形的性质解决问题。
3、经历“猜想-验证-结论-证明”的过程,发展思维能力,培养探究意识。
用两个全等的三角形纸片拼出形状不同的四边形,其中哪些是平行四边形?为什么?
活动一
平行四边形的定义:
读作:
记作:
几何语言:
自主学习
在四边形ABCD中,
∵ AB // CD AD// BC
∴四边形ABCD是平行四边形
平行四边形ABCD
注:图形中字母的标识顺序应为顺时针方向或逆时针方向
两组对边分别平行的四边形叫做平行四边形
ABCD
对边: ;
对角: ;
对角线: 。
AB与CD,AD与BC
∠A与∠C,∠B与∠D
AC和BD
A
D
C
B
自主学习
不相邻的两个顶点连成的线段叫做对角线
探索之旅
第一站
猜想
1.平行四边形的对边具有哪些性质?
2.平行四边形的对角具有哪些性质?
能否验证你的猜想呢?
探究新知
第一站
第二站
验证
小组分工合作: 选择学具验证,并记录总结,代表汇报。
活动二
第一站
第二站
第三站
结论
1、平行四边形的两组对边分别相等。
2、平行四边形的两组对角分别相等。
探究新知
第一站
第二站
第三站
第四站
已知: ABCD
求证:①AB=CD,BC=DA;
②∠B=∠D,∠A=∠C.
A
B
C
D
活动三
证明
(任选一组进行探究,并将本组证明过程写到白纸板上)
探究新知
已知: ABCD
求证:∠B=∠D,∠A=∠C.
A
B
C
D
证明:
补充:平行四边形邻角互补
起 点
第一站
第二站
第三站
终 点
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
探究新知
几何语言:
几何语言:
1、如图,在 □ABCD中,
若∠A+ ∠C= 220°,则∠A= 、 ∠B= 。
110°
70°
新知应用
2、如图,在 □ABCD中,
若□ABCD的周长为18cm,AB=4cm,则CB= .
5cm
新知应用
3、如图,在□ABCD中,点E、F在对角线 AC上,而且AE=CF,求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
在△ABE和△CDF中
∵
AB=CD
∠BAE=∠DCF
AE=CF
∴△ABE ≌△CDF(SAS)
∴BE=DF
新知应用
知识小结
一、知识点:
二、思想方法:
作业布置
必做题:习题6.1 第1、2题;
选做题:习题6.1 第3题;
实践作业:利用平行四边形设计精美的图案装饰数学学习角。
“智慧的追求永不停止”
我们下节课再见!
谢谢!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
