人教版七年级上册6.3.2 角的比较与运算 第2课时 课件(共20张PPT)
文档属性
| 名称 | 人教版七年级上册6.3.2 角的比较与运算 第2课时 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 299.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
6.3.2 角的比较与运算
第2课时 角的平分线
学习目标
1.认识角的平分线及角的等分线,会画角的平分线.
学习重点
认识角的平分线
学习难点
角的平分线等有关的计算
角的比较与运算
比较
度量法
叠合法
线段的比较与运算
类比
数
形
角的和差
角的倍分
运算
A
B
O
C
思考:怎样找一个角的平分线?怎样表示?
探究新知
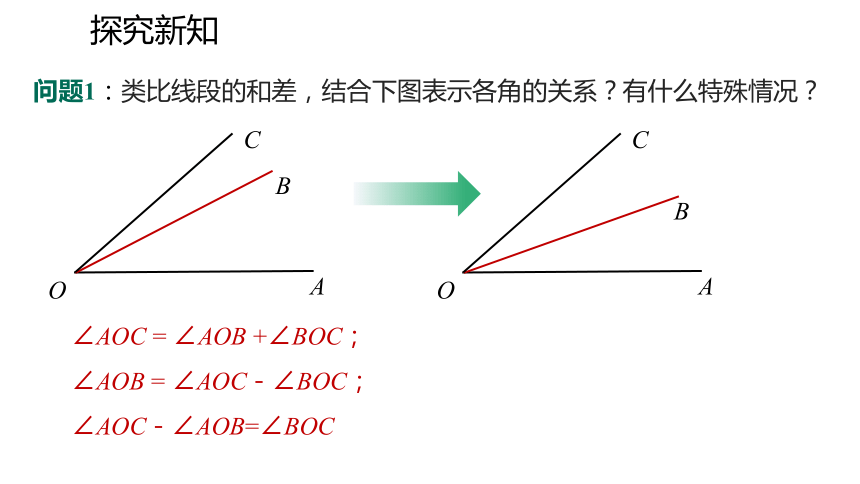
问题1:类比线段的和差,结合下图表示各角的关系?有什么特殊情况?
A
C
O
B
A
C
O
B
∠AOC = ∠AOB +∠BOC;
∠AOB = ∠AOC-∠BOC;
∠AOC-∠AOB=∠BOC
角的平分线
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC =∠AOB,
∠AOB =2∠BOC =2∠AOC.
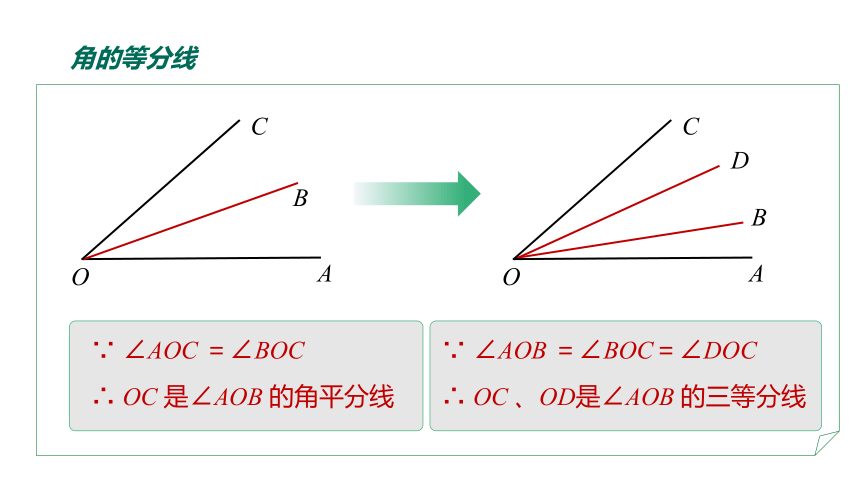
角的等分线
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
A
C
O
B
D
∵ ∠AOB =∠BOC=∠DOC
∴ OC 、OD是∠AOB 的三等分线
问题2:在作业本上画,怎样找出角平分线?
方法1:度量 方法2:对折
典例讲解
例1 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7
= 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
例2 如图,O 是直线 AB 上一点,∠AOC=53°17′,OB 是∠BOC 的平分线,求∠DOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
D
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
O
A
B
C
D
E
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,
∠AOC=80°,
所以∠BOC= ∠AOC
= ×80°=40°.
O
A
B
C
D
E
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
O
A
B
C
D
E
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以∠BOD =∠BOC+∠COD
= 40°+30°= 70°.
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
O
A
B
C
D
E
解:因为 ∠COD=30°,
OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
所以∠AOB= ∠AOC= ×80°= 40°.
2.如图②,若∠AOB= 60°,∠BOC=40°,则∠AOC= °.
1.如图①,若∠AOC=35°,∠BOC=40°,则 ∠AOB= °.
75
20
A
B
O
C
A
B
O
C
图① 图②
3.若∠AOB =60°,∠AOC =30°,则BOC= °.
90或30
课堂练习
4、一副三角板按如图方式摆放,已知∠1=5∠2,则∠1的度数是( )
A.15° B.18° C.72° D.75°
5、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是( )
A.20° B.40° C.50° D.80°
6. 如图,OC是平角∠AOB的角平分线,∠COD=32°, 求∠AOD的度数.
答案:∠AOD=122°.
O
A
B
C
D
7.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
O
A
D
C
B
解:设∠COD=x,
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x,
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.
8.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
(2) 若∠BOC=90°,求∠AOE的度数.
角的比较与运算
比较
度量法
叠合法
线段的比较与运算
类比
数
形
和差
倍分
运算
A
B
O
C
A
C
O
B
A
C
O
B
D
课堂小结
6.3.2 角的比较与运算
第2课时 角的平分线
学习目标
1.认识角的平分线及角的等分线,会画角的平分线.
学习重点
认识角的平分线
学习难点
角的平分线等有关的计算
角的比较与运算
比较
度量法
叠合法
线段的比较与运算
类比
数
形
角的和差
角的倍分
运算
A
B
O
C
思考:怎样找一个角的平分线?怎样表示?
探究新知
问题1:类比线段的和差,结合下图表示各角的关系?有什么特殊情况?
A
C
O
B
A
C
O
B
∠AOC = ∠AOB +∠BOC;
∠AOB = ∠AOC-∠BOC;
∠AOC-∠AOB=∠BOC
角的平分线
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC =∠AOB,
∠AOB =2∠BOC =2∠AOC.
角的等分线
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
A
C
O
B
D
∵ ∠AOB =∠BOC=∠DOC
∴ OC 、OD是∠AOB 的三等分线
问题2:在作业本上画,怎样找出角平分线?
方法1:度量 方法2:对折
典例讲解
例1 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7
= 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
例2 如图,O 是直线 AB 上一点,∠AOC=53°17′,OB 是∠BOC 的平分线,求∠DOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
D
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
O
A
B
C
D
E
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,
∠AOC=80°,
所以∠BOC= ∠AOC
= ×80°=40°.
O
A
B
C
D
E
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
O
A
B
C
D
E
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以∠BOD =∠BOC+∠COD
= 40°+30°= 70°.
例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
O
A
B
C
D
E
解:因为 ∠COD=30°,
OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
所以∠AOB= ∠AOC= ×80°= 40°.
2.如图②,若∠AOB= 60°,∠BOC=40°,则∠AOC= °.
1.如图①,若∠AOC=35°,∠BOC=40°,则 ∠AOB= °.
75
20
A
B
O
C
A
B
O
C
图① 图②
3.若∠AOB =60°,∠AOC =30°,则BOC= °.
90或30
课堂练习
4、一副三角板按如图方式摆放,已知∠1=5∠2,则∠1的度数是( )
A.15° B.18° C.72° D.75°
5、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是( )
A.20° B.40° C.50° D.80°
6. 如图,OC是平角∠AOB的角平分线,∠COD=32°, 求∠AOD的度数.
答案:∠AOD=122°.
O
A
B
C
D
7.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
O
A
D
C
B
解:设∠COD=x,
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x,
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.
8.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
(2) 若∠BOC=90°,求∠AOE的度数.
角的比较与运算
比较
度量法
叠合法
线段的比较与运算
类比
数
形
和差
倍分
运算
A
B
O
C
A
C
O
B
A
C
O
B
D
课堂小结
同课章节目录
