人教版 数学八年级上册 11.1.1 三角形的边 课件(共26张PPT)
文档属性
| 名称 | 人教版 数学八年级上册 11.1.1 三角形的边 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
第十一章 三角形
11.1 与三角形有关的线段
11.1.1 三角形的边
从这几幅图片中,你能发现哪些熟悉的几何图形呢?
1.理解三角形及其有关定义,认识三角形的边、角、顶点;
2.能用符号语言表示三角形,能把三角形按边的关系分类;
3.掌握三角形三边关系,并能用它解决相关问题。
A
B
C
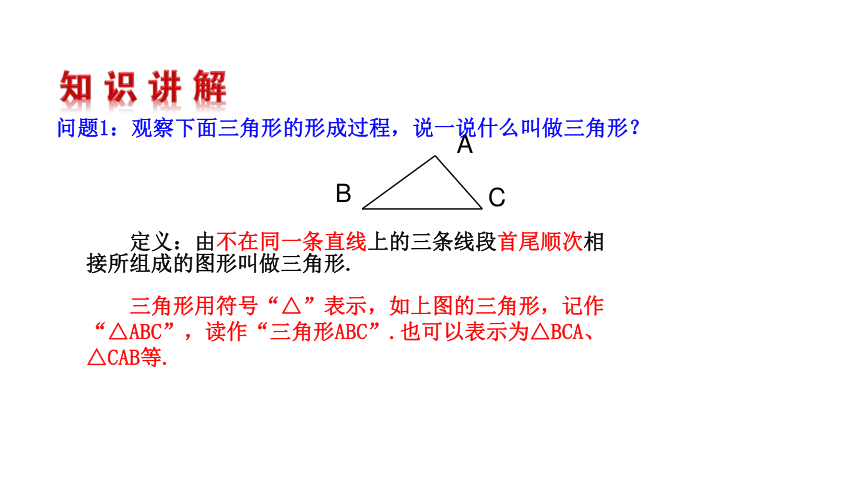
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题1:观察下面三角形的形成过程,说一说什么叫做三角形?
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.也可以表示为△BCA、△CAB等.
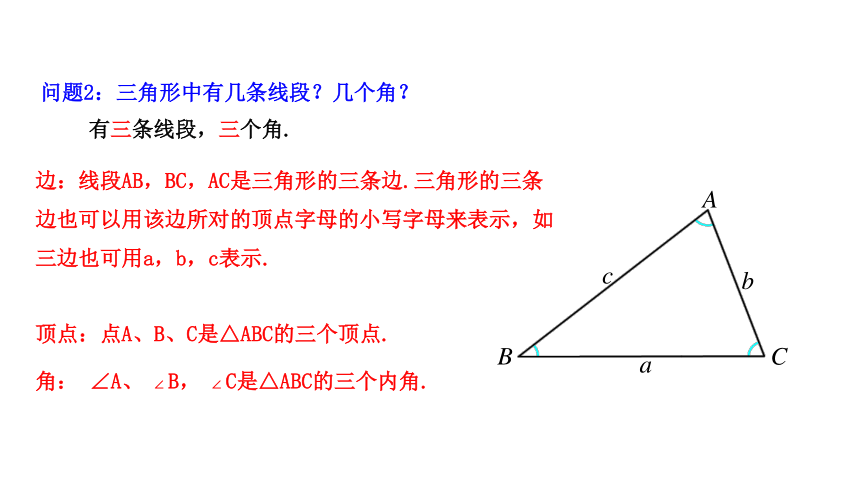
问题2:三角形中有几条线段?几个角?
有三条线段,三个角.
边:线段AB,BC,AC是三角形的三条边.三角形的三条边也可以用该边所对的顶点字母的小写字母来表示,如三边也可用a,b,c表示.
顶点:点A、B、C是△ABC的三个顶点.
角: ∠A、 ∠ B, ∠ C是△ABC的三个内角.
A
B
C
a
b
c
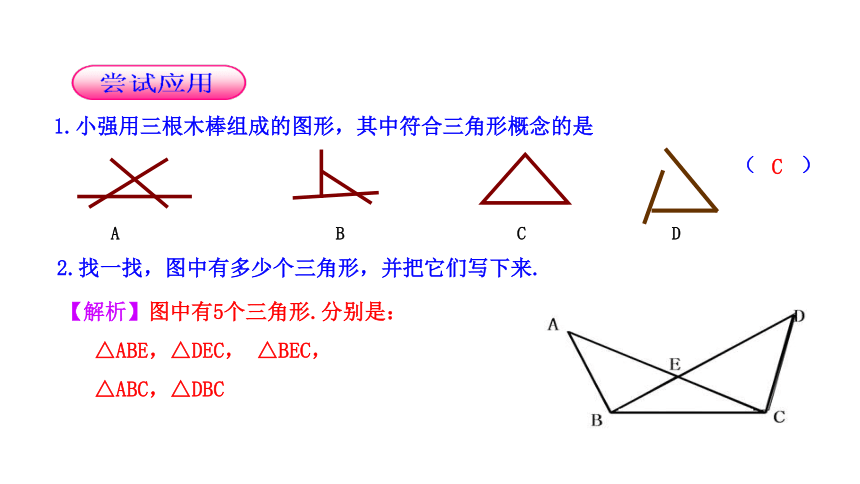
1.小强用三根木棒组成的图形,其中符合三角形概念的是
( )
B
A
C
C
2.找一找,图中有多少个三角形,并把它们写下来.
【解析】图中有5个三角形.分别是:
△ABE,△DEC, △BEC,
△ABC,△DBC
D
问题3:你能把三角形按边、角特征进行分类吗?
三角形按角分为:
直角三角形
锐角三角形
钝角三角形
三角形按边分为:
三边各不相等的三角形
腰与底边相等的等腰三角形
腰与底边不相等
的等腰三角形
等腰三角形
三角形
按角分类
锐角三角形
直角三角形
钝角三角形
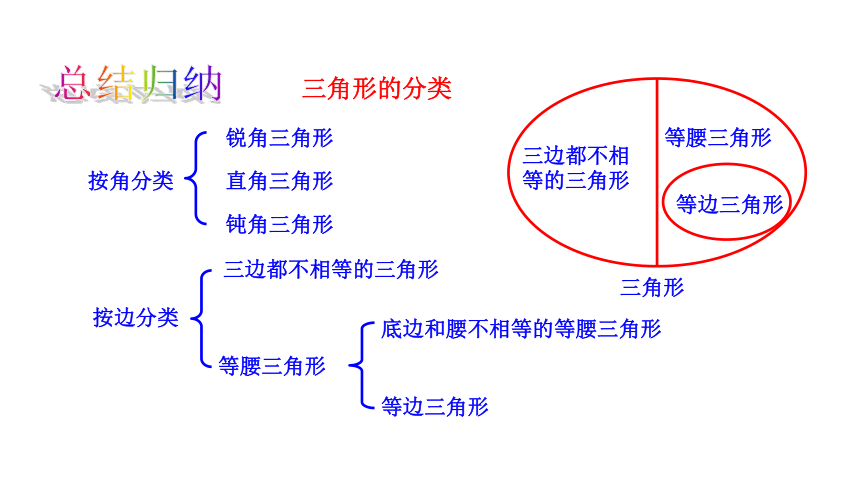
按边分类
三边都不相等的三角形
三角形的分类
等腰三角形
三边都不相等的三角形
等腰三角形
等边三角形
底边和腰不相等的等腰三角形
等边三角形
想一想:
三角形按边分类后等腰三角形包括等边三角形.等腰三角形相等的两边叫做腰,两腰的夹角叫做顶角,其余两角是底角.
按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
判断:
(1)一个钝角三角形一定不是等腰三角形.( )
(2)等边三角形是特殊的等腰三角形. ( )
(3)等腰三角形的腰和底一定不相等. ( )
(4)等边三角形是锐角三角形. ( )
(5)直角三角形一定不是等腰三角形. ( )
×
×
√
√
×
C
B
A
问题4:在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,难道小狗也懂数学?
因为:所有连接两点的线中,线段最短.即AC+BC>AB.
小结: 三角形两边的和大于第三边.即AC+BC>AB,把线段BC移项可得:AC>AB-BC,由此可得:三角形两边之差小于第三边.
他一步能走3米,你相信吗?
不可能
A
B
C
1.下列长度的三条线段能否组成三角形?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条线段的和都大于第三条线段?有没有更简便的判断方法?
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
50cm-30cm<第三根<50cm+30cm
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
2.某花店老板想做一个三角形支架,已经有了两根长为30厘米和50厘米的木棒,那么第三根木棒的长应该在什么范围内?
20cm<第三根<80cm
注意:在做题时,不仅要考虑到两边之和大于第三边,
还必须考虑到两边之差小于第三边.
若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
【解析】设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9.
根据两边之差小于第三边得:
x>7-2即x>5.
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7.
答:第三边的长为7.
例1
巩固并运用“三角形两边的和大于第三边”
用较小两条线段的和与第三条线段作比较;
若较小两条线段的和大于第三条线段,就能保证任意两条线段的和大于第三条线段.
追问 解决这类问题我们通常用哪两条线段的和与第三条线段做比较就可以了?为什么?
例2 用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?(2)能围成有一边的长是4cm的等腰三角形吗?为什么 ?
【解析】(1)设底边长为xcm,则腰长为2xcm,
x+2x+2x=18.
解得 x=3.6.
所以三边长分别为3.6cm、7.2cm、7.2cm.
(2)因为长为4cm的边可能是腰,也可能是底边,所以需要分情况讨论.
①若底边长为4cm,设腰长为xcm,则有
4+2x=18.
解得x=7.
②若腰长为4cm,设底边长为xcm,则有
2×4+x=18. 解得x=10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边长是4cm的等腰三角形.
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论.
(1)8 cm, 7 cm, 15 cm (2)13 cm, 12 cm, 20 cm
(3)5 cm, 5 cm, 11 cm
2.现有长度分别为1 cm,2 cm,3 cm,4 cm,5 cm的五条线段,
从其中选三条线段为边可以构成 个不同的三角形.
答案:(2)能摆成三角形
3
3.如果三角形的两边长分别是2和4,且第三边是奇数,
那么第三边长为 .若第三边为偶数,那么三角形的周
长为 .
3或5
10
【跟踪训练】
4.有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
解:取长度为2 cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13 cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
不重不漏
三边关系
原理
两点之间,线段最短
内容
两边之和大于第三边
两边之差小于第三边
a-bb,x为第三边)
应用
1.(徐州·中考)在如图所示的图形中,三角形的个数共有( )
A.1个 B.2个 C. 3个 D.4个
【解析】 图中有△ABC,△ABD,△ACD.
A
B
C
D
C
2.(徐州·中考)若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
【解析】设第三边长为xcm,根据三角形的三边关系可得:6-3<x<6+3,解得:3<x<9.
3.(绍兴·中考)长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4 B.5 C.6 D.7
【解析】①长度分别为5、3、4,能构成三角形,且最长边为5;②长度分别为2、6、4,不能构成三角形;③长度分别为2、7、3,不能构成三角形;④长度分别为6、3、3,不能构成三角形;综上所述,得到三角形的最长边长为5.
C
B
4.若△ABC的三边为a,b,c,则化简︱a+b-c︱+︱b-a-c︱的结果是( ).
A. 2a-2b B.2a+2b+2c C. 2a D. 2a-2c
【解析】根据三角形的三边关系得a+b-c>0,
b-a-c=b-(a+c)<0,所以原式=a+b-c-(b-a-c)
=a+b-c-b+a+c=2a.
C
5.已知,△ABC的三边长为4,9,x. (1)求△ABC的周长的取值范围; (2)当△ABC的周长为偶数时,求x.
【解析】(1)∵三角形的三边长分别为4,9,x, ∴9-4<x<9+4,即5<x<13, ∴9+4+5<△ABC的周长<9+4+13, 即:18<△ABC的周长<26; (2)∵△ABC的周长是偶数,由(1)结果得△ABC的周长可以是20,22或24,∴x的值为7,9或11.
天下兴亡,匹夫有责。
—— (清)顾炎武
第十一章 三角形
11.1 与三角形有关的线段
11.1.1 三角形的边
从这几幅图片中,你能发现哪些熟悉的几何图形呢?
1.理解三角形及其有关定义,认识三角形的边、角、顶点;
2.能用符号语言表示三角形,能把三角形按边的关系分类;
3.掌握三角形三边关系,并能用它解决相关问题。
A
B
C
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题1:观察下面三角形的形成过程,说一说什么叫做三角形?
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.也可以表示为△BCA、△CAB等.
问题2:三角形中有几条线段?几个角?
有三条线段,三个角.
边:线段AB,BC,AC是三角形的三条边.三角形的三条边也可以用该边所对的顶点字母的小写字母来表示,如三边也可用a,b,c表示.
顶点:点A、B、C是△ABC的三个顶点.
角: ∠A、 ∠ B, ∠ C是△ABC的三个内角.
A
B
C
a
b
c
1.小强用三根木棒组成的图形,其中符合三角形概念的是
( )
B
A
C
C
2.找一找,图中有多少个三角形,并把它们写下来.
【解析】图中有5个三角形.分别是:
△ABE,△DEC, △BEC,
△ABC,△DBC
D
问题3:你能把三角形按边、角特征进行分类吗?
三角形按角分为:
直角三角形
锐角三角形
钝角三角形
三角形按边分为:
三边各不相等的三角形
腰与底边相等的等腰三角形
腰与底边不相等
的等腰三角形
等腰三角形
三角形
按角分类
锐角三角形
直角三角形
钝角三角形
按边分类
三边都不相等的三角形
三角形的分类
等腰三角形
三边都不相等的三角形
等腰三角形
等边三角形
底边和腰不相等的等腰三角形
等边三角形
想一想:
三角形按边分类后等腰三角形包括等边三角形.等腰三角形相等的两边叫做腰,两腰的夹角叫做顶角,其余两角是底角.
按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
判断:
(1)一个钝角三角形一定不是等腰三角形.( )
(2)等边三角形是特殊的等腰三角形. ( )
(3)等腰三角形的腰和底一定不相等. ( )
(4)等边三角形是锐角三角形. ( )
(5)直角三角形一定不是等腰三角形. ( )
×
×
√
√
×
C
B
A
问题4:在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,难道小狗也懂数学?
因为:所有连接两点的线中,线段最短.即AC+BC>AB.
小结: 三角形两边的和大于第三边.即AC+BC>AB,把线段BC移项可得:AC>AB-BC,由此可得:三角形两边之差小于第三边.
他一步能走3米,你相信吗?
不可能
A
B
C
1.下列长度的三条线段能否组成三角形?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条线段的和都大于第三条线段?有没有更简便的判断方法?
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
50cm-30cm<第三根<50cm+30cm
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
2.某花店老板想做一个三角形支架,已经有了两根长为30厘米和50厘米的木棒,那么第三根木棒的长应该在什么范围内?
20cm<第三根<80cm
注意:在做题时,不仅要考虑到两边之和大于第三边,
还必须考虑到两边之差小于第三边.
若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
【解析】设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9.
根据两边之差小于第三边得:
x>7-2即x>5.
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7.
答:第三边的长为7.
例1
巩固并运用“三角形两边的和大于第三边”
用较小两条线段的和与第三条线段作比较;
若较小两条线段的和大于第三条线段,就能保证任意两条线段的和大于第三条线段.
追问 解决这类问题我们通常用哪两条线段的和与第三条线段做比较就可以了?为什么?
例2 用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?(2)能围成有一边的长是4cm的等腰三角形吗?为什么 ?
【解析】(1)设底边长为xcm,则腰长为2xcm,
x+2x+2x=18.
解得 x=3.6.
所以三边长分别为3.6cm、7.2cm、7.2cm.
(2)因为长为4cm的边可能是腰,也可能是底边,所以需要分情况讨论.
①若底边长为4cm,设腰长为xcm,则有
4+2x=18.
解得x=7.
②若腰长为4cm,设底边长为xcm,则有
2×4+x=18. 解得x=10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边长是4cm的等腰三角形.
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论.
(1)8 cm, 7 cm, 15 cm (2)13 cm, 12 cm, 20 cm
(3)5 cm, 5 cm, 11 cm
2.现有长度分别为1 cm,2 cm,3 cm,4 cm,5 cm的五条线段,
从其中选三条线段为边可以构成 个不同的三角形.
答案:(2)能摆成三角形
3
3.如果三角形的两边长分别是2和4,且第三边是奇数,
那么第三边长为 .若第三边为偶数,那么三角形的周
长为 .
3或5
10
【跟踪训练】
4.有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
解:取长度为2 cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13 cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
不重不漏
三边关系
原理
两点之间,线段最短
内容
两边之和大于第三边
两边之差小于第三边
a-b
应用
1.(徐州·中考)在如图所示的图形中,三角形的个数共有( )
A.1个 B.2个 C. 3个 D.4个
【解析】 图中有△ABC,△ABD,△ACD.
A
B
C
D
C
2.(徐州·中考)若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
【解析】设第三边长为xcm,根据三角形的三边关系可得:6-3<x<6+3,解得:3<x<9.
3.(绍兴·中考)长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4 B.5 C.6 D.7
【解析】①长度分别为5、3、4,能构成三角形,且最长边为5;②长度分别为2、6、4,不能构成三角形;③长度分别为2、7、3,不能构成三角形;④长度分别为6、3、3,不能构成三角形;综上所述,得到三角形的最长边长为5.
C
B
4.若△ABC的三边为a,b,c,则化简︱a+b-c︱+︱b-a-c︱的结果是( ).
A. 2a-2b B.2a+2b+2c C. 2a D. 2a-2c
【解析】根据三角形的三边关系得a+b-c>0,
b-a-c=b-(a+c)<0,所以原式=a+b-c-(b-a-c)
=a+b-c-b+a+c=2a.
C
5.已知,△ABC的三边长为4,9,x. (1)求△ABC的周长的取值范围; (2)当△ABC的周长为偶数时,求x.
【解析】(1)∵三角形的三边长分别为4,9,x, ∴9-4<x<9+4,即5<x<13, ∴9+4+5<△ABC的周长<9+4+13, 即:18<△ABC的周长<26; (2)∵△ABC的周长是偶数,由(1)结果得△ABC的周长可以是20,22或24,∴x的值为7,9或11.
天下兴亡,匹夫有责。
—— (清)顾炎武
