人教版 数学八年级上册 11.2.2 三角形的外角 课件(共23张PPT)
文档属性
| 名称 | 人教版 数学八年级上册 11.2.2 三角形的外角 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 781.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 13:58:41 | ||
图片预览








文档简介
(共23张PPT)
11.2.2 三角形的外角
A
B
C
D
E
同学们,你们知不知道国旗上的五角星的五个角的和是多少度
A
B
C
D
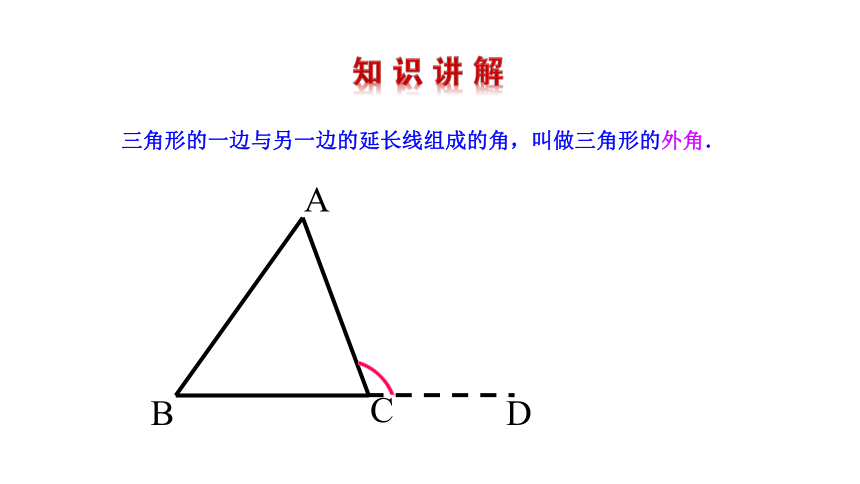
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
问题1 如图∠ACD是△ABC的一个外角,那么延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠DCE不是△ABC的一个外角
问题2 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
∠ACD是△ABC的一个外角
∠BCE是△ABC的一个外角
画一个△ABC ,你能画出它的所有外角吗?请动手试一试.
同时想一想△ABC的外角共有几个呢?
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,它们相等.
注:每个外角与相应的内角互为补角.
A
B
C
D
E
若∠BAC=55°,∠ B=60°,试求∠ ACB, ∠ACD, ∠CAE的度数.
分别是65°,115°,125°
图中哪些角是三角形的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
通过上题的计算,你发现∠ACD, ∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.你能简述一下推导过程吗?
∠ACD= ∠BAC+∠B; ∠ACD+ ∠ACB=180°.
∠CAE= ∠ACB+∠B; ∠CAE+ ∠BAC=180°.
A
B
C
D
E
2.三角形的一个外角等于与它不相邻的两个内角的和.
1.三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系
三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
练一练:说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80 °
60 °
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50 °
32 °
(2)
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
∴∠DAB=∠1 + ∠3
∴ ∠DAB+∠EBC+∠FCA= 2(∠1 + ∠2 +∠3)
又∵ ∠1 + ∠2 +∠3 = 180°
∴ ∠DAB+∠EBC+∠FCA=360°
∵∠DAB、∠EBC 、∠FCA是 △ABC的外角
例 如图∠DAB、∠EBC 、∠FCA是△ABC的外角,求它们的和是多少?
∠EBC=∠2 + ∠3
∠FCA=∠1 + ∠2
(三角形内角和定理)
(三角形的外角等于和与它不相邻的两个内角的和)
三角形的外角和等于360°
例题
判断题:
1、三角形的外角和等于它内角和的2倍. ( )
2、三角形的一个外角等于两个内角的和.( )
3、三角形的一个外角大于任何一个内角.( )
4、三角形的一个内角小于任何一个与它不相邻的外角.( )
A
B
C
D
已知图中∠A、∠B、∠C分别为80°,20°,30° ,求∠1的度数
B
2
1
A
C
D
E
解:∵∠1=∠2+∠B,
∠2=∠A+∠C,
∴∠1=∠A+∠B+∠C
=80°+20°+30°
=130°
如图,试计算∠BOC的度数.
80
30
20
A
B
C
O
D
⌒
100°
解:延长BO交AC于点D,则
∠ODC=∠A+∠B=80°+20°=100°,
∠BOC=∠ODC+∠C=100°+30°=130°
已知:五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角
∴ ∠1=∠B+∠D
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
又∵∠A+∠1+∠2=180°( )
又 ∵ ∠2是△EHC的一个外角
∴ ∠2=∠C+∠E
A
B
C
D
E
∴ ∠A+∠B+∠C+∠D+∠E =180°
F
1
H
2
1
2
三角形的外角
定义
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
1.已知△ABC的一个外角为50°,则△ABC一定是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角三角形或锐角三角形
【解析】△ABC的一个外角为50°,则与这个外角相邻的内角是130°,所以△ABC一定是钝角三角形.
B
2. (2020 吉林中考)将一副三角尺按如图所示的方式摆放,则
∠α的大小为( )
A.85° B.75° C.65° D.60°
∠α=∠E+∠ACB=30°+45°=75°.
解析: 如图所示,
B
3.(2020 锦州中考)如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
A.80° B.90° C.100° D.110°
解析:∵∠A=30°,∠B=50°,
∴∠ACB=180°-30°-50°=100°(三角形内角和定义).
∵CD平分∠ACB,
∴∠BCD=
∠ACB=
×100°=50°,
C
∴∠ADC=∠BCD+∠B=50°+50°=100°.
解析:∵∠B=90°,∠A=45°,∴∠ACB=45°. ∵∠EDF=90°,∠F=60°,∴∠DEF=30°. ∵EF∥BC,∴∠EDC=∠DEF=30°, ∴∠CED=∠ACB-∠EDC=45°-30°=15°.
4.(2020 湖北中考)将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是( )
A.15° B.20°
C.25° D.30°
A
∠A+∠B+∠C+∠D+∠E+∠F= .
360°
A
D
E
C
F
B
1
2
3
P
3
5.
第一个青春是上帝给的;第二个青春是靠自己努力得到的.
11.2.2 三角形的外角
A
B
C
D
E
同学们,你们知不知道国旗上的五角星的五个角的和是多少度
A
B
C
D
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
问题1 如图∠ACD是△ABC的一个外角,那么延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠DCE不是△ABC的一个外角
问题2 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
∠ACD是△ABC的一个外角
∠BCE是△ABC的一个外角
画一个△ABC ,你能画出它的所有外角吗?请动手试一试.
同时想一想△ABC的外角共有几个呢?
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,它们相等.
注:每个外角与相应的内角互为补角.
A
B
C
D
E
若∠BAC=55°,∠ B=60°,试求∠ ACB, ∠ACD, ∠CAE的度数.
分别是65°,115°,125°
图中哪些角是三角形的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
通过上题的计算,你发现∠ACD, ∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.你能简述一下推导过程吗?
∠ACD= ∠BAC+∠B; ∠ACD+ ∠ACB=180°.
∠CAE= ∠ACB+∠B; ∠CAE+ ∠BAC=180°.
A
B
C
D
E
2.三角形的一个外角等于与它不相邻的两个内角的和.
1.三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系
三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
练一练:说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80 °
60 °
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50 °
32 °
(2)
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
∴∠DAB=∠1 + ∠3
∴ ∠DAB+∠EBC+∠FCA= 2(∠1 + ∠2 +∠3)
又∵ ∠1 + ∠2 +∠3 = 180°
∴ ∠DAB+∠EBC+∠FCA=360°
∵∠DAB、∠EBC 、∠FCA是 △ABC的外角
例 如图∠DAB、∠EBC 、∠FCA是△ABC的外角,求它们的和是多少?
∠EBC=∠2 + ∠3
∠FCA=∠1 + ∠2
(三角形内角和定理)
(三角形的外角等于和与它不相邻的两个内角的和)
三角形的外角和等于360°
例题
判断题:
1、三角形的外角和等于它内角和的2倍. ( )
2、三角形的一个外角等于两个内角的和.( )
3、三角形的一个外角大于任何一个内角.( )
4、三角形的一个内角小于任何一个与它不相邻的外角.( )
A
B
C
D
已知图中∠A、∠B、∠C分别为80°,20°,30° ,求∠1的度数
B
2
1
A
C
D
E
解:∵∠1=∠2+∠B,
∠2=∠A+∠C,
∴∠1=∠A+∠B+∠C
=80°+20°+30°
=130°
如图,试计算∠BOC的度数.
80
30
20
A
B
C
O
D
⌒
100°
解:延长BO交AC于点D,则
∠ODC=∠A+∠B=80°+20°=100°,
∠BOC=∠ODC+∠C=100°+30°=130°
已知:五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角
∴ ∠1=∠B+∠D
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
又∵∠A+∠1+∠2=180°( )
又 ∵ ∠2是△EHC的一个外角
∴ ∠2=∠C+∠E
A
B
C
D
E
∴ ∠A+∠B+∠C+∠D+∠E =180°
F
1
H
2
1
2
三角形的外角
定义
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
1.已知△ABC的一个外角为50°,则△ABC一定是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角三角形或锐角三角形
【解析】△ABC的一个外角为50°,则与这个外角相邻的内角是130°,所以△ABC一定是钝角三角形.
B
2. (2020 吉林中考)将一副三角尺按如图所示的方式摆放,则
∠α的大小为( )
A.85° B.75° C.65° D.60°
∠α=∠E+∠ACB=30°+45°=75°.
解析: 如图所示,
B
3.(2020 锦州中考)如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
A.80° B.90° C.100° D.110°
解析:∵∠A=30°,∠B=50°,
∴∠ACB=180°-30°-50°=100°(三角形内角和定义).
∵CD平分∠ACB,
∴∠BCD=
∠ACB=
×100°=50°,
C
∴∠ADC=∠BCD+∠B=50°+50°=100°.
解析:∵∠B=90°,∠A=45°,∴∠ACB=45°. ∵∠EDF=90°,∠F=60°,∴∠DEF=30°. ∵EF∥BC,∴∠EDC=∠DEF=30°, ∴∠CED=∠ACB-∠EDC=45°-30°=15°.
4.(2020 湖北中考)将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是( )
A.15° B.20°
C.25° D.30°
A
∠A+∠B+∠C+∠D+∠E+∠F= .
360°
A
D
E
C
F
B
1
2
3
P
3
5.
第一个青春是上帝给的;第二个青春是靠自己努力得到的.
