人教版 数学八年级上册 11.3 多边形及其内角和 课件(共31张PPT)
文档属性
| 名称 | 人教版 数学八年级上册 11.3 多边形及其内角和 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 14:00:17 | ||
图片预览



文档简介
(共31张PPT)
11.3 多边形及其内角和
*
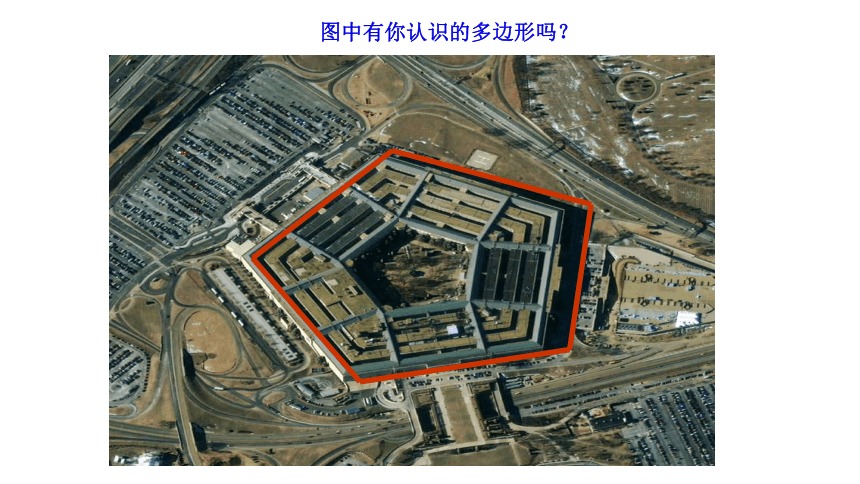
图中有你认识的多边形吗?
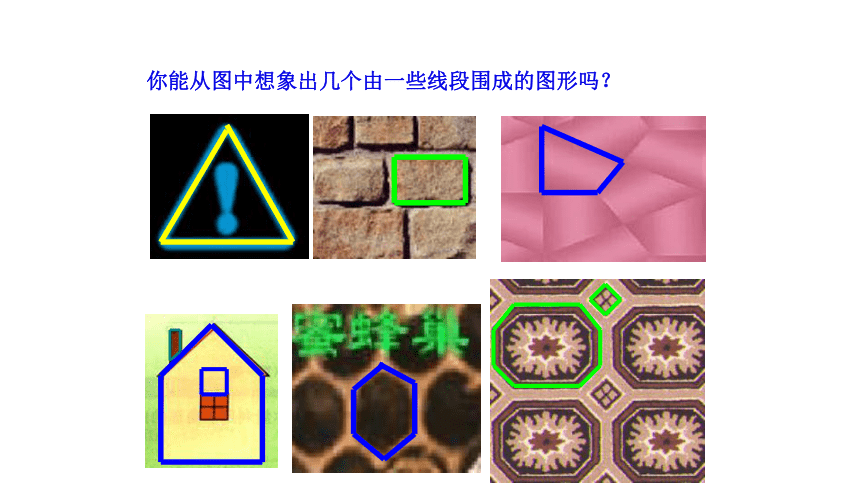
你能从图中想象出几个由一些线段围成的图形吗?
1.了解多边形及有关概念,理解正多边形及其有关概念;
2.区别凸多边形与凹多边形;
3.了解多边形内角和与外角和的探究过程;
4.掌握多边形内角和与外角和定理;
5. 感受数学知识在实际生活中的应用.
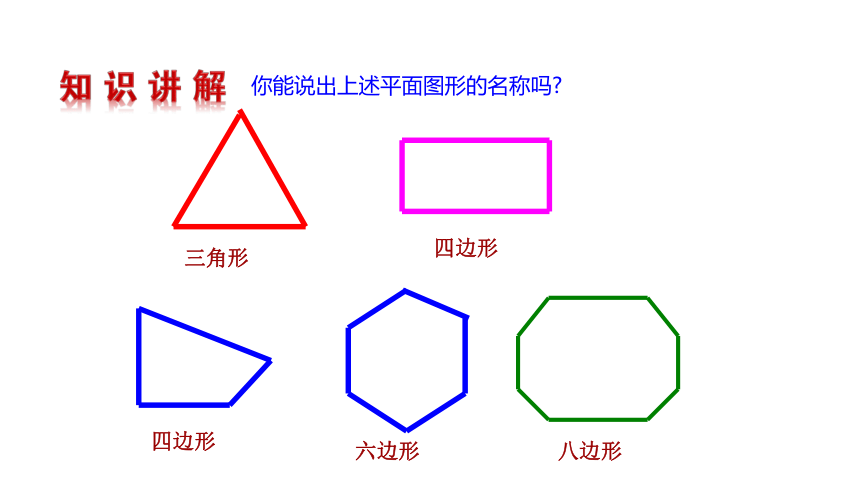
你能说出上述平面图形的名称吗
三角形
四边形
四边形
六边形
八边形
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
你能仿照三角形的定义给出四边形、五边形……的定义吗?
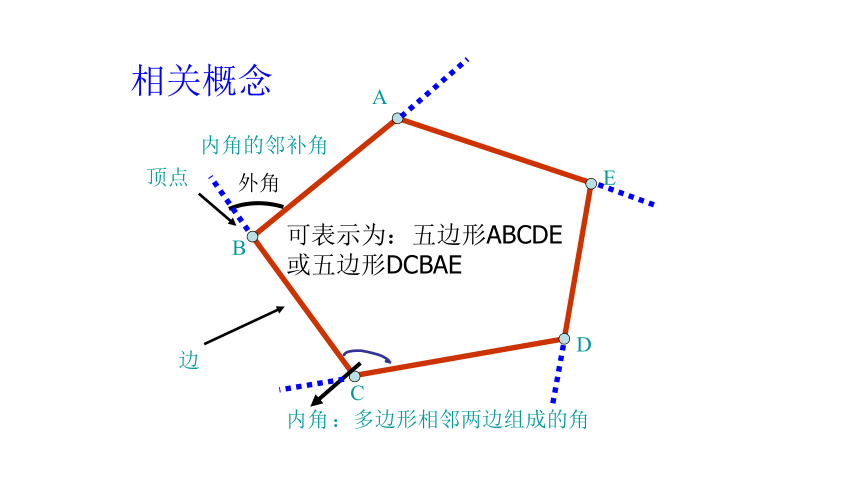
相关概念
顶点
内角
边
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
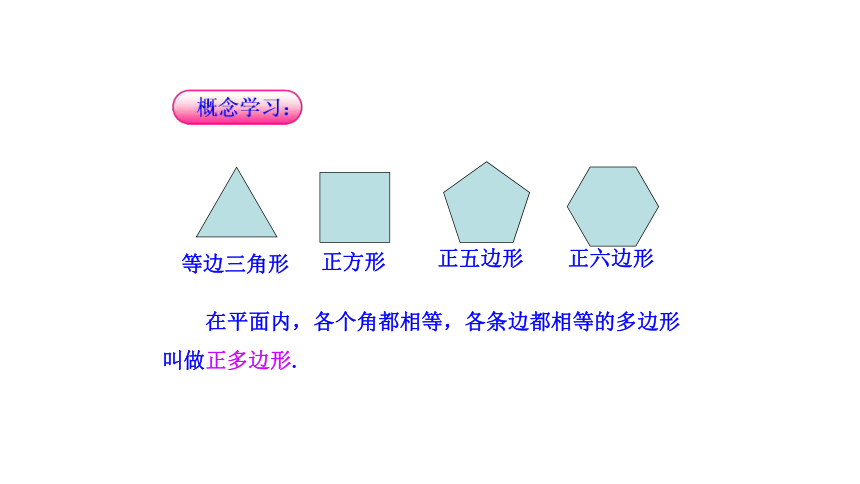
在平面内,各个角都相等,各条边都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
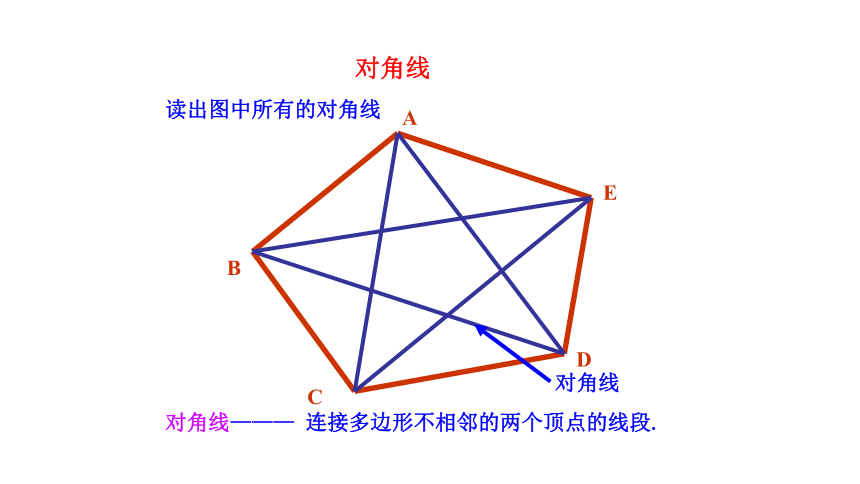
对角线
对角线
对角线——— 连接多边形不相邻的两个顶点的线段.
A
B
C
D
E
读出图中所有的对角线
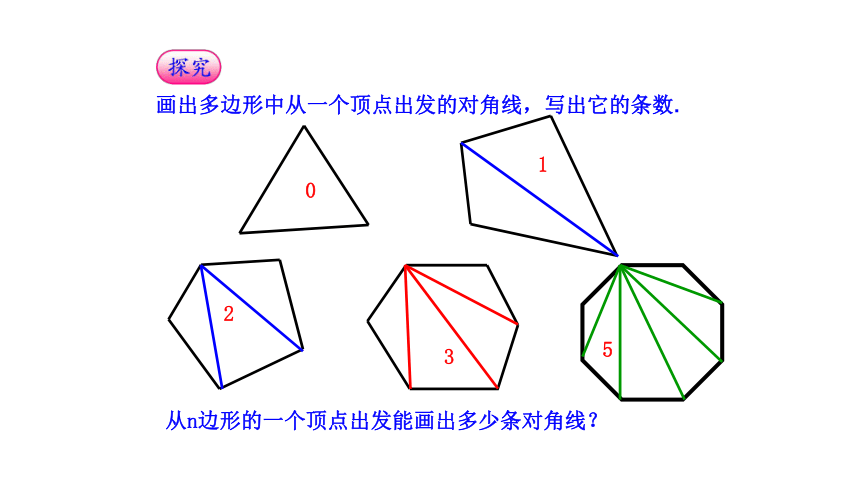
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
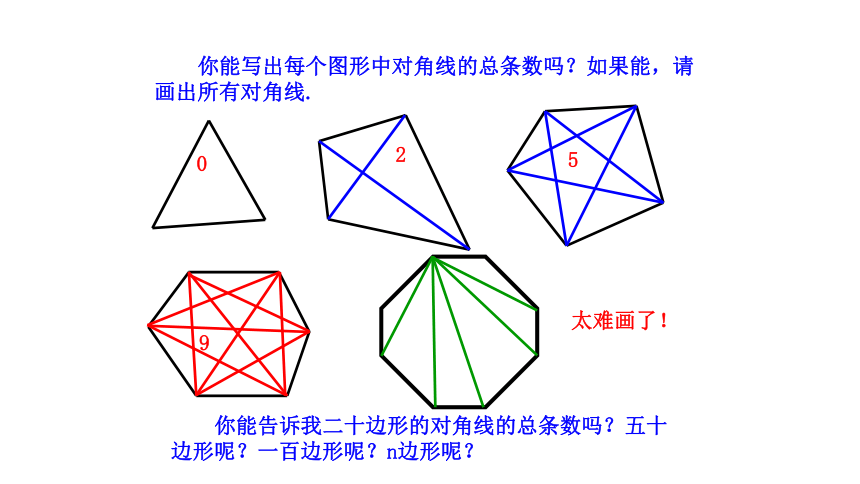
你能写出每个图形中对角线的总条数吗?如果能,请画出所有对角线.
0
2
5
9
你能告诉我二十边形的对角线的总条数吗?五十边形呢?一百边形呢?n边形呢?
太难画了!
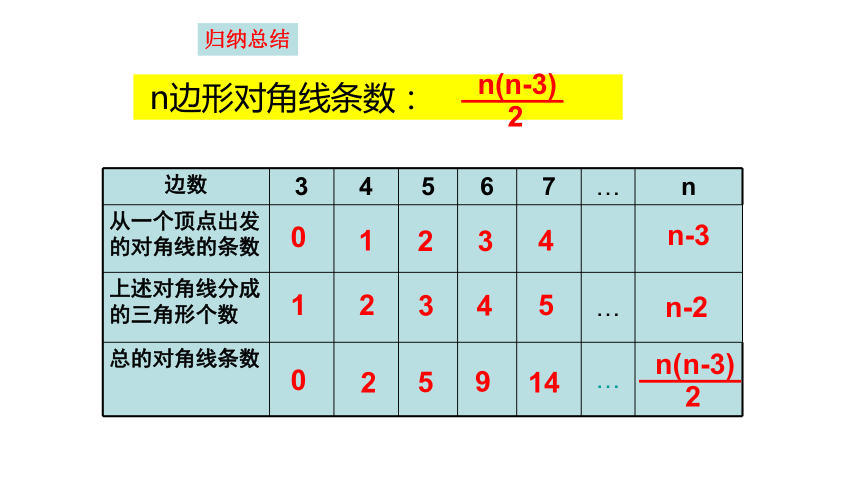
归纳总结
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
n边形对角线条数:
n(n-3)
2
观察 你能说出这两幅图形的异同点吗?
(1)
(2)
凸四边形
凹四边形
*
A
B
C
D
A
B
C
D
图1
图2
如图2,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
如图1,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
5、多边形分为___________和____________两类.
4、正多边形的_____相等,____相等.
3、从五边形的一个顶点出发可以画_____条对角线,它们将五边形分成______个三角形.
2、四边形有_____条对角线。五边形有______条对角线。四边形的一条对角线将它分成______个三角形.
1、n边形有______个顶点,_____条边,有_____个角,有________个不共顶点外角.
n
n
n
n
2
5
2
3
2
边
角
凸多边形
凹多边形
跟踪训练
问题2 你知道长方形和正方形的内角和是多少 度?
问题1 三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
问题3 猜想任意四边形的内角和是多少度?
多边形的内角和
猜想:四边形ABCD的内角和是360°.
问题4 你能用以前学过的知识说明一下你的结论吗?
猜想与证明
方法:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
B
A
C
D
E
五边形的内角和是多少呢?你能类比上面的方法求出结果吗?
五边形内角和=3×180°=540°
多边形 边数 一个顶点出发的对角线条数 图形
分成三角形的个数 内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
因为
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
典例精析
多边形的外角和
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
与边数无关
问题:回想正n边形的性质,你知道正n边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:
1.(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是
______边形.
六
八
2.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360 ,
∴ (n-2) 180°=2× 360 。
解得: n=6
∴这个多边形的边数为6.
课堂小结
2.如果多边形有n条边,从多边形的一个顶点出发可以画出n-3条对角线,一共有 条对角线.
1.多边形
凹多边形
凸多边形
正多边形
角相等 边相等
本节主要内容:
3.多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
(1)十二边形的内角和是( ).
(2)一个多边形当边数增加1时,它的内角和增加( ).
(3)一个多边形的内角和是720 ,则此多边形共有( )个内角.
(4) 如果一个多边形的内角和是1440 ,那么它是( )边形.
1800
180
六
十
2.一个多边形的内角和是外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
C
3.求下列图形中的x的值。
60°
95°
4.在四边形ABCD中,∠A=120°,∠B:∠C:∠D
=3:4:5,求∠B,∠C,∠D的度数.
【解析】设∠B,∠C,∠D的度数分别是3x°,4x°,5x°,由四边形的内角和等于360°可得:
120 + 3x + 4x + 5x = 360,
12x = 240,
x=20,
∴ 3x = 60,
4x = 80,
5x = 100.
答:∠B,∠C,∠D的度数分别为60°,80°,100°.
绳锯木断,水滴石穿。
—— 罗大经
11.3 多边形及其内角和
*
图中有你认识的多边形吗?
你能从图中想象出几个由一些线段围成的图形吗?
1.了解多边形及有关概念,理解正多边形及其有关概念;
2.区别凸多边形与凹多边形;
3.了解多边形内角和与外角和的探究过程;
4.掌握多边形内角和与外角和定理;
5. 感受数学知识在实际生活中的应用.
你能说出上述平面图形的名称吗
三角形
四边形
四边形
六边形
八边形
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
你能仿照三角形的定义给出四边形、五边形……的定义吗?
相关概念
顶点
内角
边
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
在平面内,各个角都相等,各条边都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
对角线
对角线
对角线——— 连接多边形不相邻的两个顶点的线段.
A
B
C
D
E
读出图中所有的对角线
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
你能写出每个图形中对角线的总条数吗?如果能,请画出所有对角线.
0
2
5
9
你能告诉我二十边形的对角线的总条数吗?五十边形呢?一百边形呢?n边形呢?
太难画了!
归纳总结
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
n边形对角线条数:
n(n-3)
2
观察 你能说出这两幅图形的异同点吗?
(1)
(2)
凸四边形
凹四边形
*
A
B
C
D
A
B
C
D
图1
图2
如图2,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
如图1,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
5、多边形分为___________和____________两类.
4、正多边形的_____相等,____相等.
3、从五边形的一个顶点出发可以画_____条对角线,它们将五边形分成______个三角形.
2、四边形有_____条对角线。五边形有______条对角线。四边形的一条对角线将它分成______个三角形.
1、n边形有______个顶点,_____条边,有_____个角,有________个不共顶点外角.
n
n
n
n
2
5
2
3
2
边
角
凸多边形
凹多边形
跟踪训练
问题2 你知道长方形和正方形的内角和是多少 度?
问题1 三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
问题3 猜想任意四边形的内角和是多少度?
多边形的内角和
猜想:四边形ABCD的内角和是360°.
问题4 你能用以前学过的知识说明一下你的结论吗?
猜想与证明
方法:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
B
A
C
D
E
五边形的内角和是多少呢?你能类比上面的方法求出结果吗?
五边形内角和=3×180°=540°
多边形 边数 一个顶点出发的对角线条数 图形
分成三角形的个数 内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
因为
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
典例精析
多边形的外角和
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
与边数无关
问题:回想正n边形的性质,你知道正n边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:
1.(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是
______边形.
六
八
2.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360 ,
∴ (n-2) 180°=2× 360 。
解得: n=6
∴这个多边形的边数为6.
课堂小结
2.如果多边形有n条边,从多边形的一个顶点出发可以画出n-3条对角线,一共有 条对角线.
1.多边形
凹多边形
凸多边形
正多边形
角相等 边相等
本节主要内容:
3.多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
(1)十二边形的内角和是( ).
(2)一个多边形当边数增加1时,它的内角和增加( ).
(3)一个多边形的内角和是720 ,则此多边形共有( )个内角.
(4) 如果一个多边形的内角和是1440 ,那么它是( )边形.
1800
180
六
十
2.一个多边形的内角和是外角和的2倍,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
C
3.求下列图形中的x的值。
60°
95°
4.在四边形ABCD中,∠A=120°,∠B:∠C:∠D
=3:4:5,求∠B,∠C,∠D的度数.
【解析】设∠B,∠C,∠D的度数分别是3x°,4x°,5x°,由四边形的内角和等于360°可得:
120 + 3x + 4x + 5x = 360,
12x = 240,
x=20,
∴ 3x = 60,
4x = 80,
5x = 100.
答:∠B,∠C,∠D的度数分别为60°,80°,100°.
绳锯木断,水滴石穿。
—— 罗大经
