人教版 数学八年级上册 11.1.3三角形的稳定性 课件(共30张PPT)
文档属性
| 名称 | 人教版 数学八年级上册 11.1.3三角形的稳定性 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 14:03:10 | ||
图片预览








文档简介
(共30张PPT)
11.1.2 三角形的高、中线与角平分线
11.1.3 三角形的稳定性
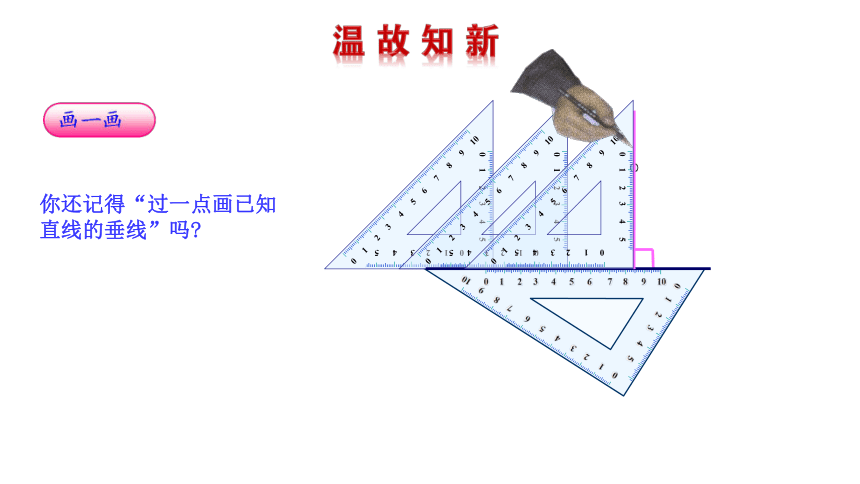
你还记得“过一点画已知
直线的垂线”吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
1.理解三角形的高,中线,角平分线等概念.
2.会画三角形的高,中线,角平分线.(重点)
3.了解三角形的稳定性.
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高线,
简称三角形的高。
如图所示, 线段AD是BC边上的高.
任意画一个锐角△ABC,
A
B
C
请你画出BC边上的高.
注意:
标明 垂直的记号和垂足的字母
D
1.三角形的高:
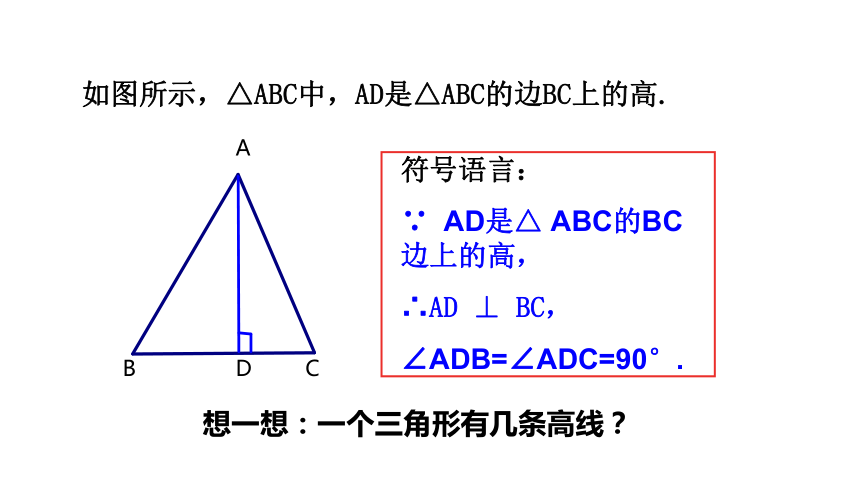
如图所示,△ABC中,AD是△ABC的边BC上的高.
符号语言:
∵ AD是△ ABC的BC边上的高,
∴AD ⊥ BC,
∠ADB=∠ADC=90°.
A
B
C
D
想一想:一个三角形有几条高线?
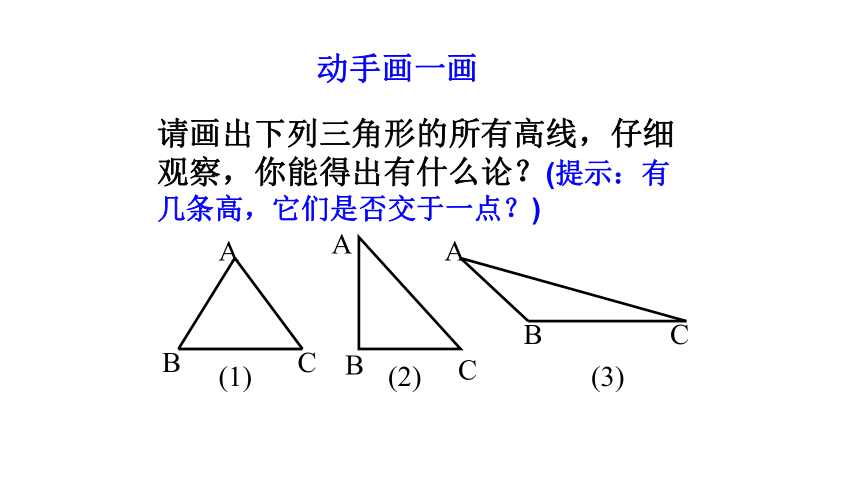
动手画一画
请画出下列三角形的所有高线,仔细观察,你能得出有什么论?(提示:有几条高,它们是否交于一点?)
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
O
A
B
D
E
F
A
B
C
(D)
●
A
B
C
D
F
E
O
(O)
●
●
C
E
(F)
归纳:1 、锐角三角形的三条高交于内部一点
2、直角三角形的三条高交于直角顶点
3、钝角三角形的三条高所在直线交于外部一点
4、三角形三条高线的交点叫做三角形的垂心.
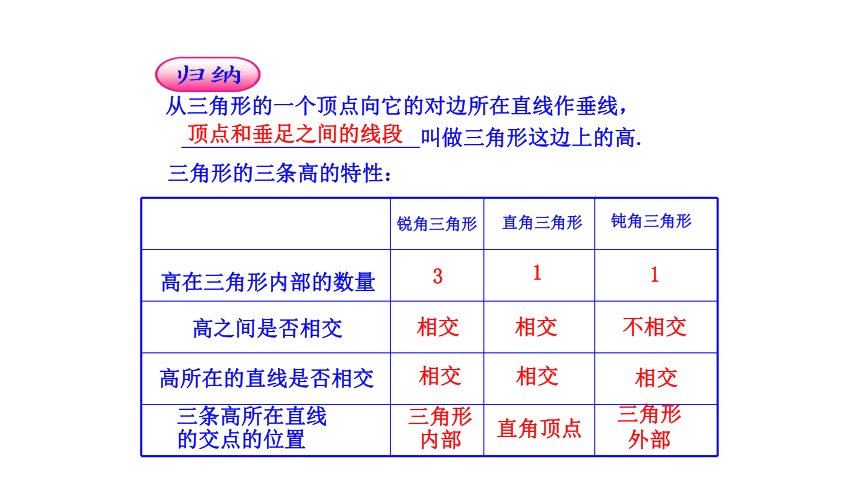
从三角形的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边上的高.
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
1.下列各组图形中,哪一组图形中的AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
在三角形中,连接一个顶点与它对边中点
的线段,叫做这个三角形的中线.
A
B
C
D
符号语言:
∵AD是△ ABC的 中线
∴BD =CD = BC
1
2
※ 拓展:三角形的中线把它分成面积相等的两个三角形
2.三角形的中线:
请画出下列三角形的所有中线,仔细观察,你能得出有什么论?
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
G
G
G
●
●
●
归纳:
1 、任意三角形的三条中线都在三角形的内部,并且交于一点.
2、三角形三条中线的交点叫做三角形的重心.
A
B
C
D
符号语言:
∵AD是 △ ABC的
角平分线
∴∠ BAD = ∠ CAD
=
1
2
∠BAC
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
思考:三角形的角平分线和角的平分线有什么区别?
3.三角形的角平分线:
三角形的角平分线是一条线段,角的平分线是一条射线.
探究交流
请画出下列三角形的所有角平分线,仔细观察,你能得出有什么论?
归纳:
1 、任意三角形的三条角平分线都在三角形的内部,并且交于一点.
2、三角形三条角平分线的交点叫做三角形的内心.
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
I
I
I
●
●
●
2
2
BD
6 cm
练习1.如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .
A
B
C
D
E
F
G
2.如图,AD,BE,CF 是△ABC 的三条角平分线,则:
∠1 = ;
∠3 = ;
∠ACB = 2 .
∠2
∠ABC
∠4
A
B
C
D
E
F
1
2
3
4
4.三角形的稳定性
三角形具有稳定性,
四边形没有稳定性.
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状会改变吗 为什么?
不会改变.钉上的木条将四边形分成两个三角形,而三角形具有稳定性.
斜梁
斜梁
直 梁
三角形的稳定性
如图,工人师傅砌门时,常用木条EF,EG固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.
C
E
B
A
F
D
G
三角形的稳定性
1.下列图形中具有稳定性的是( )
A.正方形 B.长方形
C.直角三角形 D.平行四边形
C
2.要使下列木架稳定各至少需要多少根木棍?
答案: 1 2 3
3.你能举例说明三角形的稳定性在实际生活中的应用吗?
三角形的稳定性的应用举例:
(1)自行车的几个梁形成三角支撑;
(2)钢架桥的钢架做成三角形;
(3)起重机的力臂做成三角形;
(4)照相机的支架做成三角形;
(5)高压电线杆的支架做成三角形.
*
三角形的重要线段
高
角平分线
中线
A
B
C
D
A
B
C
D
E
F
G
D
A
C
B
三角形的不稳定性
1.在生产和生活中:①用人字架来建筑房屋;②用窗钩来固
定窗扇;③在栅栏门上斜着定根木条;④商店的推拉活动防盗
门,其中应用了三角形稳定性的有( )
A.1个 B.2个 C.3个 D.4个
解析:①用人字架来建筑房屋应用了三角形稳定性;②
窗钩来固定窗扇应用了三角形稳定性;③在栅栏门上斜着定根木
条应用了三角形稳定性,④商店的推拉活动防盗门应用了四边形
的不稳定性,应用了三角形稳定性的共有3个,故选:C.
C
2. 下列各组图形中,AD是△ABC的高的图形是( )
解析:△ABC的高AD是过顶点A与BC垂直的线段,只有D选
项符合.
D
3.如图,在ΔABC中,AE是中线,
AD是角平分线,AF是高.填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= .
CE
BC
∠CAD
∠BAC
∠AFC
BC AF
4.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是△ABE的角平分线( )
②BE是△ ABD边AD上的中线( )
③BE是△ ABC边AC上的中线( )
④CH是△ ACD边AD上的高( )
三角形的高、中线与角平分线都是线段.
×
×
×
√
理想是指路明星。没有理想,就没有坚定的方向,而没有方向, 就没有生活.
11.1.2 三角形的高、中线与角平分线
11.1.3 三角形的稳定性
你还记得“过一点画已知
直线的垂线”吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
1.理解三角形的高,中线,角平分线等概念.
2.会画三角形的高,中线,角平分线.(重点)
3.了解三角形的稳定性.
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高线,
简称三角形的高。
如图所示, 线段AD是BC边上的高.
任意画一个锐角△ABC,
A
B
C
请你画出BC边上的高.
注意:
标明 垂直的记号和垂足的字母
D
1.三角形的高:
如图所示,△ABC中,AD是△ABC的边BC上的高.
符号语言:
∵ AD是△ ABC的BC边上的高,
∴AD ⊥ BC,
∠ADB=∠ADC=90°.
A
B
C
D
想一想:一个三角形有几条高线?
动手画一画
请画出下列三角形的所有高线,仔细观察,你能得出有什么论?(提示:有几条高,它们是否交于一点?)
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
O
A
B
D
E
F
A
B
C
(D)
●
A
B
C
D
F
E
O
(O)
●
●
C
E
(F)
归纳:1 、锐角三角形的三条高交于内部一点
2、直角三角形的三条高交于直角顶点
3、钝角三角形的三条高所在直线交于外部一点
4、三角形三条高线的交点叫做三角形的垂心.
从三角形的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边上的高.
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
1.下列各组图形中,哪一组图形中的AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
在三角形中,连接一个顶点与它对边中点
的线段,叫做这个三角形的中线.
A
B
C
D
符号语言:
∵AD是△ ABC的 中线
∴BD =CD = BC
1
2
※ 拓展:三角形的中线把它分成面积相等的两个三角形
2.三角形的中线:
请画出下列三角形的所有中线,仔细观察,你能得出有什么论?
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
G
G
G
●
●
●
归纳:
1 、任意三角形的三条中线都在三角形的内部,并且交于一点.
2、三角形三条中线的交点叫做三角形的重心.
A
B
C
D
符号语言:
∵AD是 △ ABC的
角平分线
∴∠ BAD = ∠ CAD
=
1
2
∠BAC
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
思考:三角形的角平分线和角的平分线有什么区别?
3.三角形的角平分线:
三角形的角平分线是一条线段,角的平分线是一条射线.
探究交流
请画出下列三角形的所有角平分线,仔细观察,你能得出有什么论?
归纳:
1 、任意三角形的三条角平分线都在三角形的内部,并且交于一点.
2、三角形三条角平分线的交点叫做三角形的内心.
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
I
I
I
●
●
●
2
2
BD
6 cm
练习1.如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .
A
B
C
D
E
F
G
2.如图,AD,BE,CF 是△ABC 的三条角平分线,则:
∠1 = ;
∠3 = ;
∠ACB = 2 .
∠2
∠ABC
∠4
A
B
C
D
E
F
1
2
3
4
4.三角形的稳定性
三角形具有稳定性,
四边形没有稳定性.
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状会改变吗 为什么?
不会改变.钉上的木条将四边形分成两个三角形,而三角形具有稳定性.
斜梁
斜梁
直 梁
三角形的稳定性
如图,工人师傅砌门时,常用木条EF,EG固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.
C
E
B
A
F
D
G
三角形的稳定性
1.下列图形中具有稳定性的是( )
A.正方形 B.长方形
C.直角三角形 D.平行四边形
C
2.要使下列木架稳定各至少需要多少根木棍?
答案: 1 2 3
3.你能举例说明三角形的稳定性在实际生活中的应用吗?
三角形的稳定性的应用举例:
(1)自行车的几个梁形成三角支撑;
(2)钢架桥的钢架做成三角形;
(3)起重机的力臂做成三角形;
(4)照相机的支架做成三角形;
(5)高压电线杆的支架做成三角形.
*
三角形的重要线段
高
角平分线
中线
A
B
C
D
A
B
C
D
E
F
G
D
A
C
B
三角形的不稳定性
1.在生产和生活中:①用人字架来建筑房屋;②用窗钩来固
定窗扇;③在栅栏门上斜着定根木条;④商店的推拉活动防盗
门,其中应用了三角形稳定性的有( )
A.1个 B.2个 C.3个 D.4个
解析:①用人字架来建筑房屋应用了三角形稳定性;②
窗钩来固定窗扇应用了三角形稳定性;③在栅栏门上斜着定根木
条应用了三角形稳定性,④商店的推拉活动防盗门应用了四边形
的不稳定性,应用了三角形稳定性的共有3个,故选:C.
C
2. 下列各组图形中,AD是△ABC的高的图形是( )
解析:△ABC的高AD是过顶点A与BC垂直的线段,只有D选
项符合.
D
3.如图,在ΔABC中,AE是中线,
AD是角平分线,AF是高.填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= .
CE
BC
∠CAD
∠BAC
∠AFC
BC AF
4.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是△ABE的角平分线( )
②BE是△ ABD边AD上的中线( )
③BE是△ ABC边AC上的中线( )
④CH是△ ACD边AD上的高( )
三角形的高、中线与角平分线都是线段.
×
×
×
√
理想是指路明星。没有理想,就没有坚定的方向,而没有方向, 就没有生活.
