人教版数学八年级上册 12.2三角形全等的判定——第3课时(ASA、AAS) 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.2三角形全等的判定——第3课时(ASA、AAS) 课件(共21张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第3课时
12.2 三角形全等的判定
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.能运用全等三角形的条件,解决简单的推理证明问题.
生活情境
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?
3
2
1
复习巩固:我们已经学习了哪些判定两个三角形全等的方法,它们分别需要哪些条件呢?
AB =A′B′
BC =B′C′
AC =A′C ′
AB =A′B′
∠A=∠A′
AC =A′C ′
A
B
C
A′
B′
C′
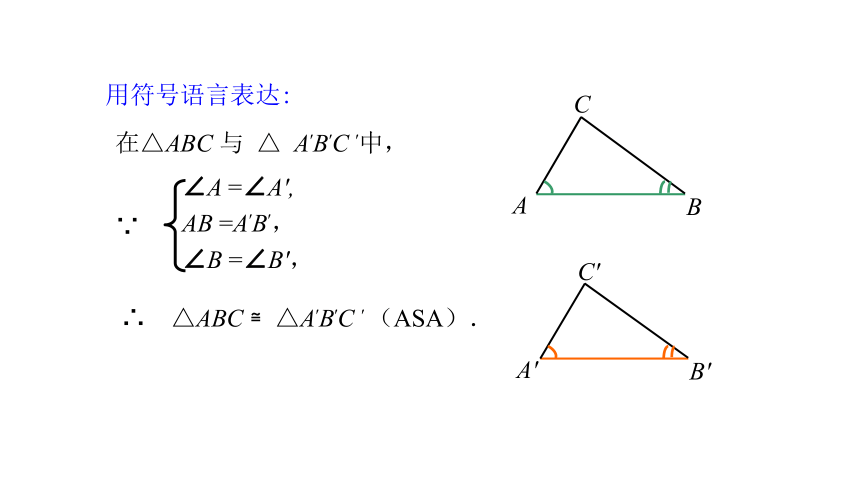
思考:两个角和一条边分别相等的两个三角形是否全等呢?
A
B
C
∠A=∠A′ ∠B=∠B′
A′
B′
C′
A
B
C
A′
B′
C′
AB=A′B′
∠A=∠A′ ∠B=∠B′
BC=B′C′
操作 先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′=AB,∠A′=∠A, ∠B′=∠B .把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
A
B
C
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
条件: A′B′=AB,∠A′=∠A, ∠B′=∠B .
“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等.
(可简写成“角边角”或“ASA”).
A
B
C
A′
B′
C′
用符号语言表达:
在△ABC 与 △ A′B′C ′中,
∴ △ABC ≌△A′B′C ′ (ASA).
∠A =∠A′,
AB =A′B′,
∠B =∠B′,
∵
A
B
C
A′
B′
C′
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:△ABE≌△ACD.
【例题】
证明 :在△ADC和△AEB中,
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知)
∴△ACD≌△ABE(ASA).
思考:如果△ABC和△A′B′C′满足B′C ′ =BC,∠A′ =∠A,∠B′=∠B.△A′B′C′ 和△ABC全等吗?
A
B
C
A′
B′
C′
分析:∠A+∠B+∠C=180°
∠A′+∠B′+∠C ′=180°
||
||
∠C=∠C ′
BC为∠B和∠C的夹边
B′C ′为∠B′和∠C ′的夹边
△ABC ≌△A′B′C ′
A
B
C
A′
B′
C′
解: △ABC ≌△A′B′C ′ .
理由:在△ABC 中,∠A+∠B+∠C=180°.
在△A′B′C′中,∠A′+∠B′+∠C ′=180°.
∵ ∠A=∠A′,∠B=∠B′ ,
∴∠C=∠C ′.
在△ABC 与 △ A′B′C′中,
∠C =∠C ′ ,
BC =B′C ′,
∠B =∠B′,
∵
∴ △ABC ≌△A′B′C ′ (ASA).
条件: BC=B ′ C ′ ,∠A=∠A ′ , ∠B=∠B ′.
“AAS”判定方法:
两角和其中一角的对边分别相等的两个三角形全等.
(可简写成“角角边”或“AAS”).
A
B
C
A′
B′
C′
在△ABC与△A′B′C′ 中,
∠A=∠A′,
∴△ABC≌△A′B′C′(AAS)
A
C
B
A
′
C
B
′
′
∠B=∠B′,
BC=B′C′
用符号语言表达:
1.如图,应填什么就有 △AOC≌ △BOD?
∠A=∠B(已知)
_______(已知)
∠C=∠D(已知)
∴△AOC≌△BOD( )
有几种填法
AC=BD
ASA
【跟踪训练】
如图,应填什么就有△AOC≌△BOD?
∠A=∠B (已知)
________ (已知)
∠C=∠D (已知)
∴△AOC≌△BOD( )
CO=DO
AAS
A
B
C
D
E
F
2.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长.为什么?
提示:利用ASA判定∴△ABC≌△EDC,从而得DE=AB.
A′
B′
C′
“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等.
A
B
C
A′
B′
C′
“AAS”判定方法:
两角和其中一角的对边分别相等的两个三角形全等.
A
B
C
2.判定三角形全等的四种方法,它们分别是:
(1)边边边(SSS) (2)边角边(SAS) (3)角边角(ASA) (4)角角边(AAS)
1. 我们本节课学习了两种新的证明三角形全等的方法:
在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
1.已知,如图,∠1=∠2,∠C=∠D,求证:AC=AD
1
2
【证明】
∠A =∠C,
∠D =∠B ,
AF =CE ,
∴ △ADF ≌△CBE(AAS).
∴ DF =BE.
A
B
C
D
E
F
证明:∵ AD∥CB ,∴ ∠A =∠C.
∵ AE =CF ,∴ AF =CE.
在△ADF 和△CBE 中,
2.如图,E,F 在线段AC上,AD∥CB,AE =CF.若∠B =∠D,求证:DF =BE.
证明:∵ ∠DAB =∠EAC,∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,∴ ∠D =∠E =90°.
在△ADC 和△AEB 中,
A
B
C
D
E
3.如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB
=∠EAC.求证:AB =AC.
∠DAC =∠EAB,
∠D =∠E,
CD =BE,
∴ △ADC ≌△AEB(AAS).
∴ AC =AB.
没有任何问题可以像无穷那样深深地触动人的情感, 很少有别的观念能像无穷那样激励理智产生富有成果的思想, 然而也没有任何其他的概念能像无穷那样需要加以阐明.
——希尔伯特
第3课时
12.2 三角形全等的判定
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.能运用全等三角形的条件,解决简单的推理证明问题.
生活情境
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?
3
2
1
复习巩固:我们已经学习了哪些判定两个三角形全等的方法,它们分别需要哪些条件呢?
AB =A′B′
BC =B′C′
AC =A′C ′
AB =A′B′
∠A=∠A′
AC =A′C ′
A
B
C
A′
B′
C′
思考:两个角和一条边分别相等的两个三角形是否全等呢?
A
B
C
∠A=∠A′ ∠B=∠B′
A′
B′
C′
A
B
C
A′
B′
C′
AB=A′B′
∠A=∠A′ ∠B=∠B′
BC=B′C′
操作 先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′=AB,∠A′=∠A, ∠B′=∠B .把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
A
B
C
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
条件: A′B′=AB,∠A′=∠A, ∠B′=∠B .
“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等.
(可简写成“角边角”或“ASA”).
A
B
C
A′
B′
C′
用符号语言表达:
在△ABC 与 △ A′B′C ′中,
∴ △ABC ≌△A′B′C ′ (ASA).
∠A =∠A′,
AB =A′B′,
∠B =∠B′,
∵
A
B
C
A′
B′
C′
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:△ABE≌△ACD.
【例题】
证明 :在△ADC和△AEB中,
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知)
∴△ACD≌△ABE(ASA).
思考:如果△ABC和△A′B′C′满足B′C ′ =BC,∠A′ =∠A,∠B′=∠B.△A′B′C′ 和△ABC全等吗?
A
B
C
A′
B′
C′
分析:∠A+∠B+∠C=180°
∠A′+∠B′+∠C ′=180°
||
||
∠C=∠C ′
BC为∠B和∠C的夹边
B′C ′为∠B′和∠C ′的夹边
△ABC ≌△A′B′C ′
A
B
C
A′
B′
C′
解: △ABC ≌△A′B′C ′ .
理由:在△ABC 中,∠A+∠B+∠C=180°.
在△A′B′C′中,∠A′+∠B′+∠C ′=180°.
∵ ∠A=∠A′,∠B=∠B′ ,
∴∠C=∠C ′.
在△ABC 与 △ A′B′C′中,
∠C =∠C ′ ,
BC =B′C ′,
∠B =∠B′,
∵
∴ △ABC ≌△A′B′C ′ (ASA).
条件: BC=B ′ C ′ ,∠A=∠A ′ , ∠B=∠B ′.
“AAS”判定方法:
两角和其中一角的对边分别相等的两个三角形全等.
(可简写成“角角边”或“AAS”).
A
B
C
A′
B′
C′
在△ABC与△A′B′C′ 中,
∠A=∠A′,
∴△ABC≌△A′B′C′(AAS)
A
C
B
A
′
C
B
′
′
∠B=∠B′,
BC=B′C′
用符号语言表达:
1.如图,应填什么就有 △AOC≌ △BOD?
∠A=∠B(已知)
_______(已知)
∠C=∠D(已知)
∴△AOC≌△BOD( )
有几种填法
AC=BD
ASA
【跟踪训练】
如图,应填什么就有△AOC≌△BOD?
∠A=∠B (已知)
________ (已知)
∠C=∠D (已知)
∴△AOC≌△BOD( )
CO=DO
AAS
A
B
C
D
E
F
2.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长.为什么?
提示:利用ASA判定∴△ABC≌△EDC,从而得DE=AB.
A′
B′
C′
“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等.
A
B
C
A′
B′
C′
“AAS”判定方法:
两角和其中一角的对边分别相等的两个三角形全等.
A
B
C
2.判定三角形全等的四种方法,它们分别是:
(1)边边边(SSS) (2)边角边(SAS) (3)角边角(ASA) (4)角角边(AAS)
1. 我们本节课学习了两种新的证明三角形全等的方法:
在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D (已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
1.已知,如图,∠1=∠2,∠C=∠D,求证:AC=AD
1
2
【证明】
∠A =∠C,
∠D =∠B ,
AF =CE ,
∴ △ADF ≌△CBE(AAS).
∴ DF =BE.
A
B
C
D
E
F
证明:∵ AD∥CB ,∴ ∠A =∠C.
∵ AE =CF ,∴ AF =CE.
在△ADF 和△CBE 中,
2.如图,E,F 在线段AC上,AD∥CB,AE =CF.若∠B =∠D,求证:DF =BE.
证明:∵ ∠DAB =∠EAC,∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,∴ ∠D =∠E =90°.
在△ADC 和△AEB 中,
A
B
C
D
E
3.如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB
=∠EAC.求证:AB =AC.
∠DAC =∠EAB,
∠D =∠E,
CD =BE,
∴ △ADC ≌△AEB(AAS).
∴ AC =AB.
没有任何问题可以像无穷那样深深地触动人的情感, 很少有别的观念能像无穷那样激励理智产生富有成果的思想, 然而也没有任何其他的概念能像无穷那样需要加以阐明.
——希尔伯特
