人教版数学八年级上册 12.2三角形全等的判定——第4课时(HL) 课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.2三角形全等的判定——第4课时(HL) 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 800.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 08:51:55 | ||
图片预览





文档简介
(共19张PPT)
12.2 三角形全等的判定
第4课时 HL
学习目标:
1.探索并掌握判定直角三角形全等的“斜边、直角边” 方法.
2.能利用“斜边、直角边”方法判定两个直角三角形全等.
3.能选择适当的判定方法证明两个三角形全等.
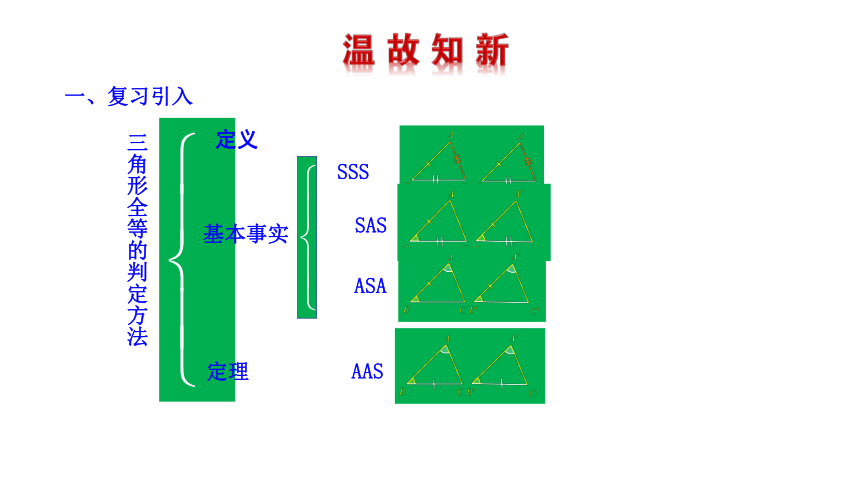
SAS
SSS
三角形全等的判定方法
基本事实
定理
ASA
定义
AAS
一、复习引入
操作 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
A
B
C
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
条件:∠C=∠C′=90°,B′C′=BC,A′B′=AB
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等
(简写为“斜边、直角边”或“HL”).
N
M
C′
A
B
C
A′
B′
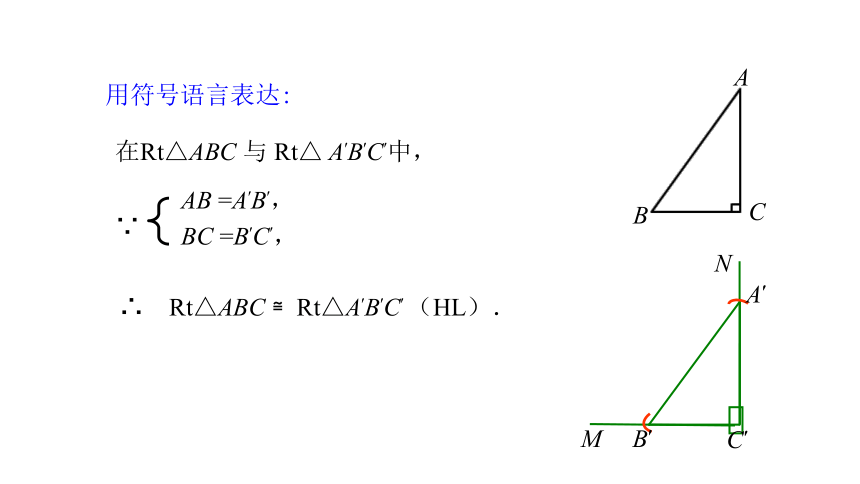
用符号语言表达:
在Rt△ABC 与 Rt△ A′B′C′中,
∴ Rt△ABC ≌Rt△A′B′C′ (HL).
AB =A′B′,
BC =B′C′,
∵
N
M
C′
A
B
C
A′
B′
想一想 议一议
你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
例1如图,AC⊥BC,BD⊥AD,AC﹦BD,求证:BC﹦AD。
证明:∵AC⊥BC,BD⊥AD,
∴∠C与∠D都是直角。
AB=BA,
AC=BD。
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL)。
∴BC﹦AD(全等三角形的对应边相等)。
应用“HL”的前提条件是在直角三角形中。
这是应用“HL”判定方法的书写格式。
利用全等证明两条线段相等,这是常见的思路。
典例解析
A
B
C
D
例2 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
【解析】在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
A
F
C
E
D
B
1.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.
【跟踪训练】
【证明】在Rt△ABF和Rt△CDE中,
∵AE=CF,
∴AF=CE.
又∵AB=CD,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
A
B
C
D
E
F
2. 如图,两根长度为12 m的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
BD=CD.
∵∠ADB=∠ADC=90°,
AB=AC
AD=AD
∴Rt△ABD≌Rt△ACD(HL),
∴ BD=CD.
【解析】
通过本课时的学习,需要我们掌握:
直角三角形是特殊的三角形,所以不仅有一般三角形
判定全等的方法: SSS、SAS、ASA、AAS,还有直角三角形
特殊的判定方法:HL.
1.(2020·黑龙江中考)如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个
条件 ,使Rt△ABC和Rt△EDF全等.
AB=ED(BC=DF或
AC=EF或AE=CF)
2.如图,AC,BD是长方形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【解析】在长方形ABCD中,△CDA、△BAD、△DCB都和△ABC全等,∠ABC=∠DCE=90°,DE∥AC,所以∠DEC=∠ACB;又AB=DC,所以△DCE也和△ABC全等.
D
3.如图,AC⊥BC,BD⊥AD,要证△ABC ≌△BAD,
需要添加一个什么条件?请说明理由.
A
B
C
D
(1)AD = BC 理由:HL
(2)AC = BD 理由:HL
(3)∠DBA = ∠CAB 理由:AAS
(4)∠DAB = ∠CBA 理由:AAS
4. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
在Rt△ACB和Rt△ADB中,
AB=AB,
AC=AD,
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD.
(全等三角形对应边相等).
【解析】
勤奋工作,勇于实践;始终坚持学习;
做一个有德行的人;富有创新精神。
—— 富兰克林
12.2 三角形全等的判定
第4课时 HL
学习目标:
1.探索并掌握判定直角三角形全等的“斜边、直角边” 方法.
2.能利用“斜边、直角边”方法判定两个直角三角形全等.
3.能选择适当的判定方法证明两个三角形全等.
SAS
SSS
三角形全等的判定方法
基本事实
定理
ASA
定义
AAS
一、复习引入
操作 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
A
B
C
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
条件:∠C=∠C′=90°,B′C′=BC,A′B′=AB
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等
(简写为“斜边、直角边”或“HL”).
N
M
C′
A
B
C
A′
B′
用符号语言表达:
在Rt△ABC 与 Rt△ A′B′C′中,
∴ Rt△ABC ≌Rt△A′B′C′ (HL).
AB =A′B′,
BC =B′C′,
∵
N
M
C′
A
B
C
A′
B′
想一想 议一议
你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
例1如图,AC⊥BC,BD⊥AD,AC﹦BD,求证:BC﹦AD。
证明:∵AC⊥BC,BD⊥AD,
∴∠C与∠D都是直角。
AB=BA,
AC=BD。
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL)。
∴BC﹦AD(全等三角形的对应边相等)。
应用“HL”的前提条件是在直角三角形中。
这是应用“HL”判定方法的书写格式。
利用全等证明两条线段相等,这是常见的思路。
典例解析
A
B
C
D
例2 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
【解析】在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠ABC=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
A
F
C
E
D
B
1.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.
【跟踪训练】
【证明】在Rt△ABF和Rt△CDE中,
∵AE=CF,
∴AF=CE.
又∵AB=CD,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
A
B
C
D
E
F
2. 如图,两根长度为12 m的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
BD=CD.
∵∠ADB=∠ADC=90°,
AB=AC
AD=AD
∴Rt△ABD≌Rt△ACD(HL),
∴ BD=CD.
【解析】
通过本课时的学习,需要我们掌握:
直角三角形是特殊的三角形,所以不仅有一般三角形
判定全等的方法: SSS、SAS、ASA、AAS,还有直角三角形
特殊的判定方法:HL.
1.(2020·黑龙江中考)如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个
条件 ,使Rt△ABC和Rt△EDF全等.
AB=ED(BC=DF或
AC=EF或AE=CF)
2.如图,AC,BD是长方形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【解析】在长方形ABCD中,△CDA、△BAD、△DCB都和△ABC全等,∠ABC=∠DCE=90°,DE∥AC,所以∠DEC=∠ACB;又AB=DC,所以△DCE也和△ABC全等.
D
3.如图,AC⊥BC,BD⊥AD,要证△ABC ≌△BAD,
需要添加一个什么条件?请说明理由.
A
B
C
D
(1)AD = BC 理由:HL
(2)AC = BD 理由:HL
(3)∠DBA = ∠CAB 理由:AAS
(4)∠DAB = ∠CBA 理由:AAS
4. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
在Rt△ACB和Rt△ADB中,
AB=AB,
AC=AD,
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD.
(全等三角形对应边相等).
【解析】
勤奋工作,勇于实践;始终坚持学习;
做一个有德行的人;富有创新精神。
—— 富兰克林
