人教版 数学八年级上册 12.3 角的平分线的性质 课件(共27张PPT)
文档属性
| 名称 | 人教版 数学八年级上册 12.3 角的平分线的性质 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 08:53:44 | ||
图片预览



文档简介
(共27张PPT)
12.3 角的平分线的性质
1.角平分线的概念
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线.
o
B
C
A
1
2
温故知新
2.点到直线距离
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离.
O
P
A
B
线段的长度
复习提问
1.在探究作角平分线的方法和角平分线性质的过程中,掌握角平分线的作法和角平分线的性质.
2.提高综合运用三角形全等的有关知识解决问题的能力;掌握简单的角平分线在生产、生活中的应用.
不利用工具,请你将一张用纸片做的角分成两个相等的角.你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
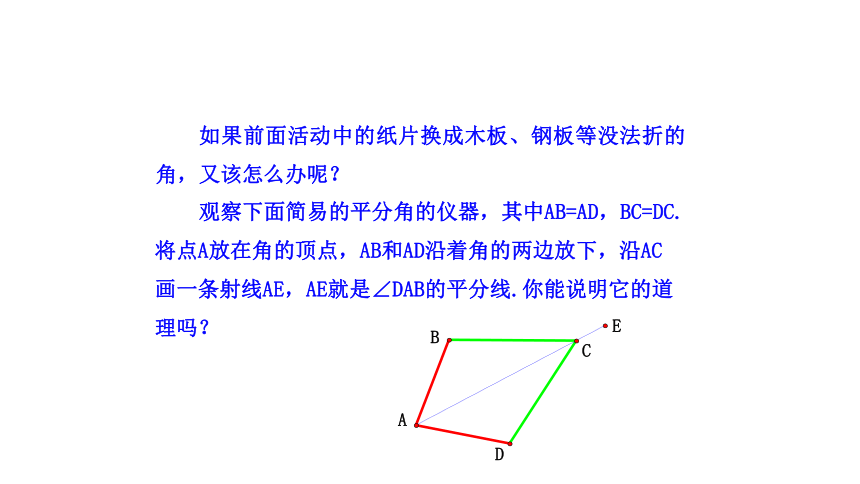
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
观察下面简易的平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线.你能说明它的道理吗?
B
D
A
C
E
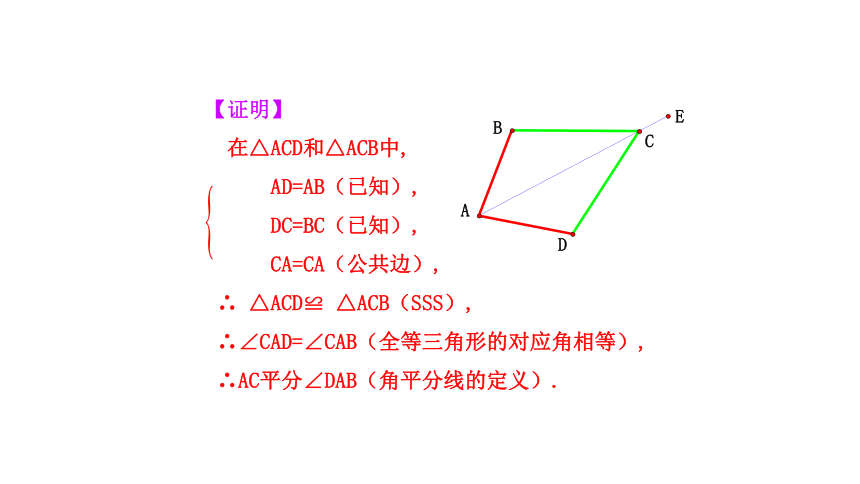
【证明】
在△ACD和△ACB中,
AD=AB(已知),
DC=BC(已知),
CA=CA(公共边),
∴ △ACD≌ △ACB(SSS),
∴∠CAD=∠CAB(全等三角形的对应角相等),
∴AC平分∠DAB(角平分线的定义).
B
D
A
C
E
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
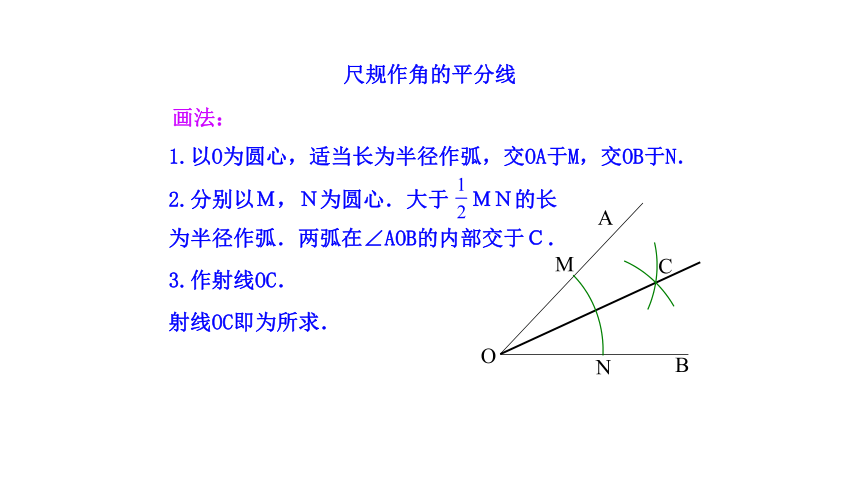
尺规作角的平分线
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
O
A
B
N
M
C
证明:连接MC,NC由作法知:
在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴△OMC≌△ONC(SSS),
∴∠AOC=∠BOC,
即OC 是∠AOB的平分线.
为什么OC是∠AOB的平分线
O
A
B
N
M
C
猜想:角的平分线上的点到角的两边的距离相等.
将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
证明:∵ OC平分∠AOB, P是OC上一点(已知),
∴∠DOP=∠BOP(角平分线定义).
∵PD⊥OA,PE⊥OB (已知),
∴∠ODP=∠OEP=90°(垂直的定义).
在△OPD和△OPE中
∠DOP=∠BOP (已证),
∠ODP=∠OEP (已证),
OP=OP (已知),
∴ △OPD≌△OPE(AAS),
∴PD=PE(全等三角形对应边相等).
已知:OC平分∠AOB,点P在OC上,PD⊥OA于D,
PE⊥OB于E,
求证: PD=PE.
P
A
O
B
C
E
D
1
2
定理:角的平分线上的点到角的两边的距离相等.
用符号语言表示为:
∵∠1= ∠2,
PD ⊥OA ,PE ⊥OB,
∴PD=PE.
P
A
O
B
C
E
D
1
2
角的平分线的性质
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500 m,这个集贸市场应建在何处?(比例尺为1︰20 000)
s
【跟踪训练】
解: 设OD=Xm, 则由题得 = , 解得x=0.025m, 即OD=2.5cm.
作夹角的角平分线OC,截取 OD=2.5cm ,D即为所求.
D
C
s
公路
铁路
O
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
反过来,角的内部到角的两边的距离相等的点是否一定在这个角的平分线上呢?
证明: ∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义) 在Rt△QDO和Rt△QEO中
QO=QO(公共边) QD=QE ∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠ QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
判定:角的内部到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE
∴点Q在∠AOB的平分线上.
用数学语言表示为:
例 如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足分别为D、E、F.
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、 CA的距离相等
A
B
C
M
N
P
D
E
F
怎样找三角形内到三角形三边距离相等的点?
(1)∵∠1= ∠2,DC⊥AC, DE⊥AB,
∴___________.
(________________________________________)
(2)∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(________________________________________________)
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
角的内部到角的两边的距离相等的点在角的平分线上.
角的平分线上的点到角的两边的距离相等
【跟踪训练】
2.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.
求证:点P到三边AB,BC,CA所在直线的距离相等.
A
B
C
D
E
P
F
G
H
B
P
更上一层楼!
1.角的内部到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
2.角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
用数学语言表示为:
本节主要内容
1.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.
B
A
E
D
C
F
【解析】根据角的平分线的性质得DE=DF,再根据HL证明△BED≌△CFD,从而得到EB=FC.
【证明】∵AD是△ABC的角平分线,DE⊥AB、DF⊥AC,∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△DFC中,
,
∴Rt△BED≌Rt△CFD(HL),
∴EB=FC.
2.直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B.两处 C.三处 D.四处
【解析】由于没有限制在何处选址,故要求的地址共有四处,在各自夹角的平分线上,即:A、B、C、D各一处.
A
D
C
B
D
3.如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明.
B D
A
E
F
c
【解析】解法一:添加条件:AE=AF.
在△AED与△AFD中,
∵AE=AF,∠EAD=∠FAD,AD=AD,
∴△AED≌△AFD(SAS).
解法二:添加条件:∠EDA=∠FDA.
在△AED与△AFD中,
∵∠EAD=∠FAD,AD=AD,∠EDA=∠FDA,
∴△AED≌△AFD(ASA).
时间是个常数,但对勤奋者来说,是个“变数”.用“分”来计算时间的人比用“小时”来计算时间的人时间多59倍.
——雷巴柯夫
12.3 角的平分线的性质
1.角平分线的概念
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线.
o
B
C
A
1
2
温故知新
2.点到直线距离
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离.
O
P
A
B
线段的长度
复习提问
1.在探究作角平分线的方法和角平分线性质的过程中,掌握角平分线的作法和角平分线的性质.
2.提高综合运用三角形全等的有关知识解决问题的能力;掌握简单的角平分线在生产、生活中的应用.
不利用工具,请你将一张用纸片做的角分成两个相等的角.你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
观察下面简易的平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线.你能说明它的道理吗?
B
D
A
C
E
【证明】
在△ACD和△ACB中,
AD=AB(已知),
DC=BC(已知),
CA=CA(公共边),
∴ △ACD≌ △ACB(SSS),
∴∠CAD=∠CAB(全等三角形的对应角相等),
∴AC平分∠DAB(角平分线的定义).
B
D
A
C
E
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
尺规作角的平分线
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
O
A
B
N
M
C
证明:连接MC,NC由作法知:
在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴△OMC≌△ONC(SSS),
∴∠AOC=∠BOC,
即OC 是∠AOB的平分线.
为什么OC是∠AOB的平分线
O
A
B
N
M
C
猜想:角的平分线上的点到角的两边的距离相等.
将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
证明:∵ OC平分∠AOB, P是OC上一点(已知),
∴∠DOP=∠BOP(角平分线定义).
∵PD⊥OA,PE⊥OB (已知),
∴∠ODP=∠OEP=90°(垂直的定义).
在△OPD和△OPE中
∠DOP=∠BOP (已证),
∠ODP=∠OEP (已证),
OP=OP (已知),
∴ △OPD≌△OPE(AAS),
∴PD=PE(全等三角形对应边相等).
已知:OC平分∠AOB,点P在OC上,PD⊥OA于D,
PE⊥OB于E,
求证: PD=PE.
P
A
O
B
C
E
D
1
2
定理:角的平分线上的点到角的两边的距离相等.
用符号语言表示为:
∵∠1= ∠2,
PD ⊥OA ,PE ⊥OB,
∴PD=PE.
P
A
O
B
C
E
D
1
2
角的平分线的性质
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500 m,这个集贸市场应建在何处?(比例尺为1︰20 000)
s
【跟踪训练】
解: 设OD=Xm, 则由题得 = , 解得x=0.025m, 即OD=2.5cm.
作夹角的角平分线OC,截取 OD=2.5cm ,D即为所求.
D
C
s
公路
铁路
O
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
反过来,角的内部到角的两边的距离相等的点是否一定在这个角的平分线上呢?
证明: ∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义) 在Rt△QDO和Rt△QEO中
QO=QO(公共边) QD=QE ∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠ QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
判定:角的内部到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE
∴点Q在∠AOB的平分线上.
用数学语言表示为:
例 如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足分别为D、E、F.
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、 CA的距离相等
A
B
C
M
N
P
D
E
F
怎样找三角形内到三角形三边距离相等的点?
(1)∵∠1= ∠2,DC⊥AC, DE⊥AB,
∴___________.
(________________________________________)
(2)∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(________________________________________________)
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
角的内部到角的两边的距离相等的点在角的平分线上.
角的平分线上的点到角的两边的距离相等
【跟踪训练】
2.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.
求证:点P到三边AB,BC,CA所在直线的距离相等.
A
B
C
D
E
P
F
G
H
B
P
更上一层楼!
1.角的内部到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
2.角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
用数学语言表示为:
本节主要内容
1.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.
B
A
E
D
C
F
【解析】根据角的平分线的性质得DE=DF,再根据HL证明△BED≌△CFD,从而得到EB=FC.
【证明】∵AD是△ABC的角平分线,DE⊥AB、DF⊥AC,∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△DFC中,
,
∴Rt△BED≌Rt△CFD(HL),
∴EB=FC.
2.直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B.两处 C.三处 D.四处
【解析】由于没有限制在何处选址,故要求的地址共有四处,在各自夹角的平分线上,即:A、B、C、D各一处.
A
D
C
B
D
3.如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明.
B D
A
E
F
c
【解析】解法一:添加条件:AE=AF.
在△AED与△AFD中,
∵AE=AF,∠EAD=∠FAD,AD=AD,
∴△AED≌△AFD(SAS).
解法二:添加条件:∠EDA=∠FDA.
在△AED与△AFD中,
∵∠EAD=∠FAD,AD=AD,∠EDA=∠FDA,
∴△AED≌△AFD(ASA).
时间是个常数,但对勤奋者来说,是个“变数”.用“分”来计算时间的人比用“小时”来计算时间的人时间多59倍.
——雷巴柯夫
