人教版 数学八年级上册 13.1.2 线段的垂直平分线的性质 课件(共34张PPT)
文档属性
| 名称 | 人教版 数学八年级上册 13.1.2 线段的垂直平分线的性质 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 08:55:27 | ||
图片预览









文档简介
(共34张PPT)
第十三章 轴对称
13.1 轴对称
13.1.2 线段的垂直平分线的性质
如果一个平面图形沿一条直线 ,直线两旁的部分能够 ,这个图形就叫做轴对称图形.
折痕所在的这条直线叫做_________.
对称轴
折叠
互相重合
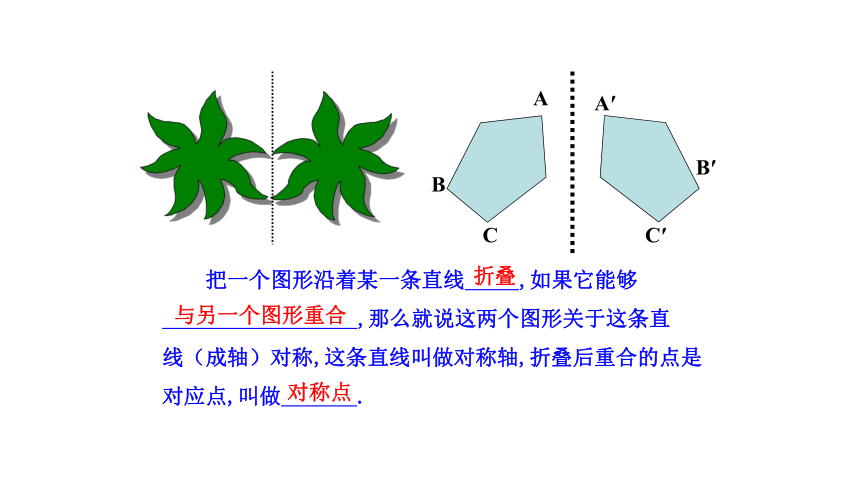
把一个图形沿着某一条直线 ,如果它能够
,那么就说这两个图形关于这条直
线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 .
A′
A
B
C
B′
C′
折叠
与另一个图形重合
对称点
1.了解轴对称及线段垂直平分线的性质和判定.
2.会应用线段垂直平分线的性质和判定解题.
3.依据轴对称的性质找出两个图形成轴对称及轴对称图形的对称轴.
4.作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
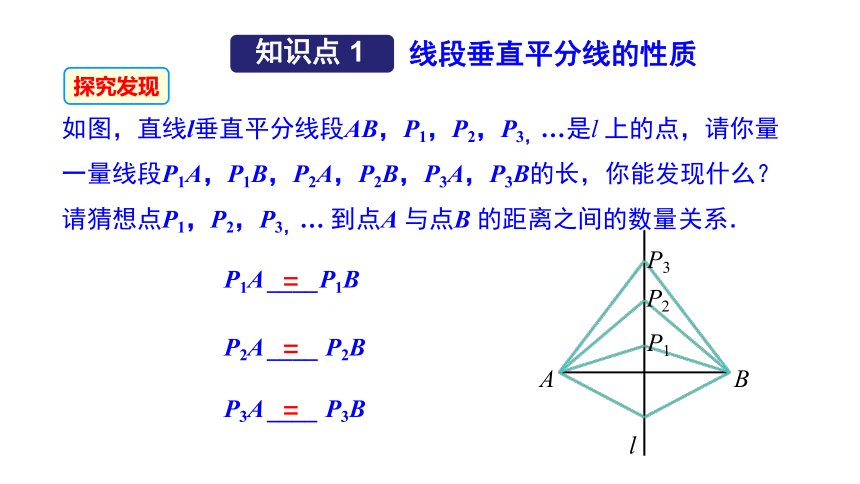
P2A ____ P2B
如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A ____P1B
P3A ____ P3B
=
=
=
线段垂直平分线的性质
知识点 1
探究发现
=
=
=
猜想:
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
验证结论
例1 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm B.10cm C.15cm D.17.5cm
C
解析:∵△DBC的周长为BC+BD+CD=35cm,又∵DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).
典例解析
利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
方法归纳:
A
B
C
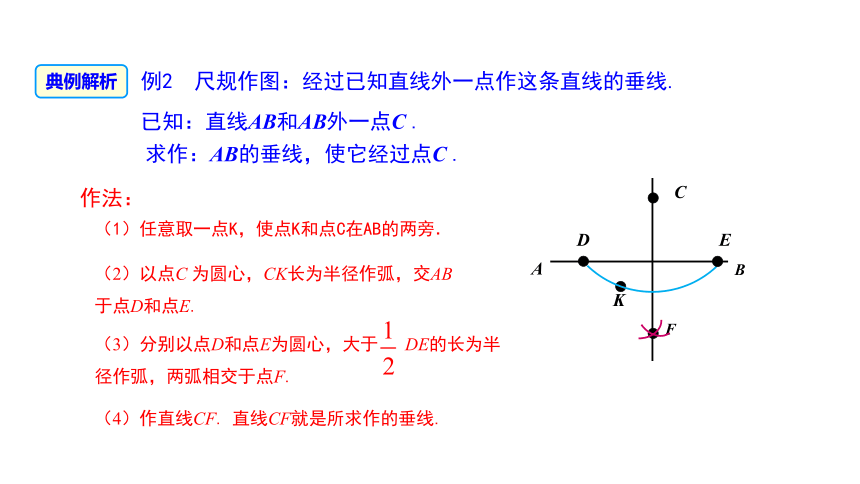
例2 尺规作图:经过已知直线外一点作这条直线的垂线.
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
F
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
作法:
典例解析
(1)为什么任意取一点K ,使点K与点C 在直线两旁?
(2)为什么要以大于 的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
想一想:
例3 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
解析:
典例解析
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
现在你能想到方法确定购物中心的位置,使得它到三个小区的距离相等吗?
例4 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可得出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)先根据线段垂直平分线的性质得出AB=BF,再结合(1)即可解答.
证明:(1)∵AD∥BC,
∴∠ADC=∠ECF.
∵E是CD的中点,
∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
跟踪训练
3.如图,在△ABC 中,BC =8,AB的中垂线交BC于D,AC的
中垂线交BC于E,则△ADE 的周长等于______.
8
A
B
C
D
E
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
合作探究
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
线段垂直平分线的判定
知识点 3
证明:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
知识要点
线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
这些点能组成什么几何图形?
你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB 两端点距离相等的点?
与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与A、B两点 的距离相等的所有点的集合.
P
A
B
C
l
应用格式:
∵ AB =AC,MB =MC,
∴ 直线AM 是线段BC 的垂直平分线.
A
B
C
D
M
这是判断一条直线是线段的垂直平分线的方法.
例5 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
典例解析
跟踪训练
1.如图所示,AC=AD,BC=BD,则下列说法正确的是 ( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
A
2.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
如何作出线段的垂直平分线?
由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端点距离相等的两点并连接即可.
线段垂直平分线的作法
知识点 3
问题引入
作线段的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
A
B
C
D
作法:
(2)作直线CD.CD即为所求.
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
1.下图中的五角星有几条对称轴?作出这些对称轴.
A
B
作法:(1)找出五角星的一对对应点A和B,连接AB.
(2)作出线段AB的垂直平分线n.
则n就是这个五角星的一条对称轴.
n
用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴.
跟踪训练
2.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
【提示】连接AB,作AB的垂直平分线,则与公路的交点就是要建的公共汽车站.
线段的垂直平分线
性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
集合
定义
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
关系
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
1.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
2.如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.
7.8
3. 如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 __________ 的垂直平分线上.
AC
解析:∵BC=BD+AD,
又∵BC=BD+DC,
∴AD=DC.
∴点D在线段AC的垂直平分线上.
4. 有A,B,C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置.
A
B
C
【提示】学校在连接任意两点的两条线段的垂直平分线的交点处.
在数学的领域中,提出问题的艺术比解答问题的艺术更为重要.
——康托尔
第十三章 轴对称
13.1 轴对称
13.1.2 线段的垂直平分线的性质
如果一个平面图形沿一条直线 ,直线两旁的部分能够 ,这个图形就叫做轴对称图形.
折痕所在的这条直线叫做_________.
对称轴
折叠
互相重合
把一个图形沿着某一条直线 ,如果它能够
,那么就说这两个图形关于这条直
线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 .
A′
A
B
C
B′
C′
折叠
与另一个图形重合
对称点
1.了解轴对称及线段垂直平分线的性质和判定.
2.会应用线段垂直平分线的性质和判定解题.
3.依据轴对称的性质找出两个图形成轴对称及轴对称图形的对称轴.
4.作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
P2A ____ P2B
如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A ____P1B
P3A ____ P3B
=
=
=
线段垂直平分线的性质
知识点 1
探究发现
=
=
=
猜想:
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
验证结论
例1 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm B.10cm C.15cm D.17.5cm
C
解析:∵△DBC的周长为BC+BD+CD=35cm,又∵DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).
典例解析
利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
方法归纳:
A
B
C
例2 尺规作图:经过已知直线外一点作这条直线的垂线.
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
F
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
作法:
典例解析
(1)为什么任意取一点K ,使点K与点C 在直线两旁?
(2)为什么要以大于 的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
想一想:
例3 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
解析:
典例解析
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
现在你能想到方法确定购物中心的位置,使得它到三个小区的距离相等吗?
例4 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可得出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)先根据线段垂直平分线的性质得出AB=BF,再结合(1)即可解答.
证明:(1)∵AD∥BC,
∴∠ADC=∠ECF.
∵E是CD的中点,
∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
跟踪训练
3.如图,在△ABC 中,BC =8,AB的中垂线交BC于D,AC的
中垂线交BC于E,则△ADE 的周长等于______.
8
A
B
C
D
E
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
合作探究
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
线段垂直平分线的判定
知识点 3
证明:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
知识要点
线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
这些点能组成什么几何图形?
你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB 两端点距离相等的点?
与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与A、B两点 的距离相等的所有点的集合.
P
A
B
C
l
应用格式:
∵ AB =AC,MB =MC,
∴ 直线AM 是线段BC 的垂直平分线.
A
B
C
D
M
这是判断一条直线是线段的垂直平分线的方法.
例5 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
典例解析
跟踪训练
1.如图所示,AC=AD,BC=BD,则下列说法正确的是 ( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
A
2.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
如何作出线段的垂直平分线?
由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端点距离相等的两点并连接即可.
线段垂直平分线的作法
知识点 3
问题引入
作线段的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
A
B
C
D
作法:
(2)作直线CD.CD即为所求.
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
1.下图中的五角星有几条对称轴?作出这些对称轴.
A
B
作法:(1)找出五角星的一对对应点A和B,连接AB.
(2)作出线段AB的垂直平分线n.
则n就是这个五角星的一条对称轴.
n
用同样的方法,可以找出五条对称轴,所以五角星有五条对称轴.
跟踪训练
2.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
【提示】连接AB,作AB的垂直平分线,则与公路的交点就是要建的公共汽车站.
线段的垂直平分线
性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
集合
定义
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
关系
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
1.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
2.如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.
7.8
3. 如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 __________ 的垂直平分线上.
AC
解析:∵BC=BD+AD,
又∵BC=BD+DC,
∴AD=DC.
∴点D在线段AC的垂直平分线上.
4. 有A,B,C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置.
A
B
C
【提示】学校在连接任意两点的两条线段的垂直平分线的交点处.
在数学的领域中,提出问题的艺术比解答问题的艺术更为重要.
——康托尔
