人教版数学八年级上册 13.3.1 等腰三角形(第1课时) 课件(共31张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1 等腰三角形(第1课时) 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 09:00:05 | ||
图片预览








文档简介
(共31张PPT)
第1课时
13.3 等腰三角形
13.3.1 等腰三角形
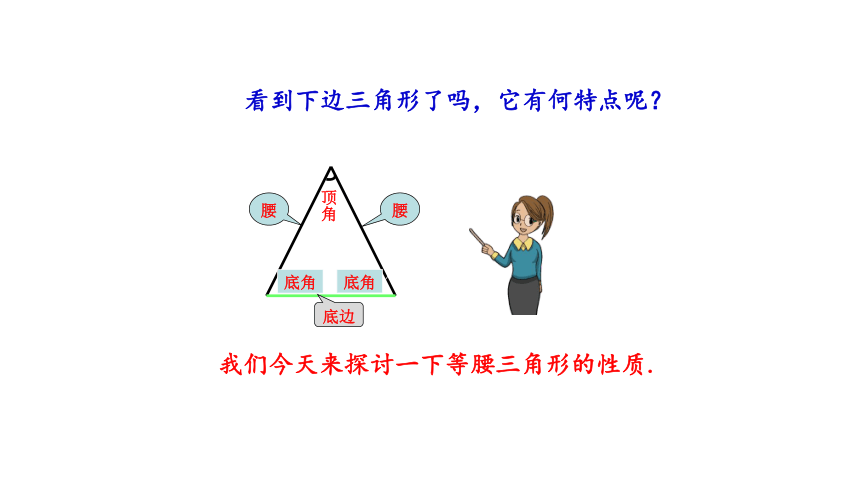
看到下边三角形了吗,它有何特点呢?
腰
腰
顶角
底角
底角
底边
我们今天来探讨一下等腰三角形的性质.
1.了解等腰三角形的概念,掌握等腰三角形的性质;
2.运用等腰三角形的概念及性质解决相关问题.
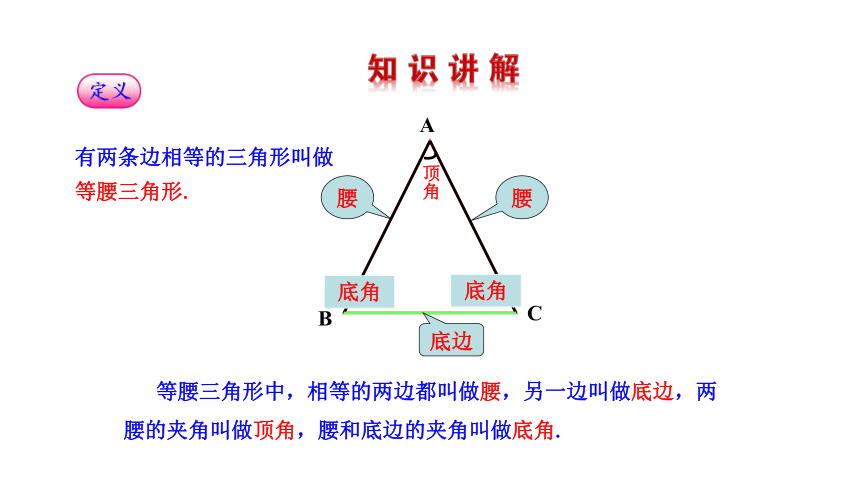
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点?
互动探究
等腰三角形的性质1
知识点 1
A
B
C
AB=AC
等腰三角形
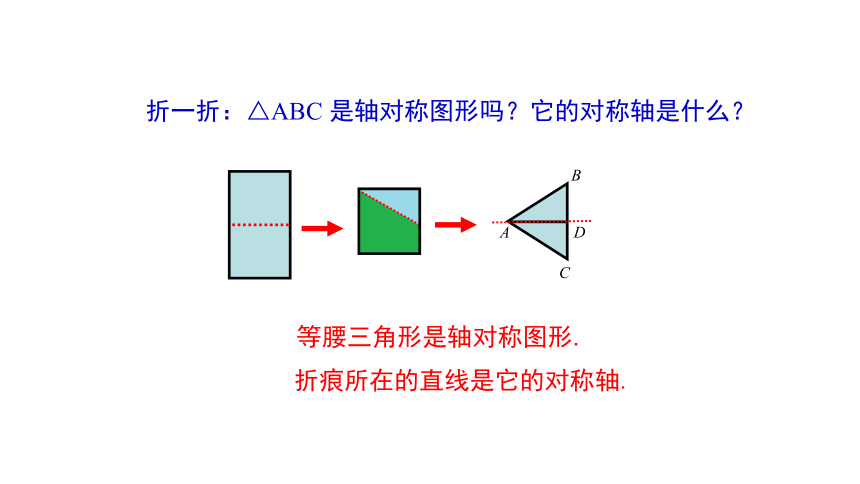
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
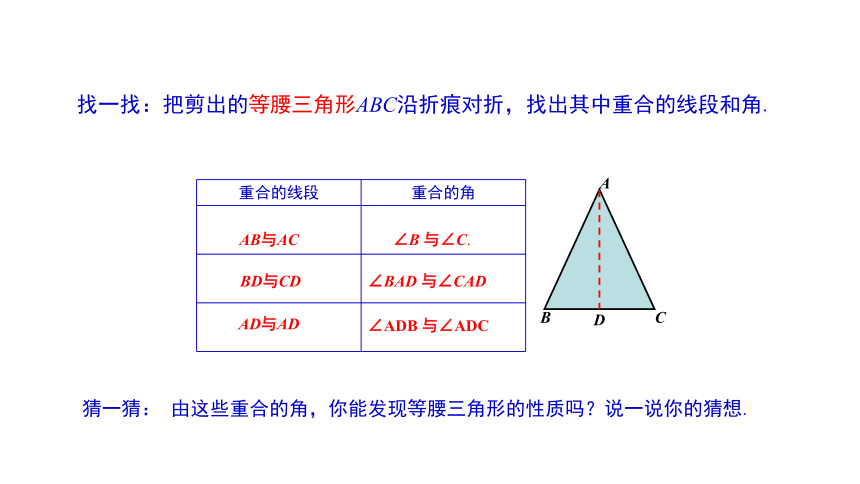
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜: 由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
性质1 等腰三角形的两个底角相等(等边对等角).
A
B
C
D
猜想与验证
已知:△ABC 中,AB=AC .
求证:∠B=∠C.
证法1:作底边BC边上的中线AD.
在△ABD与△ACD中,
AB=AC(已知),
BD=DC(作图),
AD=AD(公共边),
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形对应角相等)
应用格式:
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
证法2:作顶角∠BAC的平分线AD,交BC于点D.
∵AD平分∠BAC ,
∴∠1=∠2.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
∴ △ABD ≌ △ACD(SAS),
∴ ∠B=∠C.
A
B
C
D
(
(
1
2
证法3:
证明:作底边BC的高AD,交BC于点D.
∵AD⊥BC,
∴ ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
∴ Rt△ABD ≌ Rt△ACD(HL),
∴ ∠B=∠C.
A
B
C
D
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
典例解析
分析:(1)观察∠BDC与∠A、∠ABD的关系,∠BDC与∠C、∠ABC呢?
∠BDC= ∠A+ ∠ABD=2 ∠A,
∠ABC= ∠C= ∠BDC=2 ∠A.
(2)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠ C=180 °
∴x+2x+2x=180 °,
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
∴∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
方法总结:利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:∵AB=AD=DC
∴ ∠B= ∠ADB,∠C= ∠DAC.
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x,
在△ABC中, 根据三角形内角和定理,得
2x+x+26°+x=180°,
解得x=38.5°.
∴ ∠C= x=38.5°, ∠B=2x=77°.
跟踪训练
例2 等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40° C.65°或80° D.50°或80°
解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
A
典例解析
方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
跟踪训练
1.等腰三角形一个底角为75°,它的另外两个角为_______;
2.等腰三角形一个角为70°,它的另外两个角为___________________;
3.等腰三角形一个角为110°,它的另外两个角为________。
75°, 30°
70°,40°或55°,55°
35°,35°
由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到哪些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
想一想
探究新知
性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
即:等腰三角形
顶角平分线
底边上的高线
底边上的中线
具备其中一条
另外两条成立
归纳总结
A
C
B
D
1
2
∵AB=AC, ∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一)
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一)
∵AB=AC, AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一)
综上可得:如图,在△ABC中,
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合
思考:
为什么不一样?
例3 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
典例解析
图②
图①
证明:(1)如图①,过A作
AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图①
G
方法总结:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
图②
如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
跟踪训练
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线和底边上的高互相
重合,简称“三线合 一”
分类讨论思想的应用
轴对称图形
等腰三角形的性质
2.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
1.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
3.在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
A
B
C
A
B
C
70°或20°
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
4.如图,在△ABC中,AB = AC,D是BC边上的中点,∠B = 30°,求 ∠BAD 和 ∠ADC的度数.
A
B
C
D
解:∵AB=AC,D是BC边上的中点,
∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°.
∴∠ BAC =180° - 30°-30° = 120°.
∴ = 60°.
5.如图,已知△ABC为等腰三角形,BD、CE分别为底角的平分线,且∠DBC=∠F,求证:EC∥DF.
∴∠DBC=∠ECB.
∵∠DBC=∠F,∴∠ECB=∠F,∴EC∥DF.
证明:∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
又∵BD、CE分别为底角的平分线,
∴
如果命运是块顽石,我就化为大锤,将它砸得粉碎!
——欧拉
第1课时
13.3 等腰三角形
13.3.1 等腰三角形
看到下边三角形了吗,它有何特点呢?
腰
腰
顶角
底角
底角
底边
我们今天来探讨一下等腰三角形的性质.
1.了解等腰三角形的概念,掌握等腰三角形的性质;
2.运用等腰三角形的概念及性质解决相关问题.
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点?
互动探究
等腰三角形的性质1
知识点 1
A
B
C
AB=AC
等腰三角形
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜: 由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
性质1 等腰三角形的两个底角相等(等边对等角).
A
B
C
D
猜想与验证
已知:△ABC 中,AB=AC .
求证:∠B=∠C.
证法1:作底边BC边上的中线AD.
在△ABD与△ACD中,
AB=AC(已知),
BD=DC(作图),
AD=AD(公共边),
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形对应角相等)
应用格式:
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
证法2:作顶角∠BAC的平分线AD,交BC于点D.
∵AD平分∠BAC ,
∴∠1=∠2.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
∴ △ABD ≌ △ACD(SAS),
∴ ∠B=∠C.
A
B
C
D
(
(
1
2
证法3:
证明:作底边BC的高AD,交BC于点D.
∵AD⊥BC,
∴ ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
∴ Rt△ABD ≌ Rt△ACD(HL),
∴ ∠B=∠C.
A
B
C
D
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
典例解析
分析:(1)观察∠BDC与∠A、∠ABD的关系,∠BDC与∠C、∠ABC呢?
∠BDC= ∠A+ ∠ABD=2 ∠A,
∠ABC= ∠C= ∠BDC=2 ∠A.
(2)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠ C=180 °
∴x+2x+2x=180 °,
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
∴∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
方法总结:利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:∵AB=AD=DC
∴ ∠B= ∠ADB,∠C= ∠DAC.
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x,
在△ABC中, 根据三角形内角和定理,得
2x+x+26°+x=180°,
解得x=38.5°.
∴ ∠C= x=38.5°, ∠B=2x=77°.
跟踪训练
例2 等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40° C.65°或80° D.50°或80°
解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
A
典例解析
方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
跟踪训练
1.等腰三角形一个底角为75°,它的另外两个角为_______;
2.等腰三角形一个角为70°,它的另外两个角为___________________;
3.等腰三角形一个角为110°,它的另外两个角为________。
75°, 30°
70°,40°或55°,55°
35°,35°
由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到哪些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
想一想
探究新知
性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
即:等腰三角形
顶角平分线
底边上的高线
底边上的中线
具备其中一条
另外两条成立
归纳总结
A
C
B
D
1
2
∵AB=AC, ∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一)
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一)
∵AB=AC, AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一)
综上可得:如图,在△ABC中,
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合
思考:
为什么不一样?
例3 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
典例解析
图②
图①
证明:(1)如图①,过A作
AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图①
G
方法总结:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
图②
如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
跟踪训练
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线和底边上的高互相
重合,简称“三线合 一”
分类讨论思想的应用
轴对称图形
等腰三角形的性质
2.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
1.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
3.在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
A
B
C
A
B
C
70°或20°
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
4.如图,在△ABC中,AB = AC,D是BC边上的中点,∠B = 30°,求 ∠BAD 和 ∠ADC的度数.
A
B
C
D
解:∵AB=AC,D是BC边上的中点,
∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°.
∴∠ BAC =180° - 30°-30° = 120°.
∴ = 60°.
5.如图,已知△ABC为等腰三角形,BD、CE分别为底角的平分线,且∠DBC=∠F,求证:EC∥DF.
∴∠DBC=∠ECB.
∵∠DBC=∠F,∴∠ECB=∠F,∴EC∥DF.
证明:∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
又∵BD、CE分别为底角的平分线,
∴
如果命运是块顽石,我就化为大锤,将它砸得粉碎!
——欧拉
