人教版数学八年级上册 13.3.1 等腰三角形(第2课时) 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1 等腰三角形(第2课时) 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 09:01:39 | ||
图片预览



文档简介
(共21张PPT)
第2课时
13.3.1 等腰三角形
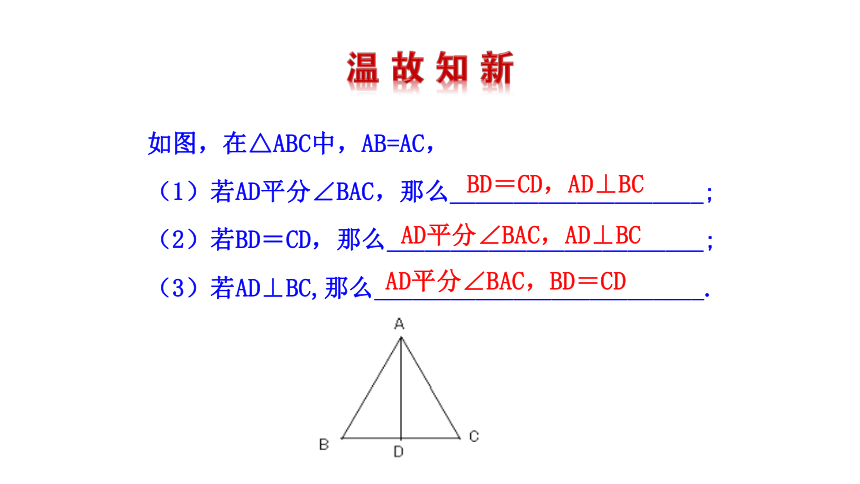
如图,在△ABC中,AB=AC,
(1)若AD平分∠BAC,那么____________________;
(2)若BD=CD,那么_________________________;
(3)若AD⊥BC,那么__________________________.
BD=CD,AD⊥BC
AD平分∠BAC,AD⊥BC
AD平分∠BAC,BD=CD
1.探索等腰三角形的判定定理及其应用.
2.探索等腰三角形的判定定理,进一步体验轴对称的特征,发展空间观念.
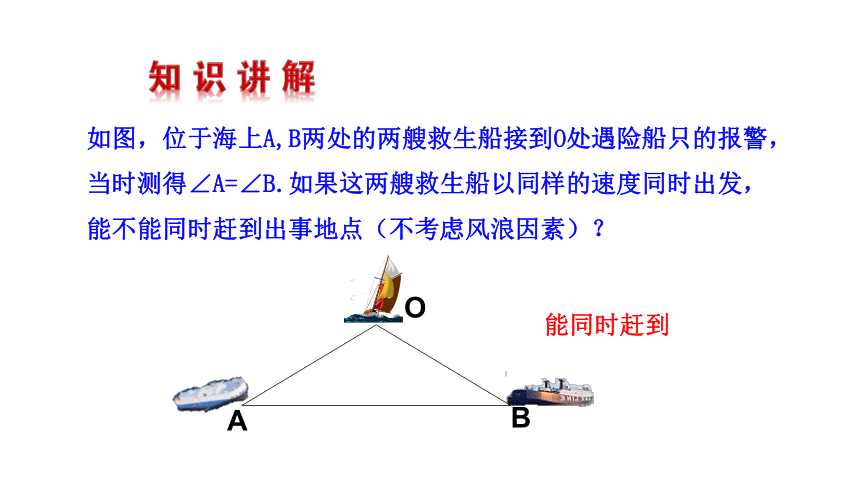
如图,位于海上A,B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
O
B
A
能同时赶到
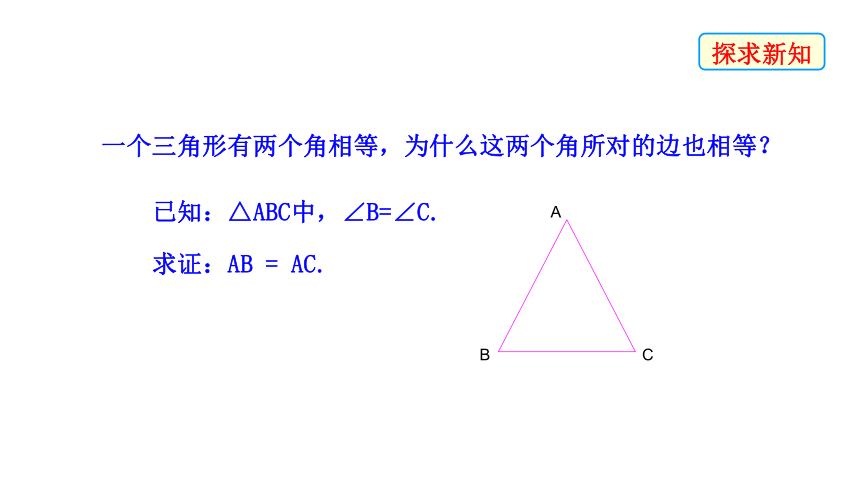
一个三角形有两个角相等,为什么这两个角所对的边也相等?
A
B
C
已知:△ABC中,∠B=∠C.
求证:AB = AC.
探求新知
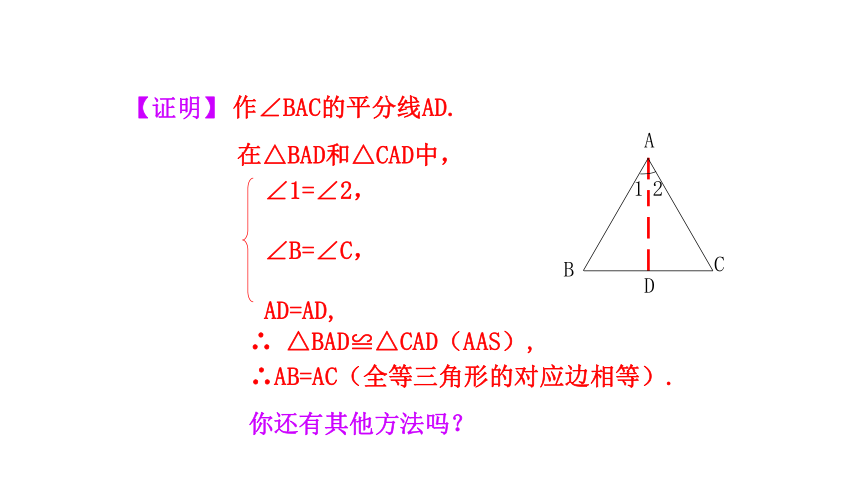
【证明】
作∠BAC的平分线AD.
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C,
AD=AD,
∴ △BAD≌△CAD(AAS),
∴AB=AC(全等三角形的对应边相等).
1
A
B
C
D
2
你还有其他方法吗?
∴ AC=AB. ( )
即△ABC为等腰三角形.
∵∠B=∠C, ( )
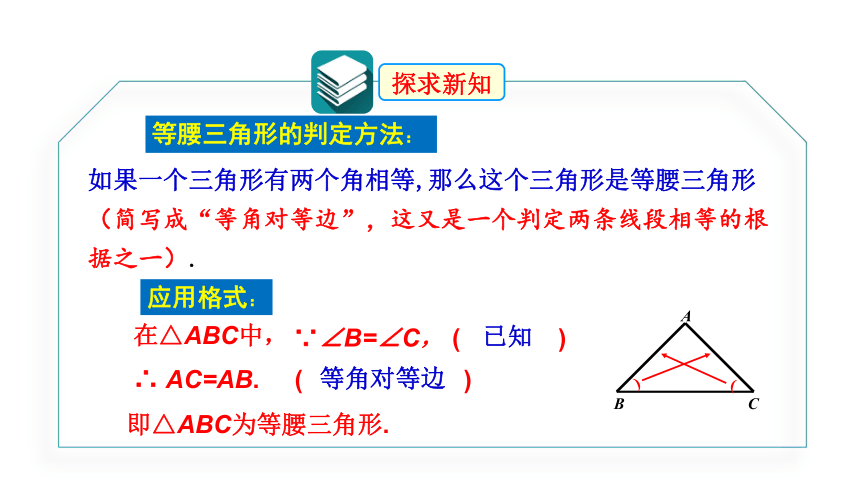
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”,这又是一个判定两条线段相等的根据之一).
已知
等角对等边
在△ABC中,
B
C
A
(
(
应用格式:
探求新知
A
B
C
D
E
例1 已知:如图,∠DAC 是△ABC 的一个外角,AE平分∠DAC,且AE∥BC.
求证:△ABC是等腰三角形.
【证明】∵ AE平分∠DAC,
∴∠DAE = ∠EAC,
∵ AE∥BC,
∴∠DAE=∠B,∠EAC= ∠C,
∴∠B = ∠C,∴AB = AC.
∴△ABC是等腰三角形.
利用等腰三角形的判定定理判定三角形的形状
典例解析
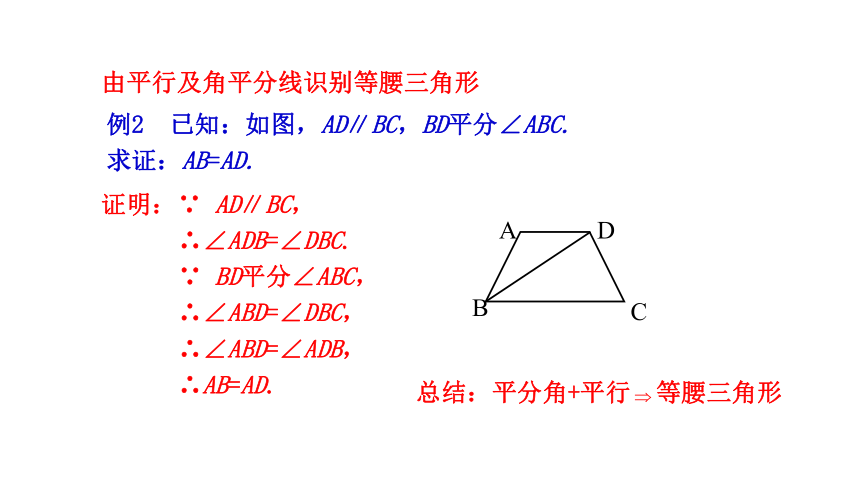
例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
总结:平分角+平行 等腰三角形
由平行及角平分线识别等腰三角形
1.在△ABC中,∠A和∠B的度数如下,能判定 △ABC是等腰三角形的是( )
A. ∠A=50°,∠B=70° B. ∠A=70°,∠B=40°
C. ∠A=30°,∠B=90° D. ∠A=80°,∠B=60°
B
2.如图,已知OC平分∠AOB,CD∥OB,若OD=3cm,则CD等于_______.
3cm
跟踪训练
3.如图,AC 和BD 相交于点O,且AB∥DC,OA =OB.求证:OC =OD.
A
B
C
D
O
【证明】 ∵OA=OB,
∴∠A=∠B,
∵ AB∥CD,
∴∠A=∠C,∠B=∠D(两直线平行,内错角相等),
∴∠C=∠D(等量代换),
∴OC=OD(等角对等边).
例3 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.
通过计算角相等来证明等腰三角形
典例解析
如图所示,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=
∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是 ( )
A.4 B.5 C.6 D.7
C
解析: ∵AB=AC,∠ABC=36°,∴∠BAC=108°,
∴∠BAD=∠DAE=∠EAC=36°,∴等腰三角形有
△ABC,△ABD,△ADE,△ACE,△ACD,△ABE,共有6个.
跟踪训练
例4 已知等腰三角形底边长为a,底边上的高的长为h,求作等腰△ABC.使底边BC=a,底边上的高为h.
a
h
作法:
1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
利用尺规作图作等腰三角形
典例解析
例5 如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
探究EF、BE、FC之间的数量关系.
O
A
B
C
E
F
解:EF=BE+CF.
理由如下:∵ EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO.
∵ BO、CO分别平分∠ABC、∠ACB,
∴∠CBO=∠ABO,∠BCO=∠ACO,
∴∠EOB=∠ABO ,∠FOC=∠ACO,
∴BE=OE,CF=OF,
∴ EF=EO+FO=BE+CF.
A
B
C
O
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?结论还成立吗?
利用等腰三角形的判定证明线段之间的关系
O
A
B
C
M
N
1
2
3
4
5
6
在ΔABC中,OB平分∠ABC, OC平分∠ACB,过O点作MN ∥BC.
ΔAMN的周长=AB+AC吗?为什么?
解:∵ OB平分∠ABC,∴∠1=∠2,
又 ∵MN∥BC,∴∠2=∠3,∴∠1=∠3,
∴OM=BM.
同理得:ON=CN.
∵MN=OM+ON,∴MN=BM+CN.
∵ ΔAMN的周长=AM+MN+AN= AM+BM+CN+AN=AB+AC.
跟踪训练
1.等腰三角形的两种判定方法:①定义,②判定定理.
2.运用等腰三角形的判定定理时,应注意在同一个三角形中.
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍.这个三角形是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
1.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
C
A
3.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
A.1个 B.2个
C.3个 D.4个
D
1
O
a
b
A
4.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.
36°
72°
△ABC、
△DBA、
△BCD
5.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为_____.
9
第5题图
A
B
C
D
第4题图
海到天边天作岸,山登绝顶我为峰
第2课时
13.3.1 等腰三角形
如图,在△ABC中,AB=AC,
(1)若AD平分∠BAC,那么____________________;
(2)若BD=CD,那么_________________________;
(3)若AD⊥BC,那么__________________________.
BD=CD,AD⊥BC
AD平分∠BAC,AD⊥BC
AD平分∠BAC,BD=CD
1.探索等腰三角形的判定定理及其应用.
2.探索等腰三角形的判定定理,进一步体验轴对称的特征,发展空间观念.
如图,位于海上A,B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
O
B
A
能同时赶到
一个三角形有两个角相等,为什么这两个角所对的边也相等?
A
B
C
已知:△ABC中,∠B=∠C.
求证:AB = AC.
探求新知
【证明】
作∠BAC的平分线AD.
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C,
AD=AD,
∴ △BAD≌△CAD(AAS),
∴AB=AC(全等三角形的对应边相等).
1
A
B
C
D
2
你还有其他方法吗?
∴ AC=AB. ( )
即△ABC为等腰三角形.
∵∠B=∠C, ( )
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”,这又是一个判定两条线段相等的根据之一).
已知
等角对等边
在△ABC中,
B
C
A
(
(
应用格式:
探求新知
A
B
C
D
E
例1 已知:如图,∠DAC 是△ABC 的一个外角,AE平分∠DAC,且AE∥BC.
求证:△ABC是等腰三角形.
【证明】∵ AE平分∠DAC,
∴∠DAE = ∠EAC,
∵ AE∥BC,
∴∠DAE=∠B,∠EAC= ∠C,
∴∠B = ∠C,∴AB = AC.
∴△ABC是等腰三角形.
利用等腰三角形的判定定理判定三角形的形状
典例解析
例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
总结:平分角+平行 等腰三角形
由平行及角平分线识别等腰三角形
1.在△ABC中,∠A和∠B的度数如下,能判定 △ABC是等腰三角形的是( )
A. ∠A=50°,∠B=70° B. ∠A=70°,∠B=40°
C. ∠A=30°,∠B=90° D. ∠A=80°,∠B=60°
B
2.如图,已知OC平分∠AOB,CD∥OB,若OD=3cm,则CD等于_______.
3cm
跟踪训练
3.如图,AC 和BD 相交于点O,且AB∥DC,OA =OB.求证:OC =OD.
A
B
C
D
O
【证明】 ∵OA=OB,
∴∠A=∠B,
∵ AB∥CD,
∴∠A=∠C,∠B=∠D(两直线平行,内错角相等),
∴∠C=∠D(等量代换),
∴OC=OD(等角对等边).
例3 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.
通过计算角相等来证明等腰三角形
典例解析
如图所示,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=
∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是 ( )
A.4 B.5 C.6 D.7
C
解析: ∵AB=AC,∠ABC=36°,∴∠BAC=108°,
∴∠BAD=∠DAE=∠EAC=36°,∴等腰三角形有
△ABC,△ABD,△ADE,△ACE,△ACD,△ABE,共有6个.
跟踪训练
例4 已知等腰三角形底边长为a,底边上的高的长为h,求作等腰△ABC.使底边BC=a,底边上的高为h.
a
h
作法:
1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
利用尺规作图作等腰三角形
典例解析
例5 如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
探究EF、BE、FC之间的数量关系.
O
A
B
C
E
F
解:EF=BE+CF.
理由如下:∵ EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO.
∵ BO、CO分别平分∠ABC、∠ACB,
∴∠CBO=∠ABO,∠BCO=∠ACO,
∴∠EOB=∠ABO ,∠FOC=∠ACO,
∴BE=OE,CF=OF,
∴ EF=EO+FO=BE+CF.
A
B
C
O
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?结论还成立吗?
利用等腰三角形的判定证明线段之间的关系
O
A
B
C
M
N
1
2
3
4
5
6
在ΔABC中,OB平分∠ABC, OC平分∠ACB,过O点作MN ∥BC.
ΔAMN的周长=AB+AC吗?为什么?
解:∵ OB平分∠ABC,∴∠1=∠2,
又 ∵MN∥BC,∴∠2=∠3,∴∠1=∠3,
∴OM=BM.
同理得:ON=CN.
∵MN=OM+ON,∴MN=BM+CN.
∵ ΔAMN的周长=AM+MN+AN= AM+BM+CN+AN=AB+AC.
跟踪训练
1.等腰三角形的两种判定方法:①定义,②判定定理.
2.运用等腰三角形的判定定理时,应注意在同一个三角形中.
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍.这个三角形是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
1.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
C
A
3.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
A.1个 B.2个
C.3个 D.4个
D
1
O
a
b
A
4.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.
36°
72°
△ABC、
△DBA、
△BCD
5.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为_____.
9
第5题图
A
B
C
D
第4题图
海到天边天作岸,山登绝顶我为峰
