24.3.1圆周角定理 同步练习(含答案)
文档属性
| 名称 | 24.3.1圆周角定理 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.3.1圆周角定理
一、单选题
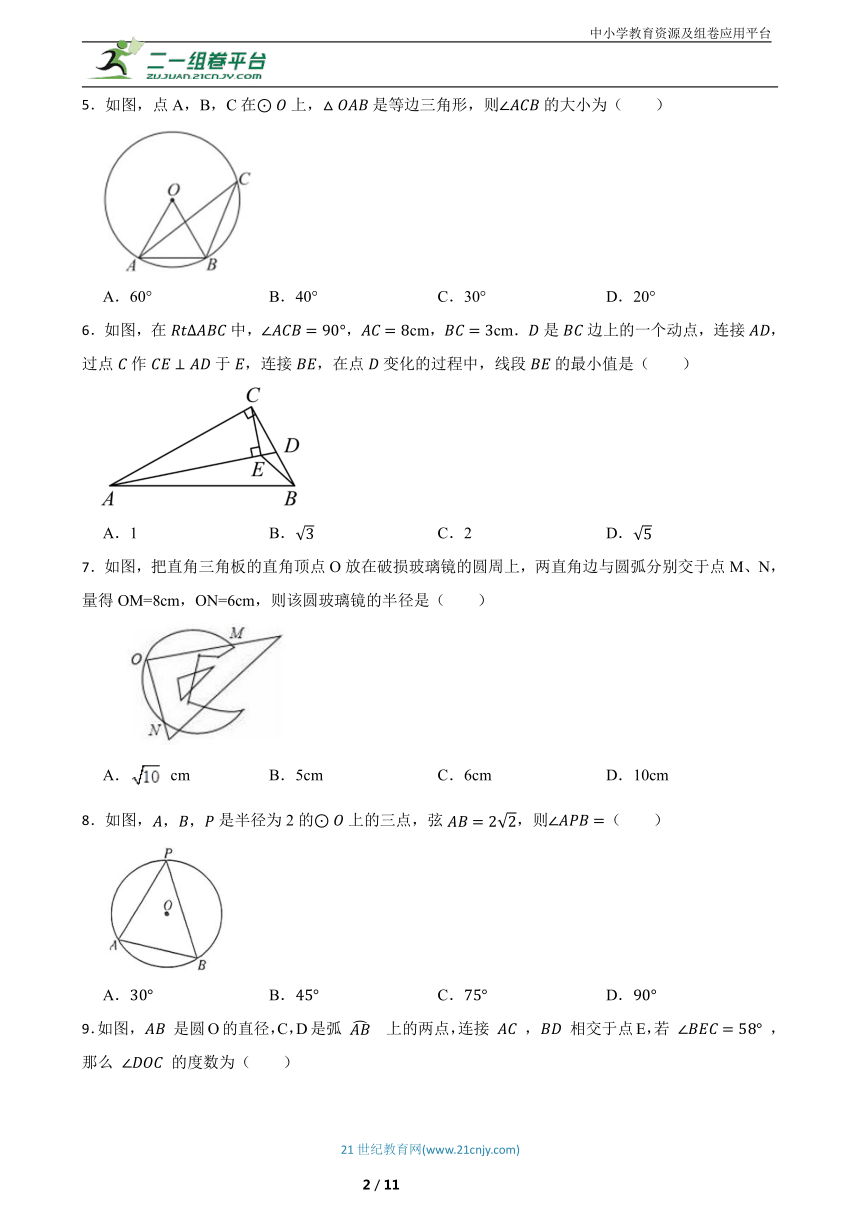
1.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
A.140° B.70° C.60° D.40°
2.如图,是的外接圆,,若的半径的长为1,则( )
A.4 B. C.2 D.
3.如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,BD,OD,OC,若∠ABD=15°,且AD∥OC,则∠BOC的度数为( )
A.120° B.105° C.100° D.110°
4.如图,是的直径,,是上位于两侧的点,若,则度数为( )
A. B. C. D.
5.如图,点A,B,C在上,是等边三角形,则的大小为( )
A.60° B.40° C.30° D.20°
6.如图,在中,,cm,cm.是边上的一个动点,连接,过点作于,连接,在点变化的过程中,线段的最小值是( )
A.1 B. C.2 D.
7.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是( )
A. cm B.5cm C.6cm D.10cm
8.如图,是半径为2的上的三点,弦,则( )
A. B. C. D.
9.如图, 是圆O的直径,C,D是弧 上的两点,连接 , 相交于点E,若 ,那么 的度数为( )
A. B. C. D.
10.如图,在中,,,,P是上的一点,于点H,以为直径作,当与的交点落在上时,的值为( )
A.3 B.4 C.5 D.6
二、填空题
11.如图,已知△ABC的顶点在⊙O上,连接AO,若∠B=60°,则∠OAC= °.
12.如图,四边形内接于⊙,延长交⊙于点E,连接.若,,则 .
13.如图,是上的三个点,,则度数是 .
14.如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB= ,BD=2,则线段AE的长为 .
15.如图,点A是半圆上的三等分点,B是弧的中点,P是直径上一动点.的半径为2,写出的最小值 .
16.如图,分别经过点和点的动直线,交于点C,在线段上取点D,连接.若,且,则当的值最大时,点C的坐标为 .
三、计算题
17.如图,已知、是的两条直径,若,求的度数.
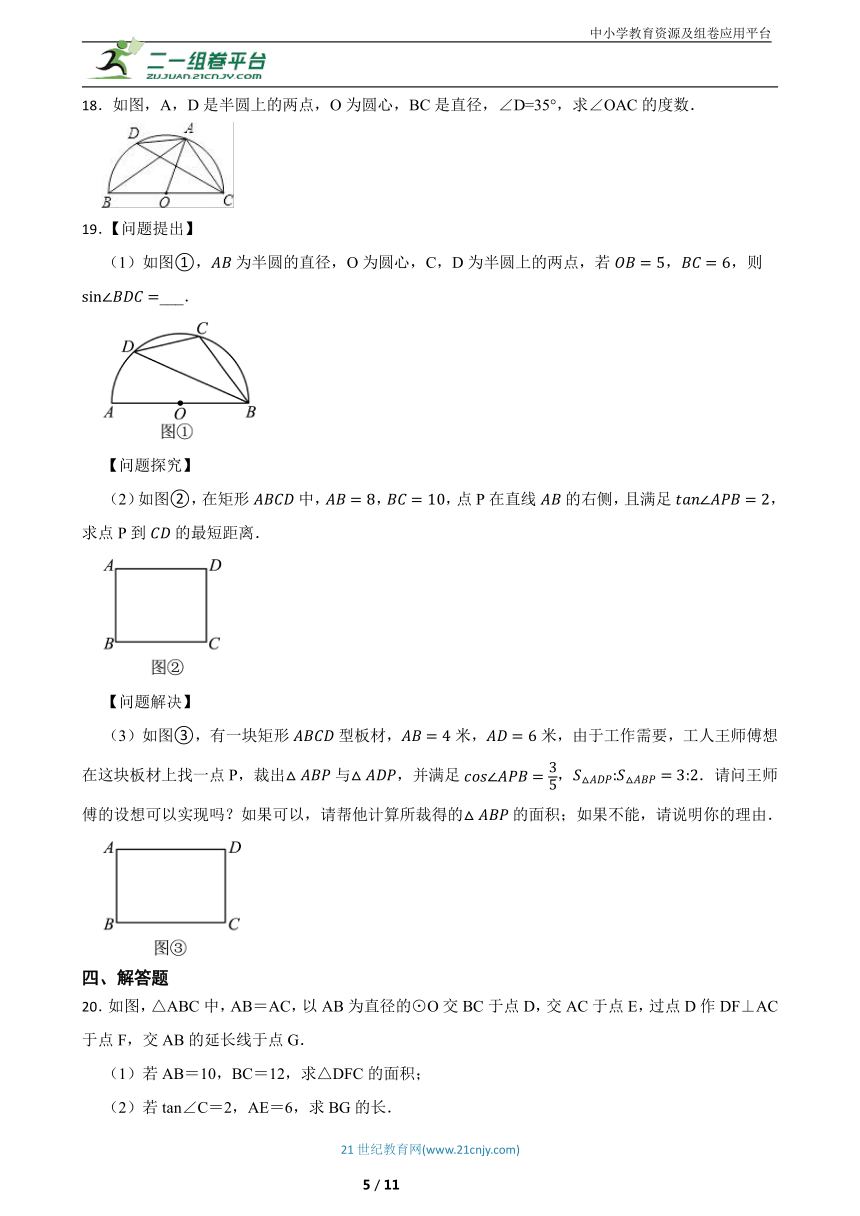
18.如图,A,D是半圆上的两点,O为圆心,BC是直径,∠D=35°,求∠OAC的度数.
19.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
四、解答题
20.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)若AB=10,BC=12,求△DFC的面积;
(2)若tan∠C=2,AE=6,求BG的长.
21.已知的直径为10,点A,点B,点C在上,的平分线交于点D.
(1)求的度数;
(2)若,求的长.
22.如图,已知内接于,是该圆直径,D是弧上的点,线段与交于点E,若,,,.
(1)试用含m的代数式表示k.
(2)若,求k的值.
23.如图,AB为的直径,为圆上的一点(异于点A,BD为的中点,AD,BC相交于点,过点作于点,交BC于点.
(1)证明:.
(2)猜想BC与2DE有怎样的数量关系,并证明你发现的结论.
(3)如图2,连结AC,BD,若,求的值.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】D
【知识点】垂径定理;圆周角定理;解直角三角形
3.【答案】B
【知识点】平行线的性质;三角形内角和定理;圆周角定理
4.【答案】B
【知识点】圆周角定理
5.【答案】C
【知识点】圆周角定理
6.【答案】A
【知识点】三角形三边关系;勾股定理;圆周角定理
7.【答案】B
【知识点】勾股定理;圆周角定理
8.【答案】B
【知识点】勾股定理;圆周角定理
9.【答案】B
【知识点】圆周角定理
10.【答案】C
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质
11.【答案】30
【知识点】等腰三角形的判定与性质;圆周角定理
12.【答案】
【知识点】圆周角定理
13.【答案】
【知识点】圆周角定理
14.【答案】
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质
15.【答案】
【知识点】两点之间线段最短;垂径定理;圆周角定理;轴对称的性质
16.【答案】或
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质;解直角三角形
17.【答案】
【知识点】等腰三角形的性质;圆周角定理
18.【答案】解法一:
解:∵∠D=35°,
∴∠B=∠D=35°,
∵BC是直径,
∴∠BAC=90°.
∴∠ACB=90°﹣∠ABC=55°,
∵OA=OC,
∴∠OAC=∠OCA=55°.
解法二:
解:∵∠D=35°,
∴∠AOC=2∠D=70°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OCA+∠AOC=180°,
∴∠OAC=55°.
【知识点】圆周角定理
19.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
20.【答案】(1)△DFC的面积=8.64;(2)BG=.
【知识点】圆周角定理;相似三角形的判定与性质;解直角三角形
21.【答案】(1)
(2),
【知识点】圆心角、弧、弦的关系;圆周角定理
22.【答案】(1)
(2)
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质;解直角三角形
23.【答案】(1)证明:连结BD,
是的直径,
又为的中点,
∴.
,
.
(2).
证明:延长DE交于点,
,
.
又为的中点,
,
,
,
即.
(3)延长BD,AC交于点.
又为的直径,
设,不妨设,则,
,解得,
又,
,即,
.
【知识点】勾股定理;垂径定理;圆心角、弧、弦的关系;圆周角定理;相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 11
24.3.1圆周角定理
一、单选题
1.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
A.140° B.70° C.60° D.40°
2.如图,是的外接圆,,若的半径的长为1,则( )
A.4 B. C.2 D.
3.如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,BD,OD,OC,若∠ABD=15°,且AD∥OC,则∠BOC的度数为( )
A.120° B.105° C.100° D.110°
4.如图,是的直径,,是上位于两侧的点,若,则度数为( )
A. B. C. D.
5.如图,点A,B,C在上,是等边三角形,则的大小为( )
A.60° B.40° C.30° D.20°
6.如图,在中,,cm,cm.是边上的一个动点,连接,过点作于,连接,在点变化的过程中,线段的最小值是( )
A.1 B. C.2 D.
7.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是( )
A. cm B.5cm C.6cm D.10cm
8.如图,是半径为2的上的三点,弦,则( )
A. B. C. D.
9.如图, 是圆O的直径,C,D是弧 上的两点,连接 , 相交于点E,若 ,那么 的度数为( )
A. B. C. D.
10.如图,在中,,,,P是上的一点,于点H,以为直径作,当与的交点落在上时,的值为( )
A.3 B.4 C.5 D.6
二、填空题
11.如图,已知△ABC的顶点在⊙O上,连接AO,若∠B=60°,则∠OAC= °.
12.如图,四边形内接于⊙,延长交⊙于点E,连接.若,,则 .
13.如图,是上的三个点,,则度数是 .
14.如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB= ,BD=2,则线段AE的长为 .
15.如图,点A是半圆上的三等分点,B是弧的中点,P是直径上一动点.的半径为2,写出的最小值 .
16.如图,分别经过点和点的动直线,交于点C,在线段上取点D,连接.若,且,则当的值最大时,点C的坐标为 .
三、计算题
17.如图,已知、是的两条直径,若,求的度数.
18.如图,A,D是半圆上的两点,O为圆心,BC是直径,∠D=35°,求∠OAC的度数.
19.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
四、解答题
20.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)若AB=10,BC=12,求△DFC的面积;
(2)若tan∠C=2,AE=6,求BG的长.
21.已知的直径为10,点A,点B,点C在上,的平分线交于点D.
(1)求的度数;
(2)若,求的长.
22.如图,已知内接于,是该圆直径,D是弧上的点,线段与交于点E,若,,,.
(1)试用含m的代数式表示k.
(2)若,求k的值.
23.如图,AB为的直径,为圆上的一点(异于点A,BD为的中点,AD,BC相交于点,过点作于点,交BC于点.
(1)证明:.
(2)猜想BC与2DE有怎样的数量关系,并证明你发现的结论.
(3)如图2,连结AC,BD,若,求的值.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】D
【知识点】垂径定理;圆周角定理;解直角三角形
3.【答案】B
【知识点】平行线的性质;三角形内角和定理;圆周角定理
4.【答案】B
【知识点】圆周角定理
5.【答案】C
【知识点】圆周角定理
6.【答案】A
【知识点】三角形三边关系;勾股定理;圆周角定理
7.【答案】B
【知识点】勾股定理;圆周角定理
8.【答案】B
【知识点】勾股定理;圆周角定理
9.【答案】B
【知识点】圆周角定理
10.【答案】C
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质
11.【答案】30
【知识点】等腰三角形的判定与性质;圆周角定理
12.【答案】
【知识点】圆周角定理
13.【答案】
【知识点】圆周角定理
14.【答案】
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质
15.【答案】
【知识点】两点之间线段最短;垂径定理;圆周角定理;轴对称的性质
16.【答案】或
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质;解直角三角形
17.【答案】
【知识点】等腰三角形的性质;圆周角定理
18.【答案】解法一:
解:∵∠D=35°,
∴∠B=∠D=35°,
∵BC是直径,
∴∠BAC=90°.
∴∠ACB=90°﹣∠ABC=55°,
∵OA=OC,
∴∠OAC=∠OCA=55°.
解法二:
解:∵∠D=35°,
∴∠AOC=2∠D=70°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OCA+∠AOC=180°,
∴∠OAC=55°.
【知识点】圆周角定理
19.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
20.【答案】(1)△DFC的面积=8.64;(2)BG=.
【知识点】圆周角定理;相似三角形的判定与性质;解直角三角形
21.【答案】(1)
(2),
【知识点】圆心角、弧、弦的关系;圆周角定理
22.【答案】(1)
(2)
【知识点】勾股定理;圆周角定理;相似三角形的判定与性质;解直角三角形
23.【答案】(1)证明:连结BD,
是的直径,
又为的中点,
∴.
,
.
(2).
证明:延长DE交于点,
,
.
又为的中点,
,
,
,
即.
(3)延长BD,AC交于点.
又为的直径,
设,不妨设,则,
,解得,
又,
,即,
.
【知识点】勾股定理;垂径定理;圆心角、弧、弦的关系;圆周角定理;相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 11
