24.3.2圆内接四边形 同步练习(含答案)
文档属性
| 名称 | 24.3.2圆内接四边形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 296.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.3.2圆内接四边形
一、填空题
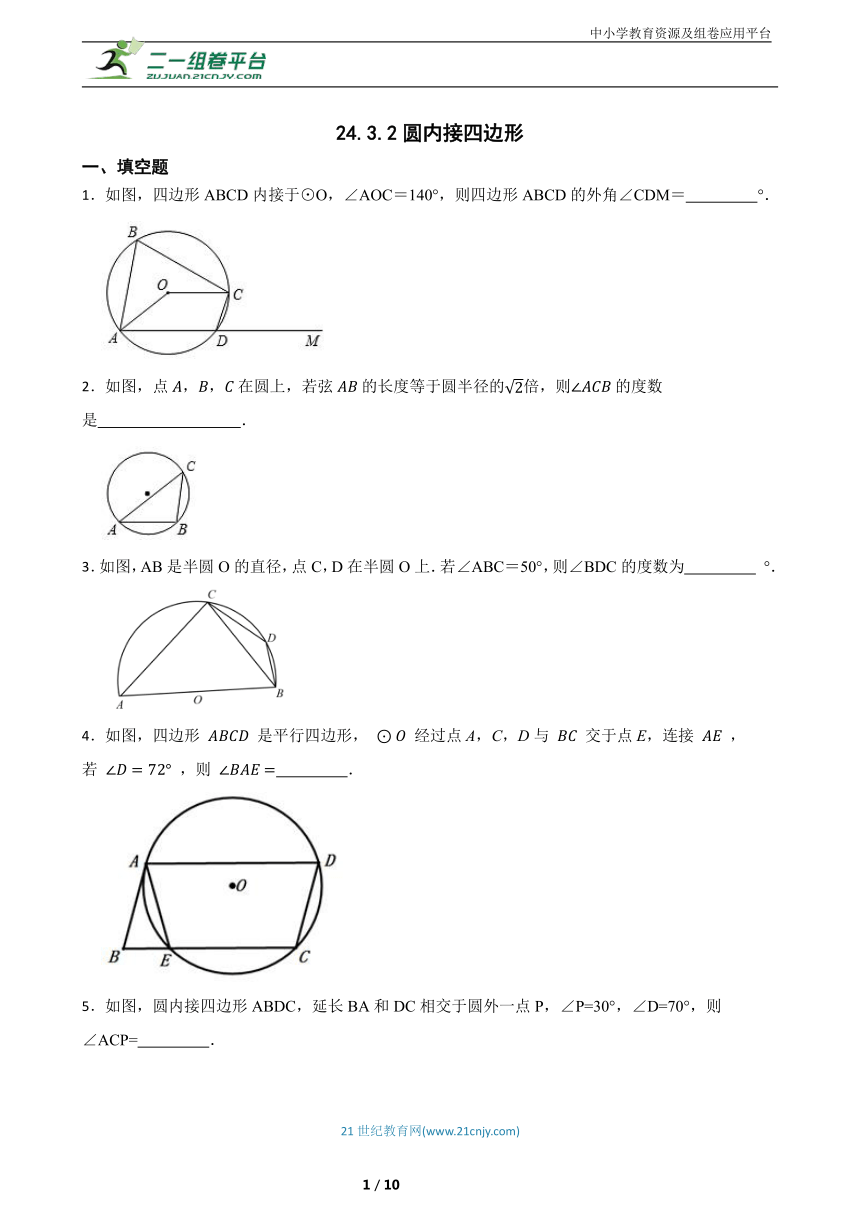
1.如图,四边形ABCD内接于⊙O,∠AOC=140°,则四边形ABCD的外角∠CDM= °.
2.如图,点,,在圆上,若弦的长度等于圆半径的倍,则的度数是 .
3.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为 °.
4.如图,四边形 是平行四边形, 经过点A,C,D与 交于点E,连接 ,若 ,则 .
5.如图,圆内接四边形ABDC,延长BA和DC相交于圆外一点P,∠P=30°,∠D=70°,则∠ACP= .
6.如图,在等边三角形ABC中,点D,E分别是边BC,CA上的点,且BD=CE,连结AD,BE交于点P.连接CP,若CP⊥AP时,则AE:CE= ;设△ABC的面积为S1,四边形CDPE的面积为S2,则= .
二、单选题
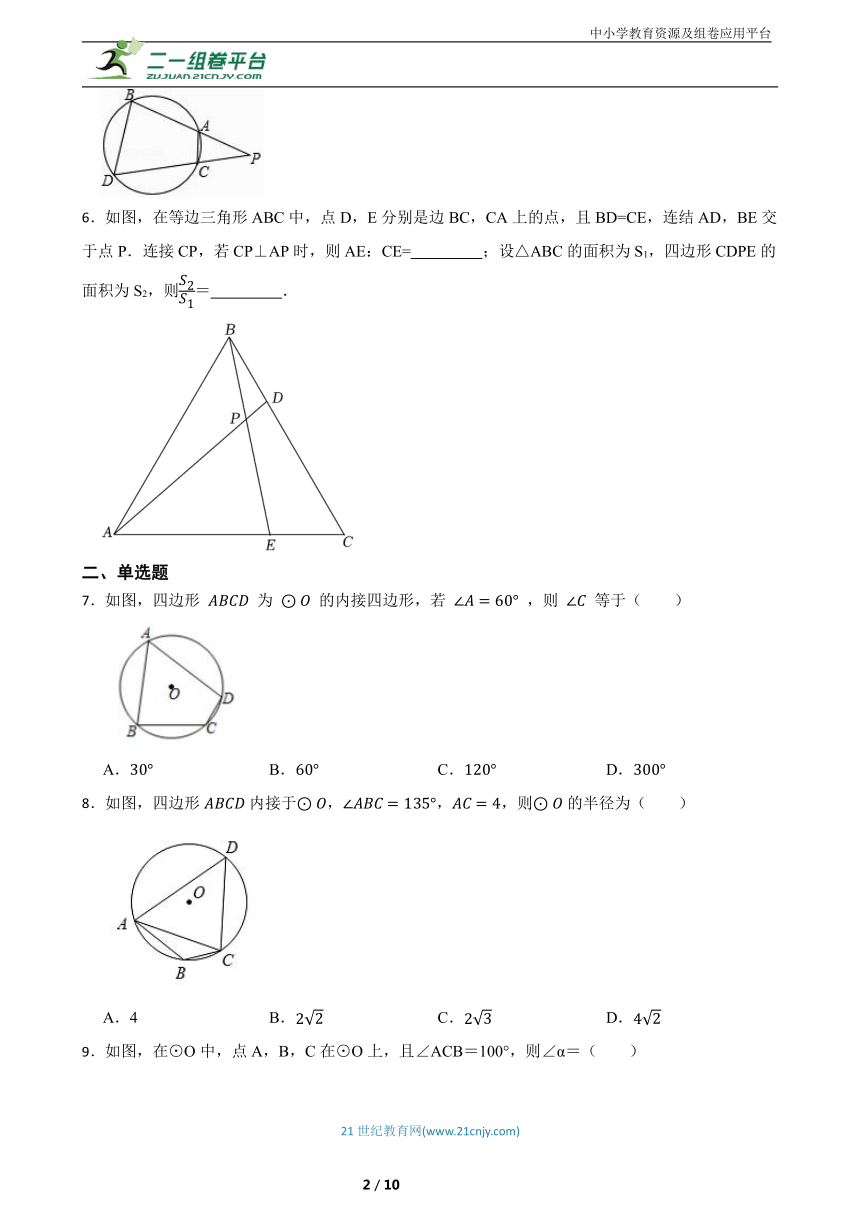
7.如图,四边形 为 的内接四边形,若 ,则 等于( )
A. B. C. D.
8.如图,四边形内接于,,,则的半径为( )
A.4 B. C. D.
9.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=100°,则∠α=( )
A.80° B.100° C.120° D.160°
10.如图,四边形内接于,在延长线上,若,则的度数是( )
A. B. C. D.
11.如图,点A,B,C均在⊙上,当时,的度数是( )
A.100° B.110° C.120° D.130°
12.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BMO=120°,则⊙C的半径长为( )
A.6 B.5 C.3 D.
13.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
A.130° B.100° C.65° D.50°
14.若四边形ABCD是⊙O的内接四边形,且∠A:∠B:∠C=1:3:8,则∠D的度数是( )
A.10° B.30° C.80° D.120°
15.如图, 是半圆O的直径,点C,D在半圆O上.若 ,则 的度数为( )
A. B. C. D.
16.如图, 已知中, 直径于点H, 点D在上, 且,过点A作于点E, 已知的周长为, 且, 则的半径长为( )
A. B. C. D.
三、解答题
17.(1)如图1,是的直径,C、D是上的两点,若,,求
①的度数
②的度数
(2)如图2,的弦垂直平分半径,若的半径为4,求弦的长.
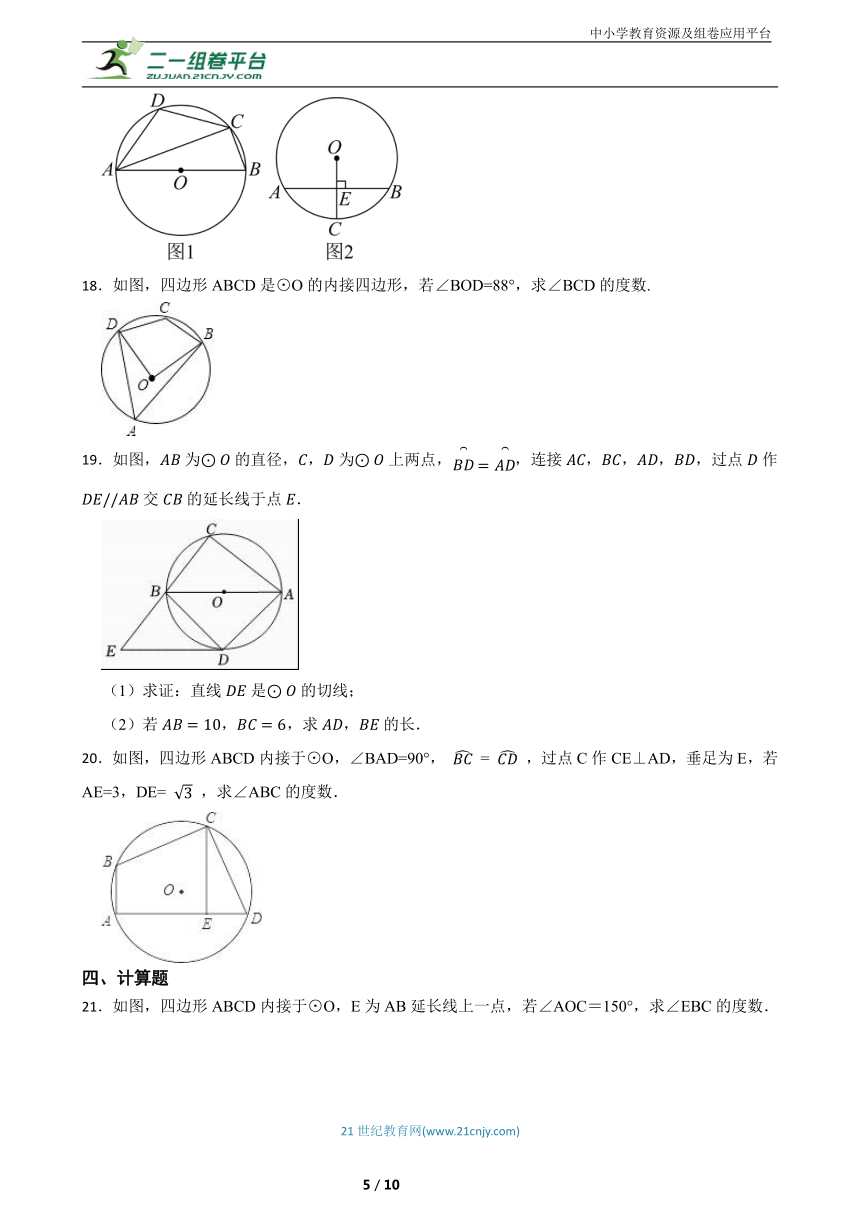
18.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,求∠BCD的度数.
19.如图,为的直径,,为上两点,,连接,,,,过点作交的延长线于点.
(1)求证:直线是的切线;
(2)若,,求,的长.
20.如图,四边形ABCD内接于⊙O,∠BAD=90°, = ,过点C作CE⊥AD,垂足为E,若AE=3,DE= ,求∠ABC的度数.
四、计算题
21.如图,四边形ABCD内接于⊙O,E为AB延长线上一点,若∠AOC=150°,求∠EBC的度数.
答案解析部分
1.【答案】70.
【知识点】圆内接四边形的性质
2.【答案】或
【知识点】圆周角定理;圆内接四边形的性质
3.【答案】140
【知识点】圆周角定理;圆内接四边形的性质
4.【答案】36°
【知识点】圆内接四边形的性质
5.【答案】80°
【知识点】圆内接四边形的性质
6.【答案】2;
【知识点】三角形全等及其性质;圆内接四边形的性质;相似三角形的判定与性质;直角三角形斜边上的中线
7.【答案】C
【知识点】圆内接四边形的性质
8.【答案】B
【知识点】圆周角定理;圆内接四边形的性质
9.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
10.【答案】A
【知识点】圆内接四边形的性质
11.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
12.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
13.【答案】C
【知识点】圆内接四边形的性质
14.【答案】D
【知识点】圆内接四边形的性质
15.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
16.【答案】D
【知识点】等腰三角形的判定与性质;勾股定理;圆周角定理;圆内接四边形的性质;解直角三角形
17.【答案】(1),;(2)
【知识点】垂径定理;圆周角定理;圆内接四边形的性质
18.【答案】解:∵∠BOD=88°,
∴∠BAD=88°÷2=44°,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠BCD=180°,
∴∠BCD=180°﹣44°=136°.
【知识点】圆周角定理;圆内接四边形的性质
19.【答案】(1)证明:连接,
,
,
,
,
是的半径,
直线是的切线;
(2)解:连接,
为的直径,
,
,,
,
,
,
,
,
,
,
,
四边形是圆内接四边形,
,
,
,
∽,
,
,
,
的长为,的长为.
【知识点】圆心角、弧、弦的关系;圆周角定理;圆内接四边形的性质;相似三角形的应用
20.【答案】解:作BF⊥CE于F,∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,∴∠BCF=∠D.又BC=CD,∴Rt△BCF≌Rt△CDE.∴BF=CE.又∵∠BFE=∠AEF=∠A=90°,∴四边形ABFE是矩形.∴BF=AE.∴AE=CE=3,在Rt△CDE中∵∴∠D=60°∵∠ABC+∠D=180°∴∠ABC=120°.
【知识点】圆内接四边形的性质
21.【答案】
【知识点】圆周角定理;圆内接四边形的性质
21世纪教育网(www.21cnjy.com)
10 / 10
24.3.2圆内接四边形
一、填空题
1.如图,四边形ABCD内接于⊙O,∠AOC=140°,则四边形ABCD的外角∠CDM= °.
2.如图,点,,在圆上,若弦的长度等于圆半径的倍,则的度数是 .
3.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为 °.
4.如图,四边形 是平行四边形, 经过点A,C,D与 交于点E,连接 ,若 ,则 .
5.如图,圆内接四边形ABDC,延长BA和DC相交于圆外一点P,∠P=30°,∠D=70°,则∠ACP= .
6.如图,在等边三角形ABC中,点D,E分别是边BC,CA上的点,且BD=CE,连结AD,BE交于点P.连接CP,若CP⊥AP时,则AE:CE= ;设△ABC的面积为S1,四边形CDPE的面积为S2,则= .
二、单选题
7.如图,四边形 为 的内接四边形,若 ,则 等于( )
A. B. C. D.
8.如图,四边形内接于,,,则的半径为( )
A.4 B. C. D.
9.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=100°,则∠α=( )
A.80° B.100° C.120° D.160°
10.如图,四边形内接于,在延长线上,若,则的度数是( )
A. B. C. D.
11.如图,点A,B,C均在⊙上,当时,的度数是( )
A.100° B.110° C.120° D.130°
12.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BMO=120°,则⊙C的半径长为( )
A.6 B.5 C.3 D.
13.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
A.130° B.100° C.65° D.50°
14.若四边形ABCD是⊙O的内接四边形,且∠A:∠B:∠C=1:3:8,则∠D的度数是( )
A.10° B.30° C.80° D.120°
15.如图, 是半圆O的直径,点C,D在半圆O上.若 ,则 的度数为( )
A. B. C. D.
16.如图, 已知中, 直径于点H, 点D在上, 且,过点A作于点E, 已知的周长为, 且, 则的半径长为( )
A. B. C. D.
三、解答题
17.(1)如图1,是的直径,C、D是上的两点,若,,求
①的度数
②的度数
(2)如图2,的弦垂直平分半径,若的半径为4,求弦的长.
18.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,求∠BCD的度数.
19.如图,为的直径,,为上两点,,连接,,,,过点作交的延长线于点.
(1)求证:直线是的切线;
(2)若,,求,的长.
20.如图,四边形ABCD内接于⊙O,∠BAD=90°, = ,过点C作CE⊥AD,垂足为E,若AE=3,DE= ,求∠ABC的度数.
四、计算题
21.如图,四边形ABCD内接于⊙O,E为AB延长线上一点,若∠AOC=150°,求∠EBC的度数.
答案解析部分
1.【答案】70.
【知识点】圆内接四边形的性质
2.【答案】或
【知识点】圆周角定理;圆内接四边形的性质
3.【答案】140
【知识点】圆周角定理;圆内接四边形的性质
4.【答案】36°
【知识点】圆内接四边形的性质
5.【答案】80°
【知识点】圆内接四边形的性质
6.【答案】2;
【知识点】三角形全等及其性质;圆内接四边形的性质;相似三角形的判定与性质;直角三角形斜边上的中线
7.【答案】C
【知识点】圆内接四边形的性质
8.【答案】B
【知识点】圆周角定理;圆内接四边形的性质
9.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
10.【答案】A
【知识点】圆内接四边形的性质
11.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
12.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
13.【答案】C
【知识点】圆内接四边形的性质
14.【答案】D
【知识点】圆内接四边形的性质
15.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
16.【答案】D
【知识点】等腰三角形的判定与性质;勾股定理;圆周角定理;圆内接四边形的性质;解直角三角形
17.【答案】(1),;(2)
【知识点】垂径定理;圆周角定理;圆内接四边形的性质
18.【答案】解:∵∠BOD=88°,
∴∠BAD=88°÷2=44°,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠BCD=180°,
∴∠BCD=180°﹣44°=136°.
【知识点】圆周角定理;圆内接四边形的性质
19.【答案】(1)证明:连接,
,
,
,
,
是的半径,
直线是的切线;
(2)解:连接,
为的直径,
,
,,
,
,
,
,
,
,
,
,
四边形是圆内接四边形,
,
,
,
∽,
,
,
,
的长为,的长为.
【知识点】圆心角、弧、弦的关系;圆周角定理;圆内接四边形的性质;相似三角形的应用
20.【答案】解:作BF⊥CE于F,∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,∴∠BCF=∠D.又BC=CD,∴Rt△BCF≌Rt△CDE.∴BF=CE.又∵∠BFE=∠AEF=∠A=90°,∴四边形ABFE是矩形.∴BF=AE.∴AE=CE=3,在Rt△CDE中∵∴∠D=60°∵∠ABC+∠D=180°∴∠ABC=120°.
【知识点】圆内接四边形的性质
21.【答案】
【知识点】圆周角定理;圆内接四边形的性质
21世纪教育网(www.21cnjy.com)
10 / 10
