24.4.2切线的判定与性质 同步练习(含答案)
文档属性
| 名称 | 24.4.2切线的判定与性质 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.4.2切线的判定与性质
阅卷人 一、填空题
得分
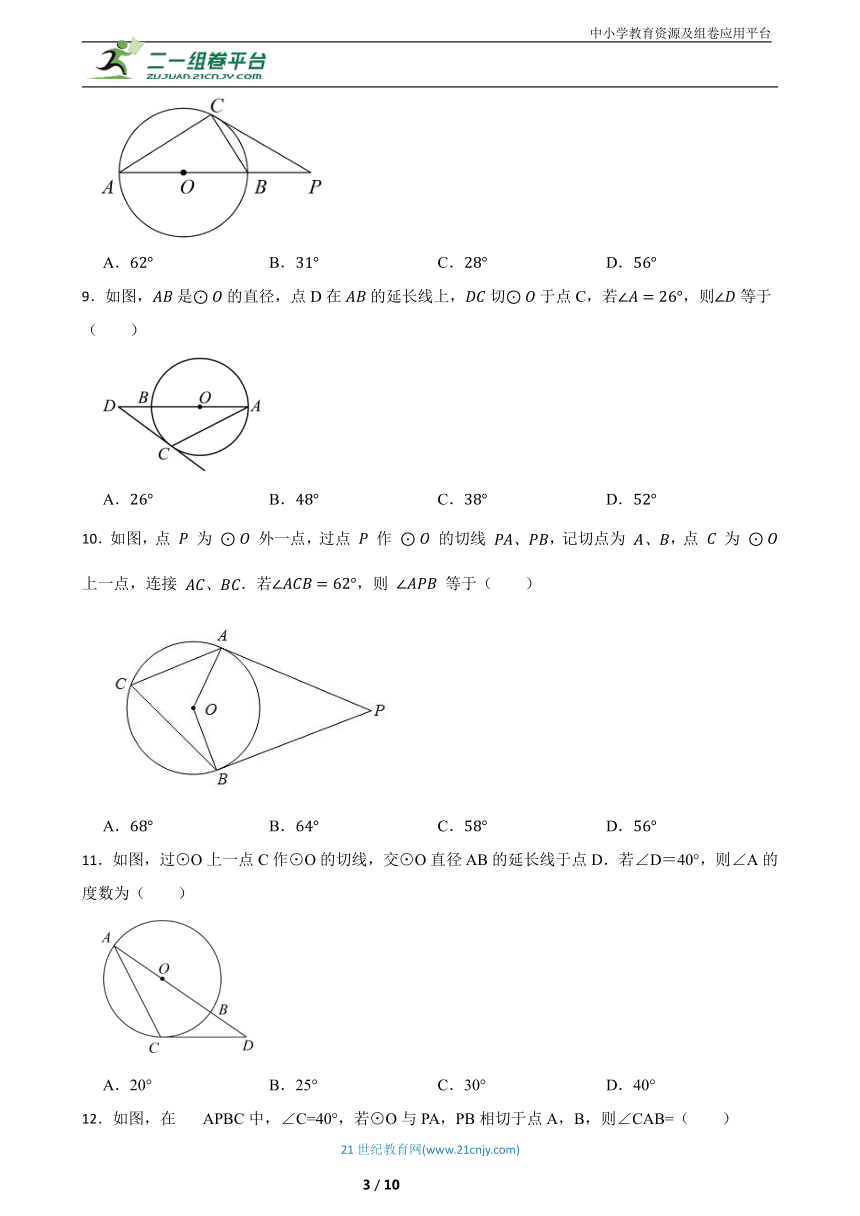
1.如图,在平面直角坐标系中,点A、B均在函数y= (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点A的坐标为(3,2),且⊙A的半径是⊙B的半径的2倍,则点B的坐标为 .
2.如图,点在上,则当 度时,直线PA与相切.
3.如图,是半圆的直径,P是延长线上一点,切半圆于点C,若,则 .
4.如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上,如果∠ACB=70°,那么∠P的度数是 .
5.如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
6.如图,AB是半圆O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC, ,AD=3.给出下列结论:
①AC平分∠BAD;②△ABC∽△ACE;③AB=3PB;④S△ABC=5,
②根据两角相等两三角形相似即可判断;
③由AB是⊙O的直径,PE是切线,可证得∠PCB=∠PAC,即可证得△PCB∽△PAC,然后由相似三角形的对应边成比例与PB:PC=1:2,即可求得答案;
④首先过点O作OH⊥AD于点H,则AH= AD= ,四边形OCEH是矩形,即可得AE= +OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案;
其中正确的是 (写出所有正确结论的序号).
阅卷人 二、单选题
得分
7.下列命题正确是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有两条边对应相等的两个直角三角形全等
C.垂直于圆的半径的直线是切线
D.对角线相等的平行四边形是矩形
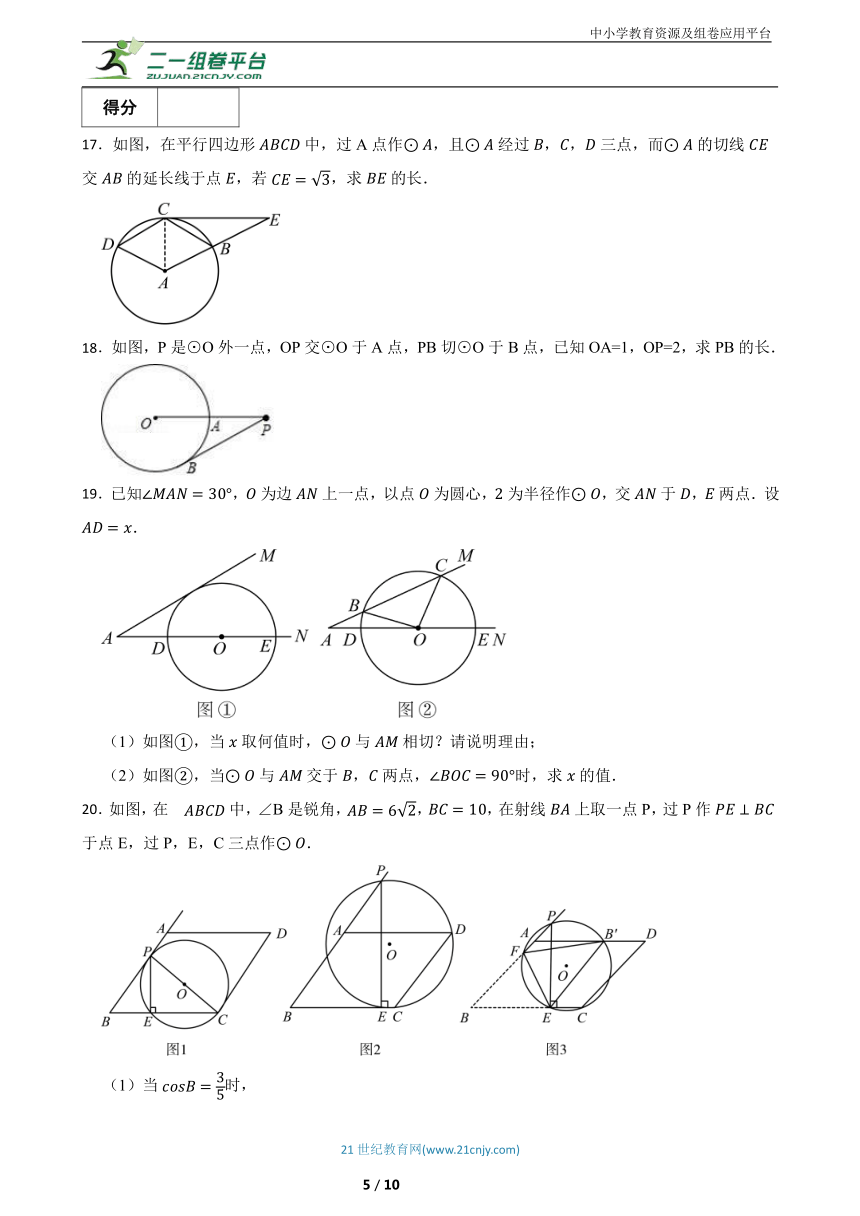
8.如图,内接于圆,,过点的切线交的延长线于点.则( )
A. B. C. D.
9.如图,是的直径,点D在的延长线上,切于点C,若,则等于( )
A. B. C. D.
10.如图,点 为 外一点,过点 作 的切线 ,记切点为 ,点 为 上一点,连接 .若,则 等于( )
A. B. C. D.
11.如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
A.20° B.25° C.30° D.40°
12.如图,在 APBC中,∠C=40°,若⊙O与PA,PB相切于点A,B,则∠CAB=( )
A.40° B.50° C.60° D.70°
13.如图,三角板、量角器和直尺如图摆放,三角板的斜边与半圆相切于点,点B、D、E分别与直尺的刻度1、9、重合,则三角板直角边的长为( )
[ERRORIMAGE:http://tikupic.21cnjy.com/ct20241o/d4/8d/d48de97e4b41f07f613ff5a2b8a82c8b.png]
A. B. C.5 D.6
14.如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA PB;②PC OC=OP CD;③OA2=OD OP;④OA(CP﹣CD)=AP CD,正确的结论有( )个.
A.1 B.2 C.3 D.4
15.如图,点在外,连接,作的垂直平分线交于点;以点为圆心,长为半径作,交于点,,作直线,,直线交的延长线于点.若,,有下列两个结论:①是的切线;②的半径长为3.对于这两个结论,说法正确的是( )
[ERRORIMAGE:http://tikupic.21cnjy.com/ct20241o/4a/ca/4aca73ad8b928a8400ea5255a130a866.png]
A.①对②不对 B.①不对②对 C.①②均对 D.①②均不对
16.如图已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点, DC是⊙O的切线,C是切点,连结AC,若∠CAB=30°,则BD的长为( )
A.R B.R C.2R D.R
阅卷人 三、解答题
得分
17.如图,在平行四边形中,过A点作,且经过,,三点,而的切线交的延长线于点,若,求的长.
18.如图,P是⊙O外一点,OP交⊙O于A点,PB切⊙O于B点,已知OA=1,OP=2,求PB的长.
19.已知,为边上一点,以点为圆心,为半径作,交于,两点.设.
(1)如图,当取何值时,与相切?请说明理由;
(2)如图,当与交于,两点,时,求的值.
20.如图,在中,∠B是锐角,,,在射线上取一点P,过P作于点E,过P,E,C三点作.
(1)当时,
①如图1,若与相切于点P,连结,求的长;
②如图2,若经过点D,求的半径长.
(2)如图3,已知与射线交于另一点F,将沿所在的直线翻折,点B的对应点记为,且恰好同时落在和边上,求此时的长.
阅卷人 四、计算题
得分
21.如图,已知内接于,为直径,延长至D,过D作切线,切点为E,且,连接.,,求的半径.
22.如图1,一个圆球放置在V型架中.图2是它的平面示意图,CA、CB都是⊙O的切线,切点分别是A、B,如果⊙O的半径为cm,且AB=6cm,求∠ACB.
23.筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点、,筒车的轴心距离水面的高度长为,筒车上均匀分布着若干个盛水筒.若以某个盛水筒刚浮出水面时开始计算时间.
(1)经过多长时间,盛水筒首次到达最高点?
(2)浮出水面3.4秒后,盛水筒距离水面多高?
(3)若接水槽所在直线是的切线,且与直线交于点,.求盛水筒从最高点开始,至少经过多长时间恰好在直线上.(参考数据:,,)
答案解析部分
1.【答案】(1,6)
【知识点】切线的性质;反比例函数图象上点的坐标特征
2.【答案】90
【知识点】切线的判定
3.【答案】
【知识点】圆周角定理;切线的性质
4.【答案】40°
【知识点】多边形内角与外角;圆周角定理;切线的性质
5.【答案】 或
【知识点】切线的性质;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
6.【答案】①②③④
【知识点】圆周角定理;切线的性质;相似三角形的判定与性质
7.【答案】D
【知识点】直角三角形全等的判定-HL;平行四边形的判定;矩形的判定;切线的判定
8.【答案】B
【知识点】三角形的外角性质;切线的性质
9.【答案】C
【知识点】圆周角定理;切线的性质
10.【答案】D
【知识点】圆周角定理;切线的性质
11.【答案】B
【知识点】切线的性质
12.【答案】D
【知识点】菱形的判定与性质;切线的性质
13.【答案】D
【知识点】含30°角的直角三角形;勾股定理;切线的性质
14.【答案】D
【知识点】切线的性质;相似三角形的判定与性质
15.【答案】A
【知识点】圆周角定理;切线的判定;相似三角形的判定与性质
16.【答案】A
【知识点】切线的性质
17.【答案】1
【知识点】含30°角的直角三角形;勾股定理;切线的性质
18.【答案】解:连接OB,
∵PB切⊙O于点B,
∴∠B=90°,
∵OA=1,
∴OB=OA=R=1,
∴OP=2,
∴PB= .
【知识点】勾股定理;切线的性质
19.【答案】(1)解:如图,过点作于点,当时,
∵与相切,,
∴,
∴;
(2)解:如图,过点作于点,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
【知识点】等腰三角形的判定;含30°角的直角三角形;垂径定理;切线的性质
20.【答案】(1)①;②的半径长为;
(2).
【知识点】勾股定理;圆周角定理;切线的性质;解直角三角形
21.【答案】半径
【知识点】勾股定理;矩形的判定;切线的性质
22.【答案】解:如图,连接OC交AB于点D∵CA、CB分别是⊙O的切线∴CA=CB,OC平分∠ACB∴OC⊥AB∵AB=6∴BD=3在Rt△OBD中∵OB=∴sin∠BOD=∴∠BOD=60°∵B是切点∴OB⊥BC∴∠OCB=30°∴∠ACB=60°.
【知识点】切线的性质;解直角三角形
23.【答案】(1)27.4秒;(2)0.7m;(3)7.6秒
【知识点】切线的性质;求特殊角的三角函数值;解直角三角形
21世纪教育网(www.21cnjy.com)
2 / 10
24.4.2切线的判定与性质
阅卷人 一、填空题
得分
1.如图,在平面直角坐标系中,点A、B均在函数y= (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点A的坐标为(3,2),且⊙A的半径是⊙B的半径的2倍,则点B的坐标为 .
2.如图,点在上,则当 度时,直线PA与相切.
3.如图,是半圆的直径,P是延长线上一点,切半圆于点C,若,则 .
4.如图,PA、PB是⊙O的切线,切点分别为A、B两点,点C在⊙O上,如果∠ACB=70°,那么∠P的度数是 .
5.如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
6.如图,AB是半圆O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC, ,AD=3.给出下列结论:
①AC平分∠BAD;②△ABC∽△ACE;③AB=3PB;④S△ABC=5,
②根据两角相等两三角形相似即可判断;
③由AB是⊙O的直径,PE是切线,可证得∠PCB=∠PAC,即可证得△PCB∽△PAC,然后由相似三角形的对应边成比例与PB:PC=1:2,即可求得答案;
④首先过点O作OH⊥AD于点H,则AH= AD= ,四边形OCEH是矩形,即可得AE= +OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案;
其中正确的是 (写出所有正确结论的序号).
阅卷人 二、单选题
得分
7.下列命题正确是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有两条边对应相等的两个直角三角形全等
C.垂直于圆的半径的直线是切线
D.对角线相等的平行四边形是矩形
8.如图,内接于圆,,过点的切线交的延长线于点.则( )
A. B. C. D.
9.如图,是的直径,点D在的延长线上,切于点C,若,则等于( )
A. B. C. D.
10.如图,点 为 外一点,过点 作 的切线 ,记切点为 ,点 为 上一点,连接 .若,则 等于( )
A. B. C. D.
11.如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
A.20° B.25° C.30° D.40°
12.如图,在 APBC中,∠C=40°,若⊙O与PA,PB相切于点A,B,则∠CAB=( )
A.40° B.50° C.60° D.70°
13.如图,三角板、量角器和直尺如图摆放,三角板的斜边与半圆相切于点,点B、D、E分别与直尺的刻度1、9、重合,则三角板直角边的长为( )
[ERRORIMAGE:http://tikupic.21cnjy.com/ct20241o/d4/8d/d48de97e4b41f07f613ff5a2b8a82c8b.png]
A. B. C.5 D.6
14.如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA PB;②PC OC=OP CD;③OA2=OD OP;④OA(CP﹣CD)=AP CD,正确的结论有( )个.
A.1 B.2 C.3 D.4
15.如图,点在外,连接,作的垂直平分线交于点;以点为圆心,长为半径作,交于点,,作直线,,直线交的延长线于点.若,,有下列两个结论:①是的切线;②的半径长为3.对于这两个结论,说法正确的是( )
[ERRORIMAGE:http://tikupic.21cnjy.com/ct20241o/4a/ca/4aca73ad8b928a8400ea5255a130a866.png]
A.①对②不对 B.①不对②对 C.①②均对 D.①②均不对
16.如图已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点, DC是⊙O的切线,C是切点,连结AC,若∠CAB=30°,则BD的长为( )
A.R B.R C.2R D.R
阅卷人 三、解答题
得分
17.如图,在平行四边形中,过A点作,且经过,,三点,而的切线交的延长线于点,若,求的长.
18.如图,P是⊙O外一点,OP交⊙O于A点,PB切⊙O于B点,已知OA=1,OP=2,求PB的长.
19.已知,为边上一点,以点为圆心,为半径作,交于,两点.设.
(1)如图,当取何值时,与相切?请说明理由;
(2)如图,当与交于,两点,时,求的值.
20.如图,在中,∠B是锐角,,,在射线上取一点P,过P作于点E,过P,E,C三点作.
(1)当时,
①如图1,若与相切于点P,连结,求的长;
②如图2,若经过点D,求的半径长.
(2)如图3,已知与射线交于另一点F,将沿所在的直线翻折,点B的对应点记为,且恰好同时落在和边上,求此时的长.
阅卷人 四、计算题
得分
21.如图,已知内接于,为直径,延长至D,过D作切线,切点为E,且,连接.,,求的半径.
22.如图1,一个圆球放置在V型架中.图2是它的平面示意图,CA、CB都是⊙O的切线,切点分别是A、B,如果⊙O的半径为cm,且AB=6cm,求∠ACB.
23.筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点、,筒车的轴心距离水面的高度长为,筒车上均匀分布着若干个盛水筒.若以某个盛水筒刚浮出水面时开始计算时间.
(1)经过多长时间,盛水筒首次到达最高点?
(2)浮出水面3.4秒后,盛水筒距离水面多高?
(3)若接水槽所在直线是的切线,且与直线交于点,.求盛水筒从最高点开始,至少经过多长时间恰好在直线上.(参考数据:,,)
答案解析部分
1.【答案】(1,6)
【知识点】切线的性质;反比例函数图象上点的坐标特征
2.【答案】90
【知识点】切线的判定
3.【答案】
【知识点】圆周角定理;切线的性质
4.【答案】40°
【知识点】多边形内角与外角;圆周角定理;切线的性质
5.【答案】 或
【知识点】切线的性质;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
6.【答案】①②③④
【知识点】圆周角定理;切线的性质;相似三角形的判定与性质
7.【答案】D
【知识点】直角三角形全等的判定-HL;平行四边形的判定;矩形的判定;切线的判定
8.【答案】B
【知识点】三角形的外角性质;切线的性质
9.【答案】C
【知识点】圆周角定理;切线的性质
10.【答案】D
【知识点】圆周角定理;切线的性质
11.【答案】B
【知识点】切线的性质
12.【答案】D
【知识点】菱形的判定与性质;切线的性质
13.【答案】D
【知识点】含30°角的直角三角形;勾股定理;切线的性质
14.【答案】D
【知识点】切线的性质;相似三角形的判定与性质
15.【答案】A
【知识点】圆周角定理;切线的判定;相似三角形的判定与性质
16.【答案】A
【知识点】切线的性质
17.【答案】1
【知识点】含30°角的直角三角形;勾股定理;切线的性质
18.【答案】解:连接OB,
∵PB切⊙O于点B,
∴∠B=90°,
∵OA=1,
∴OB=OA=R=1,
∴OP=2,
∴PB= .
【知识点】勾股定理;切线的性质
19.【答案】(1)解:如图,过点作于点,当时,
∵与相切,,
∴,
∴;
(2)解:如图,过点作于点,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
【知识点】等腰三角形的判定;含30°角的直角三角形;垂径定理;切线的性质
20.【答案】(1)①;②的半径长为;
(2).
【知识点】勾股定理;圆周角定理;切线的性质;解直角三角形
21.【答案】半径
【知识点】勾股定理;矩形的判定;切线的性质
22.【答案】解:如图,连接OC交AB于点D∵CA、CB分别是⊙O的切线∴CA=CB,OC平分∠ACB∴OC⊥AB∵AB=6∴BD=3在Rt△OBD中∵OB=∴sin∠BOD=∴∠BOD=60°∵B是切点∴OB⊥BC∴∠OCB=30°∴∠ACB=60°.
【知识点】切线的性质;解直角三角形
23.【答案】(1)27.4秒;(2)0.7m;(3)7.6秒
【知识点】切线的性质;求特殊角的三角函数值;解直角三角形
21世纪教育网(www.21cnjy.com)
2 / 10
