24.4直线与圆的位置关系本节综合题(含答案)
文档属性
| 名称 | 24.4直线与圆的位置关系本节综合题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 19:31:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.4直线与圆的位置关系本节综合题
一、单选题
1.如图,为的直径,是的切线,切点为,连接,若,则的度数为( )
A. B. C. D.
2.如图,AB是的直径,过点A作的切线,连接,与交于点D,E是上一点,连接.若,则的度数为( )
A. B. C. D.
3.已如⊙O的半径等于3,圈心O到直线l的距离为5,那么直线l与⊙O的位置关系是 ( )
A.直线l与⊙O相交 B.直线l与⊙O相离
C.直线l与⊙O相切 D.无法确定
4.在平面直角坐标系中,的半径是2,点在y轴上移动,当与x轴相交时,m的取值范围是( )
A. B.
C.或 D.
5.如图,中,,,,以点为圆心,为半径作,当时,与的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
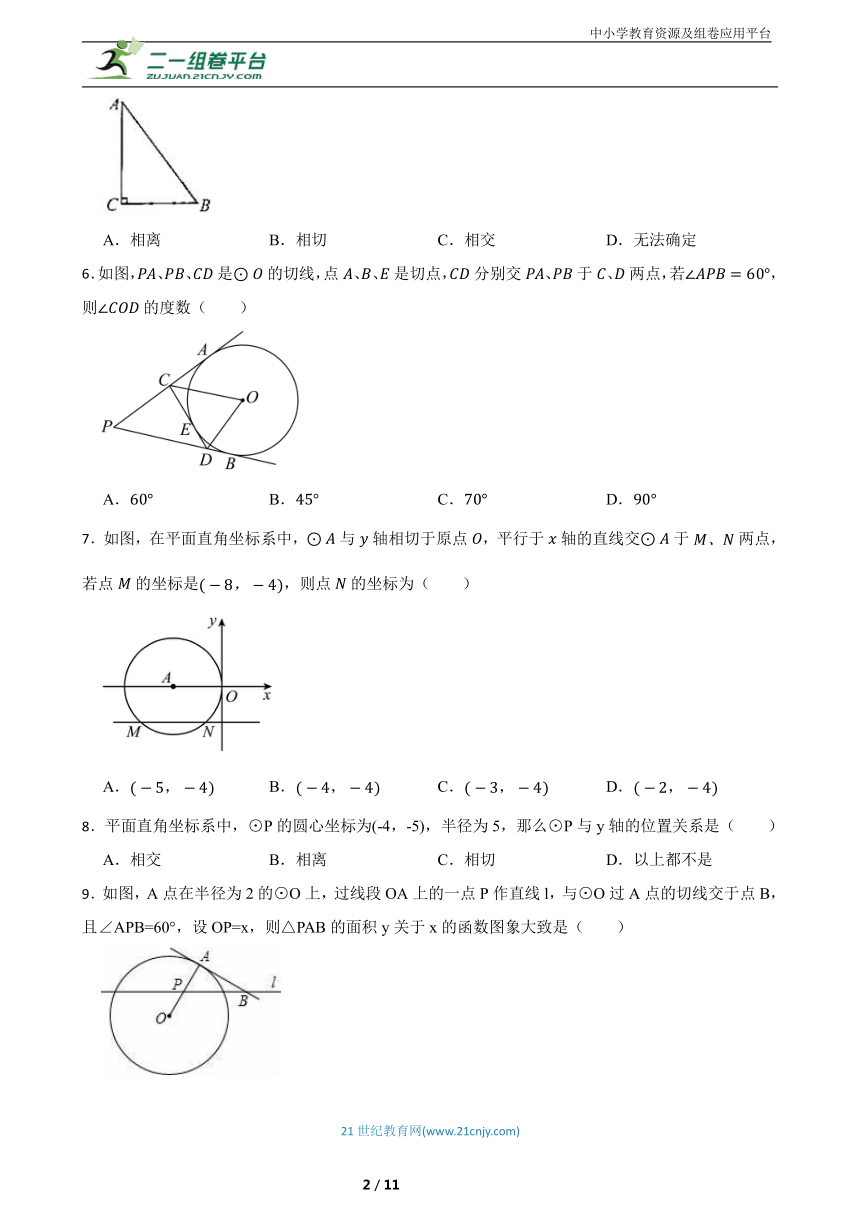
6.如图,、、是的切线,点、、是切点,分别交、于、两点,若,则的度数( )
A. B. C. D.
7.如图,在平面直角坐标系中,与轴相切于原点,平行于轴的直线交于两点,若点的坐标是,则点的坐标为( )
A. B. C. D.
8.平面直角坐标系中,⊙P的圆心坐标为(-4,-5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
9.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
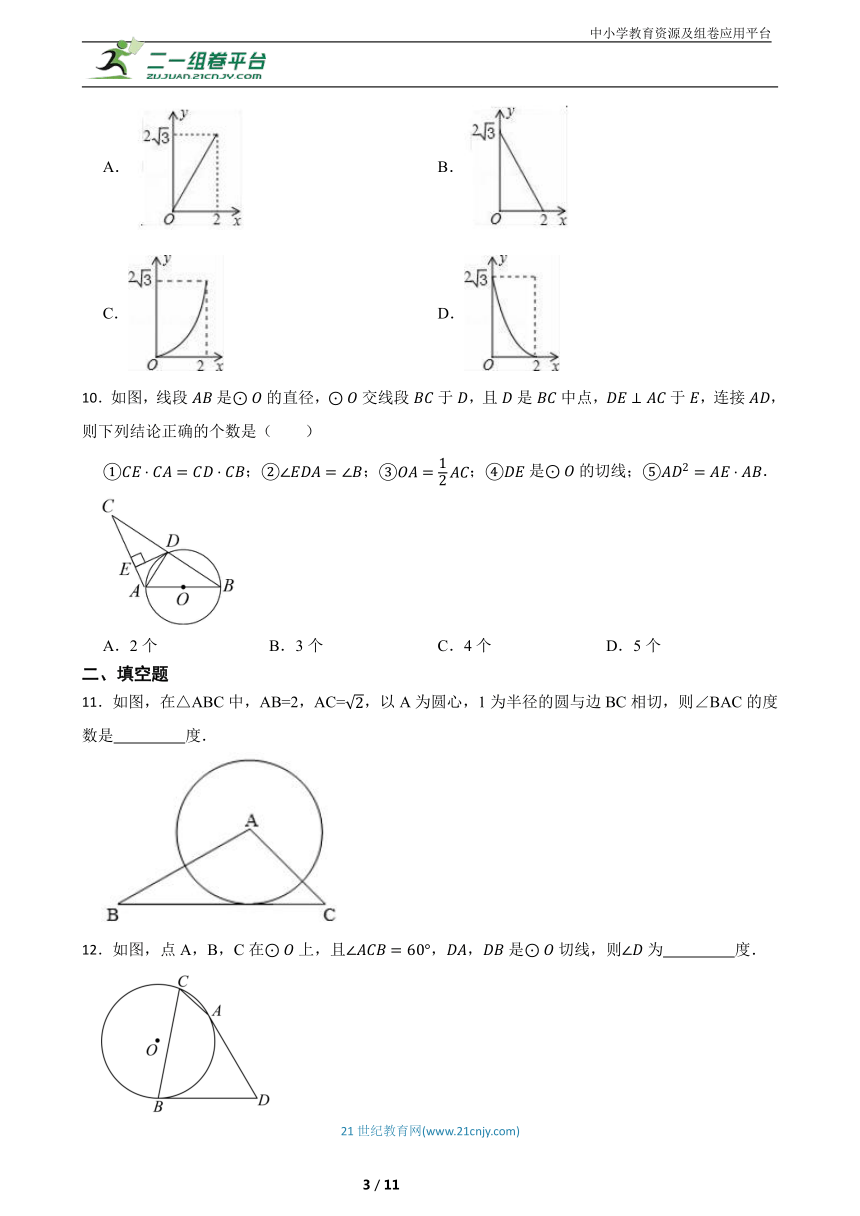
10.如图,线段是的直径,交线段于,且是中点,于,连接,则下列结论正确的个数是( )
;;;是的切线;.
A.2个 B.3个 C.4个 D.5个
二、填空题
11.如图,在△ABC中,AB=2,AC=,以A为圆心,1为半径的圆与边BC相切,则∠BAC的度数是 度.
12.如图,点A,B,C在上,且,,是切线,则为 度.
13.如图,为的切线点A为切点,交于点C,点D在上,连接、、,若,则的度数为 .
14.在 中, , ,以边 的中点 为圆心,作半圆与 相切,点 分别是边 和半圆上的动点,连接 ,则 长的最大值与最小值的和是 .
15.圆与线段只有一个交点时,圆与线段不一定相切在Rt中,,若以为圆心,为半径的圆与斜边AB只有一个公共点,则的取值范围为 .
16.如图,OA在 x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,P的圆心P 在线段BC上,且P与边AB,AO都相切.若反比例函数(k≠0)的图象经过圆心P,则k= .
三、计算题
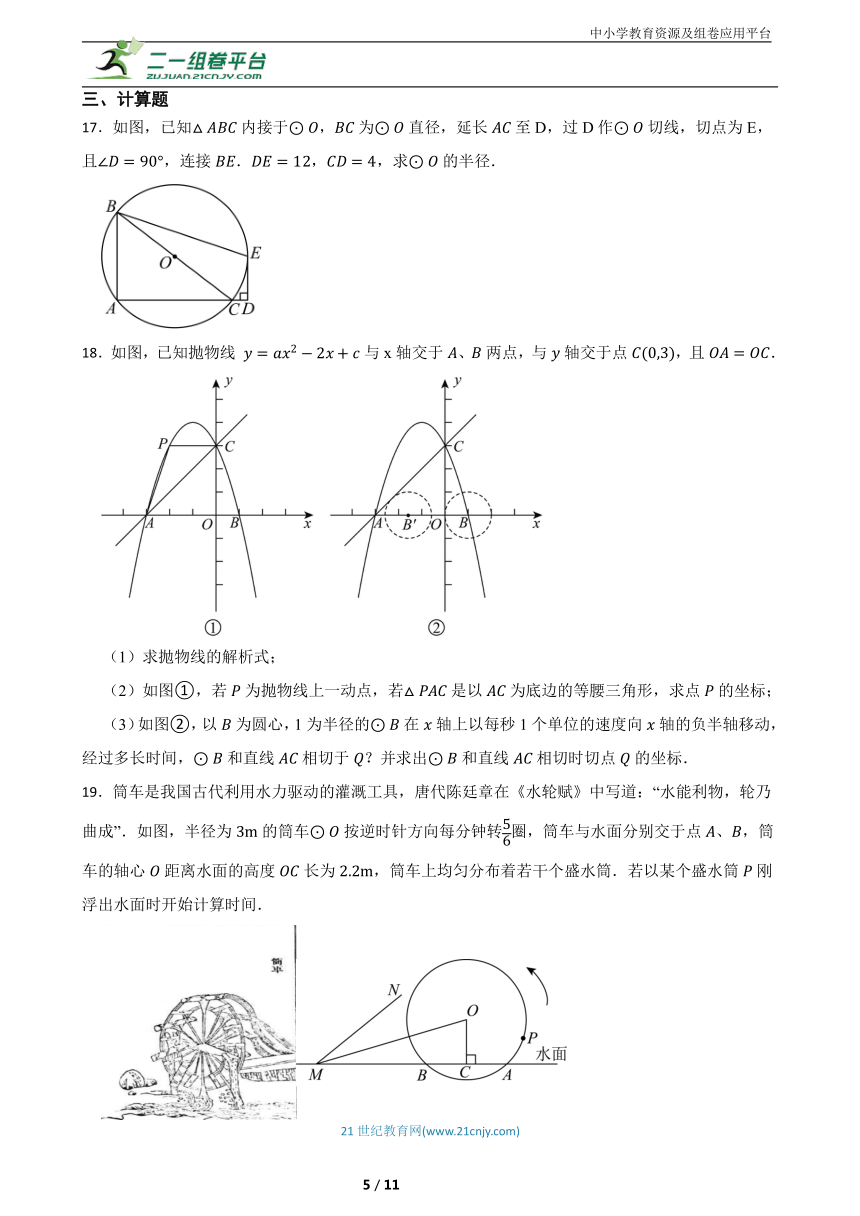
17.如图,已知内接于,为直径,延长至D,过D作切线,切点为E,且,连接.,,求的半径.
18.如图,已知抛物线 与x轴交于、两点,与轴交于点,且.
(1)求抛物线的解析式;
(2)如图①,若为抛物线上一动点,若是以为底边的等腰三角形,求点的坐标;
(3)如图②,以为圆心,1为半径的在轴上以每秒1个单位的速度向轴的负半轴移动,经过多长时间,和直线相切于?并求出和直线相切时切点的坐标.
19.筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点、,筒车的轴心距离水面的高度长为,筒车上均匀分布着若干个盛水筒.若以某个盛水筒刚浮出水面时开始计算时间.
(1)经过多长时间,盛水筒首次到达最高点?
(2)浮出水面3.4秒后,盛水筒距离水面多高?
(3)若接水槽所在直线是的切线,且与直线交于点,.求盛水筒从最高点开始,至少经过多长时间恰好在直线上.(参考数据:,,)
四、解答题
20.如图,是⊙O的直径,点E为⊙O上一点,和过E的切线互相垂直,垂足为D,切线交的延长线于点C.
(1)若,求的度数;
(2)若,求的长.
21.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
22.已知内接于,直线与相切于点D,且,连接.
(1)如图①,若,求的大小;
(2)如图②,的直径为4,若,求和的长.
23.如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
答案解析部分
1.【答案】C
【知识点】等腰三角形的性质;切线的性质
2.【答案】A
【知识点】圆周角定理;切线的性质
3.【答案】B
【知识点】直线与圆的位置关系
4.【答案】D
【知识点】直线与圆的位置关系
5.【答案】B
【知识点】勾股定理;直线与圆的位置关系;解直角三角形
6.【答案】A
【知识点】切线的性质;切线长定理
7.【答案】D
【知识点】勾股定理的应用;垂径定理的实际应用;切线的性质
8.【答案】A
【知识点】坐标与图形性质;直线与圆的位置关系
9.【答案】D
【知识点】切线的性质;二次函数的实际应用-几何问题
10.【答案】C
【知识点】线段垂直平分线的性质;切线的判定;相似三角形的判定与性质;三角形的中位线定理
11.【答案】105
【知识点】切线的性质
12.【答案】
【知识点】圆周角定理;切线的性质
13.【答案】40°
【知识点】圆周角定理;切线的性质
14.【答案】9
【知识点】两点之间线段最短;切线的性质
15.【答案】 或R=
【知识点】三角形的面积;勾股定理;直线与圆的位置关系
16.【答案】-5
【知识点】切线的判定与性质;相似三角形的判定与性质
17.【答案】半径
【知识点】勾股定理;矩形的判定;切线的性质
18.【答案】(1)抛物线的解析式为
(2),
(3),
【知识点】待定系数法求二次函数解析式;等腰三角形的判定与性质;切线的性质
19.【答案】(1)27.4秒;(2)0.7m;(3)7.6秒
【知识点】切线的性质;求特殊角的三角函数值;解直角三角形
20.【答案】(1)
(2)
【知识点】切线的性质;解直角三角形
21.【答案】相切
【知识点】直线与圆的位置关系
22.【答案】(1)
(2),
【知识点】垂径定理;圆周角定理;切线的性质;解直角三角形
23.【答案】(1)如图所示:
①以B为圆心,以任意长为半径画圆,分别交BC、AB于点G、H;②分别以G、H为圆心,以大于GH为半径画圆,两圆相交于D,连接BD;③过X作OX⊥AB,交直线BD于点O,则点O即为⊙O的圆心.
(2)①当⊙P与Rt△ABC的边AB和BC相切时,由角平分线的性质可知,动点P是∠ABC的平分线BM上的点,如图1,在∠ABC的平分线BM上任意确定点P1(不为∠ABC的顶点)
∵OX=BOsin∠ABM,P1Z=BPsin∠ABM,当BP1>BO时,P1Z>OX即P与B的距离越大,⊙P的面积越大,这时,BM与AC的交点P是符合题意的、BP长度最大的点; 如图2,
∵∠BPA>90°,过点P作PE⊥AB,垂足为E,则E在边AB上,
∴以P为圆心、PC为半径作圆,则⊙P与CB相切于C,与边AB相切于E,即这时⊙P是符合题意的圆,
时⊙P的面积就是S的最大值,
∵AC=1,BC=2,∴AB=,
设PC=x,则PA=AC-PC=1-x
在直角△APE中,PA2=PE2+AE2,
∴(1-x)2=x2+(-2)2,
∴x=2-4;
②如图3,
同理可得:当⊙P与Rt△ABC的边AB和AC相切时,设PC=y,则(2-y)2=y2+(-1)2,
∴y=;
③如图4,
同理可得,当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,
∵△APF∽△PBE,
∴PF:BE=AF:PE,
∴,
∴z=.
由①、②、③可知,
>>
∴z>y>x,
∴⊙P的面积S的最大值为π.
【知识点】切线的性质
21世纪教育网(www.21cnjy.com)
2 / 11
24.4直线与圆的位置关系本节综合题
一、单选题
1.如图,为的直径,是的切线,切点为,连接,若,则的度数为( )
A. B. C. D.
2.如图,AB是的直径,过点A作的切线,连接,与交于点D,E是上一点,连接.若,则的度数为( )
A. B. C. D.
3.已如⊙O的半径等于3,圈心O到直线l的距离为5,那么直线l与⊙O的位置关系是 ( )
A.直线l与⊙O相交 B.直线l与⊙O相离
C.直线l与⊙O相切 D.无法确定
4.在平面直角坐标系中,的半径是2,点在y轴上移动,当与x轴相交时,m的取值范围是( )
A. B.
C.或 D.
5.如图,中,,,,以点为圆心,为半径作,当时,与的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
6.如图,、、是的切线,点、、是切点,分别交、于、两点,若,则的度数( )
A. B. C. D.
7.如图,在平面直角坐标系中,与轴相切于原点,平行于轴的直线交于两点,若点的坐标是,则点的坐标为( )
A. B. C. D.
8.平面直角坐标系中,⊙P的圆心坐标为(-4,-5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
9.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
10.如图,线段是的直径,交线段于,且是中点,于,连接,则下列结论正确的个数是( )
;;;是的切线;.
A.2个 B.3个 C.4个 D.5个
二、填空题
11.如图,在△ABC中,AB=2,AC=,以A为圆心,1为半径的圆与边BC相切,则∠BAC的度数是 度.
12.如图,点A,B,C在上,且,,是切线,则为 度.
13.如图,为的切线点A为切点,交于点C,点D在上,连接、、,若,则的度数为 .
14.在 中, , ,以边 的中点 为圆心,作半圆与 相切,点 分别是边 和半圆上的动点,连接 ,则 长的最大值与最小值的和是 .
15.圆与线段只有一个交点时,圆与线段不一定相切在Rt中,,若以为圆心,为半径的圆与斜边AB只有一个公共点,则的取值范围为 .
16.如图,OA在 x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,P的圆心P 在线段BC上,且P与边AB,AO都相切.若反比例函数(k≠0)的图象经过圆心P,则k= .
三、计算题
17.如图,已知内接于,为直径,延长至D,过D作切线,切点为E,且,连接.,,求的半径.
18.如图,已知抛物线 与x轴交于、两点,与轴交于点,且.
(1)求抛物线的解析式;
(2)如图①,若为抛物线上一动点,若是以为底边的等腰三角形,求点的坐标;
(3)如图②,以为圆心,1为半径的在轴上以每秒1个单位的速度向轴的负半轴移动,经过多长时间,和直线相切于?并求出和直线相切时切点的坐标.
19.筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点、,筒车的轴心距离水面的高度长为,筒车上均匀分布着若干个盛水筒.若以某个盛水筒刚浮出水面时开始计算时间.
(1)经过多长时间,盛水筒首次到达最高点?
(2)浮出水面3.4秒后,盛水筒距离水面多高?
(3)若接水槽所在直线是的切线,且与直线交于点,.求盛水筒从最高点开始,至少经过多长时间恰好在直线上.(参考数据:,,)
四、解答题
20.如图,是⊙O的直径,点E为⊙O上一点,和过E的切线互相垂直,垂足为D,切线交的延长线于点C.
(1)若,求的度数;
(2)若,求的长.
21.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
22.已知内接于,直线与相切于点D,且,连接.
(1)如图①,若,求的大小;
(2)如图②,的直径为4,若,求和的长.
23.如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
答案解析部分
1.【答案】C
【知识点】等腰三角形的性质;切线的性质
2.【答案】A
【知识点】圆周角定理;切线的性质
3.【答案】B
【知识点】直线与圆的位置关系
4.【答案】D
【知识点】直线与圆的位置关系
5.【答案】B
【知识点】勾股定理;直线与圆的位置关系;解直角三角形
6.【答案】A
【知识点】切线的性质;切线长定理
7.【答案】D
【知识点】勾股定理的应用;垂径定理的实际应用;切线的性质
8.【答案】A
【知识点】坐标与图形性质;直线与圆的位置关系
9.【答案】D
【知识点】切线的性质;二次函数的实际应用-几何问题
10.【答案】C
【知识点】线段垂直平分线的性质;切线的判定;相似三角形的判定与性质;三角形的中位线定理
11.【答案】105
【知识点】切线的性质
12.【答案】
【知识点】圆周角定理;切线的性质
13.【答案】40°
【知识点】圆周角定理;切线的性质
14.【答案】9
【知识点】两点之间线段最短;切线的性质
15.【答案】 或R=
【知识点】三角形的面积;勾股定理;直线与圆的位置关系
16.【答案】-5
【知识点】切线的判定与性质;相似三角形的判定与性质
17.【答案】半径
【知识点】勾股定理;矩形的判定;切线的性质
18.【答案】(1)抛物线的解析式为
(2),
(3),
【知识点】待定系数法求二次函数解析式;等腰三角形的判定与性质;切线的性质
19.【答案】(1)27.4秒;(2)0.7m;(3)7.6秒
【知识点】切线的性质;求特殊角的三角函数值;解直角三角形
20.【答案】(1)
(2)
【知识点】切线的性质;解直角三角形
21.【答案】相切
【知识点】直线与圆的位置关系
22.【答案】(1)
(2),
【知识点】垂径定理;圆周角定理;切线的性质;解直角三角形
23.【答案】(1)如图所示:
①以B为圆心,以任意长为半径画圆,分别交BC、AB于点G、H;②分别以G、H为圆心,以大于GH为半径画圆,两圆相交于D,连接BD;③过X作OX⊥AB,交直线BD于点O,则点O即为⊙O的圆心.
(2)①当⊙P与Rt△ABC的边AB和BC相切时,由角平分线的性质可知,动点P是∠ABC的平分线BM上的点,如图1,在∠ABC的平分线BM上任意确定点P1(不为∠ABC的顶点)
∵OX=BOsin∠ABM,P1Z=BPsin∠ABM,当BP1>BO时,P1Z>OX即P与B的距离越大,⊙P的面积越大,这时,BM与AC的交点P是符合题意的、BP长度最大的点; 如图2,
∵∠BPA>90°,过点P作PE⊥AB,垂足为E,则E在边AB上,
∴以P为圆心、PC为半径作圆,则⊙P与CB相切于C,与边AB相切于E,即这时⊙P是符合题意的圆,
时⊙P的面积就是S的最大值,
∵AC=1,BC=2,∴AB=,
设PC=x,则PA=AC-PC=1-x
在直角△APE中,PA2=PE2+AE2,
∴(1-x)2=x2+(-2)2,
∴x=2-4;
②如图3,
同理可得:当⊙P与Rt△ABC的边AB和AC相切时,设PC=y,则(2-y)2=y2+(-1)2,
∴y=;
③如图4,
同理可得,当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,
∵△APF∽△PBE,
∴PF:BE=AF:PE,
∴,
∴z=.
由①、②、③可知,
>>
∴z>y>x,
∴⊙P的面积S的最大值为π.
【知识点】切线的性质
21世纪教育网(www.21cnjy.com)
2 / 11
