26.2.3概率在实际生活的应用 同步练习(含答案)
文档属性
| 名称 | 26.2.3概率在实际生活的应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 296.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 19:01:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
26.2.3概率在实际生活的应用
一、单选题
1.如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到6号卡片的概率是( )
A. B. C. D.
2.在一只不透明的口袋中放入除颜色外规格完全相同的白球个,黑球8个,黄球4个,搅匀后随机从中摸取一个恰好是白球的概率为,则的值为( )
A.4 B.5 C.6 D.7
3.在一次生活垃圾分类知识竞赛中,某校七、八年级各有100名学生参加,已知七年级男生成绩的优秀率为40%,女生成绩的优秀率为60%;八年级男生成绩的优秀率为50%,女生成绩的优秀率为70%对于此次竞赛的成绩,下面有三个推断:
①七年级男生成绩的优秀率小于八年级男生成绩的优秀率;②七年级学生成绩的优秀率一定小于八年级学生成绩的优秀率;③七、八年级所有男生成绩的优秀率一定小于七、八年级所有女生成绩的优秀率.
所有合理推断的序号是( )
A.①② B.①③ C.②③ D.①②③
4.下表所示为某种抽奖活动中,封闭的抽奖箱中各种球的颜色、数量以及它们所代表的奖项.为了保证抽奖的公平性,这些球除了颜色外其他均相同,而且每一个球被抽中的机会均相等,则该抽奖活动抽中一等奖的概率为( ).
颜色 数量(个) 奖项
红色 5 一等奖
黄色 6 二等奖
蓝色 9 三等奖
白色 10 四等奖
A. B. C. D.
5.在一个不透明的袋子中放有 个球,其中有6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0. 25左右,则 的值约为( )
A.10 B.15 C.20 D.24
6.某人将一枚质量分布均匀的硬币连续抛50次,落地后正面朝上30次,反面朝上20次,下列说法正确的是( )
A.出现正面的频率是30 B.出现正面的频率是20
C.出现正面的频率是0.6 D.出现正面的频率是0.4
7.一个密码箱的密码,每个位数上的数都是从0到9的自然数,若要使不知道密码的一次就拨对密码的概率小于 ,则密码的位数至少需要( )位.
A.3位 B.2位 C.9位 D.10位
8.袋中有五个小球,3个红球,2个白球,它们除了颜色外其余完全一样.现从中任意摸一个球.摸出红球的概率为( )
A. B. C. D.
9.小刚和小丽一起玩一种转盘游戏.转盘分成面积相等的三个区域,分别用“1”,“2”,“3”表示,固定指针转动转盘,任其自由停止.若指针所指的数字为奇数,小刚获胜;否则小丽获胜.此规则( )
A.公平 B.对小丽有利
C.对小刚有利 D.公平性不可预测
10.甲乙两人轮流在黑板上写下不超过 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A.10 B.9 C.8 D.6
二、填空题
11.标号分别为1,2,3,4,……,n的n张标签(除标号外其它完全相同),任摸一张,若摸得奇数号标签的概率大于0.5,则n可以是 .
12.不透明袋中装有个红球和个绿球,这些球除颜色外无其他差别.从袋中随机摸出个球是红球的概率为 .
13. 五一假期间,一家文具店购进了一纸箱除颜色外都相同的散装铅笔共支小红将纸箱里的铅笔搅匀后,从中随机摸出一支铅笔记下其颜色,把它放回箱子中;搅匀后再随机摸出一支铅笔记下其颜色,把它放回箱子中;,多次重复上述过程后,发现摸到黑色铅笔的频率逐渐稳定在左右,由此可以估计纸箱中黑色铅笔有 支
14.某人设摊“摸彩”,只见他手持一袋,内装大小、质量完全相同的3个红球、2个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得10元钱,否则顾客付给这人10元钱,请你判断一下该活动对顾客
(填“合算”或“不合算”).
15.国家卫健委高级别专家组组长、中国工程院院士钟南山表示,疫苗是解决新冠肺炎的根本。然而,疫苗研制需要过程,临床试验蕴含一定风险。现有甲、乙、丙三名志愿者要参加新冠疫苗临床试验,现只需选2人,甲被选中的概率为 。
16.一个密码箱的密码,每个数位上的数都是从0到9的自然数,若要使不知道密码的人一次就拨对密码的概率小于 ,则密码的位数至少需要 位.
三、计算题
17.在一个不透明的布袋里装有四个完全相同的小球,上面分别标有数字1 2 2 3.
(1)若小明随机抽出一个小球,求抽到标有数字2的小球的概率;
(2)小明先从口袋里随机不放回地取出一个小球,记下数字为x.小红再从剩下的三个小球中随机取出一个小球,记下数字为y,点Q坐标记作(x,y).规定:若点Q(x,y)在反比例函数图象上则小明胜;若点Q在反比例函数图象上,则小红胜.请你通过计算,判断这个游戏是否公平?
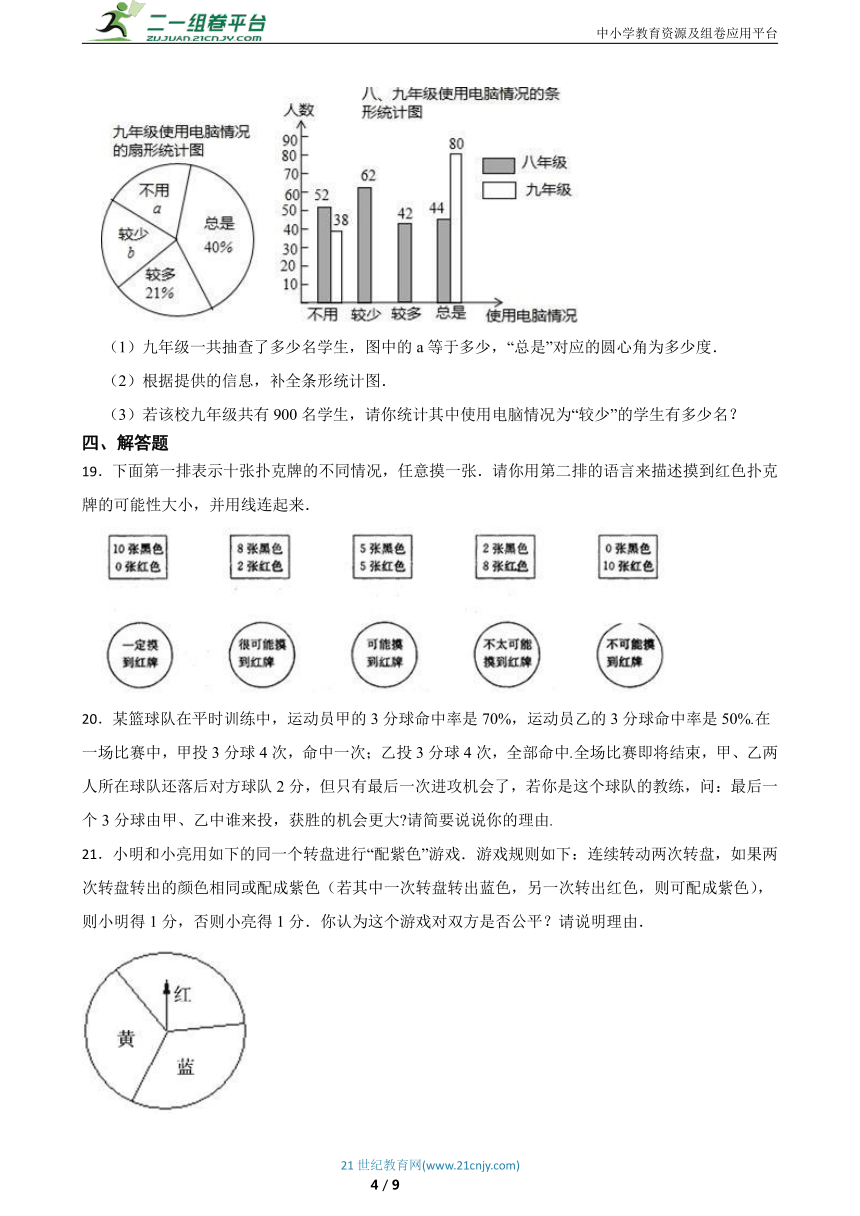
18.某校为了了解学生在家使用电脑的情况(分为“总是、较多、较少、不用”四种情况),随机在八、九年级各抽取相同数量的学生进行调查,绘制成部分统计图如下所示.请根据图中信息,回答下列问题:
(1)九年级一共抽查了多少名学生,图中的a等于多少,“总是”对应的圆心角为多少度.
(2)根据提供的信息,补全条形统计图.
(3)若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?
四、解答题
19.下面第一排表示十张扑克牌的不同情况,任意摸一张.请你用第二排的语言来描述摸到红色扑克牌的可能性大小,并用线连起来.
20.某篮球队在平时训练中,运动员甲的3分球命中率是70%,运动员乙的3分球命中率是50%.在一场比赛中,甲投3分球4次,命中一次;乙投3分球4次,全部命中.全场比赛即将结束,甲、乙两人所在球队还落后对方球队2分,但只有最后一次进攻机会了,若你是这个球队的教练,问:最后一个3分球由甲、乙中谁来投,获胜的机会更大 请简要说说你的理由.
21.小明和小亮用如下的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方是否公平?请说明理由.
22.已知甲同学手中藏有三张分别标有数字,,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲、乙两人手中各任取一张卡片,并将它们的数字分别记为.
(1)请你用画树状图或列表的方法列出所有可能的结果.
(2)现制订这样一个游戏规则:若所选出的能使得有两个不相等的实数根,则称甲获胜;否则称乙获胜.请问:这样的游戏规则公平吗 请你用概率的知识解释.
答案解析部分
1.【答案】B
【知识点】概率的简单应用
2.【答案】C
【知识点】概率公式;概率的简单应用
3.【答案】B
【知识点】常用统计量的选择;概率的简单应用
4.【答案】A
【知识点】概率的简单应用
5.【答案】D
【知识点】概率的简单应用
6.【答案】C
【知识点】概率的简单应用
7.【答案】A
【知识点】概率公式;概率的简单应用
8.【答案】C
【知识点】概率的简单应用
9.【答案】C
【知识点】游戏公平性
10.【答案】D
【知识点】游戏公平性
11.【答案】奇数
【知识点】概率的简单应用
12.【答案】
【知识点】概率的简单应用
13.【答案】
【知识点】概率的简单应用
14.【答案】不合算
【知识点】游戏公平性
15.【答案】
【知识点】概率的简单应用
16.【答案】4
【知识点】概率的简单应用
17.【答案】(1);(2)公平
【知识点】待定系数法求一次函数解析式;用列表法或树状图法求概率;游戏公平性
18.【答案】(1)九年级一共抽查了80÷40%=200名学生, ,所以图中的a=19%,“总是”对应的圆心角为360°×40%=144度;
(2)较多:200×21%=42(名),
较少:200-(38+42+80)=40(名),
如图所示;
(3) ×100%=20%,
900×20%=180(人)
答:使用电脑情况为“较少”的学生有180名.
【知识点】扇形统计图;条形统计图;概率公式;概率的简单应用
19.【答案】解:10张黑色0张红色,不可能摸到红牌;8张黑色2张红色,不太可能摸到红牌;5张黑色5张红色,可能摸到红牌;2张黑色8张红色,很可能摸到红牌;0张黑色10张红色,一定摸到红牌.
【知识点】概率的简单应用
20.【答案】解:由于甲的命中率高,所以由甲投;由于乙本场发挥稳定,命中率为100%,故可由乙投.
【知识点】概率的简单应用
21.【答案】
第二次第一次 红 黄 蓝
红 (红,红) (红,黄) (红,蓝)
黄 (黄,红) (黄,黄) (黄,蓝)
蓝 (蓝,红) (蓝,黄) (蓝,蓝)
从表中可以得到:P(小明获胜)=,P(小亮获胜)=.∴小明的得分为×1=,小亮的得分为×1=.∵>,∴游戏不公平.
【知识点】游戏公平性
22.【答案】(1)解:画树状图如下,
由树状图可知:(a,b)所有可能的结果数为:,,,,,,(1,1),(1,3),(1,2)共9种;
(2)解:不公平,理由如下:
∵所选出的a、b能使ax2+bx+1=0有两个不相等的实数根,
∴△=b2-4ac>0,即b2-4a>0,
而当a=,b=1时,b2-4a=-1<0,
当a=,b=3时,b2-4a=7>0,
当a=,b=2时,b2-4a=2>0,
当a=,b=1时,b2-4a=0,
当a=,b=3时,b2-4a=8>0,
当a=,b=2时,b2-4a=3>0,
当a=1,b=1时,b2-4a=-3<0,
当a=1,b=3时,b2-4a=5>0,
当a=1,b=2时,b2-4a=0,
∴(甲获胜),P(乙获胜),
而,所以这样的游戏规则对甲有利,不公平.
【知识点】一元二次方程根的判别式及应用;用列表法或树状图法求概率;游戏公平性
21世纪教育网(www.21cnjy.com)
1 / 9
26.2.3概率在实际生活的应用
一、单选题
1.如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到6号卡片的概率是( )
A. B. C. D.
2.在一只不透明的口袋中放入除颜色外规格完全相同的白球个,黑球8个,黄球4个,搅匀后随机从中摸取一个恰好是白球的概率为,则的值为( )
A.4 B.5 C.6 D.7
3.在一次生活垃圾分类知识竞赛中,某校七、八年级各有100名学生参加,已知七年级男生成绩的优秀率为40%,女生成绩的优秀率为60%;八年级男生成绩的优秀率为50%,女生成绩的优秀率为70%对于此次竞赛的成绩,下面有三个推断:
①七年级男生成绩的优秀率小于八年级男生成绩的优秀率;②七年级学生成绩的优秀率一定小于八年级学生成绩的优秀率;③七、八年级所有男生成绩的优秀率一定小于七、八年级所有女生成绩的优秀率.
所有合理推断的序号是( )
A.①② B.①③ C.②③ D.①②③
4.下表所示为某种抽奖活动中,封闭的抽奖箱中各种球的颜色、数量以及它们所代表的奖项.为了保证抽奖的公平性,这些球除了颜色外其他均相同,而且每一个球被抽中的机会均相等,则该抽奖活动抽中一等奖的概率为( ).
颜色 数量(个) 奖项
红色 5 一等奖
黄色 6 二等奖
蓝色 9 三等奖
白色 10 四等奖
A. B. C. D.
5.在一个不透明的袋子中放有 个球,其中有6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0. 25左右,则 的值约为( )
A.10 B.15 C.20 D.24
6.某人将一枚质量分布均匀的硬币连续抛50次,落地后正面朝上30次,反面朝上20次,下列说法正确的是( )
A.出现正面的频率是30 B.出现正面的频率是20
C.出现正面的频率是0.6 D.出现正面的频率是0.4
7.一个密码箱的密码,每个位数上的数都是从0到9的自然数,若要使不知道密码的一次就拨对密码的概率小于 ,则密码的位数至少需要( )位.
A.3位 B.2位 C.9位 D.10位
8.袋中有五个小球,3个红球,2个白球,它们除了颜色外其余完全一样.现从中任意摸一个球.摸出红球的概率为( )
A. B. C. D.
9.小刚和小丽一起玩一种转盘游戏.转盘分成面积相等的三个区域,分别用“1”,“2”,“3”表示,固定指针转动转盘,任其自由停止.若指针所指的数字为奇数,小刚获胜;否则小丽获胜.此规则( )
A.公平 B.对小丽有利
C.对小刚有利 D.公平性不可预测
10.甲乙两人轮流在黑板上写下不超过 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A.10 B.9 C.8 D.6
二、填空题
11.标号分别为1,2,3,4,……,n的n张标签(除标号外其它完全相同),任摸一张,若摸得奇数号标签的概率大于0.5,则n可以是 .
12.不透明袋中装有个红球和个绿球,这些球除颜色外无其他差别.从袋中随机摸出个球是红球的概率为 .
13. 五一假期间,一家文具店购进了一纸箱除颜色外都相同的散装铅笔共支小红将纸箱里的铅笔搅匀后,从中随机摸出一支铅笔记下其颜色,把它放回箱子中;搅匀后再随机摸出一支铅笔记下其颜色,把它放回箱子中;,多次重复上述过程后,发现摸到黑色铅笔的频率逐渐稳定在左右,由此可以估计纸箱中黑色铅笔有 支
14.某人设摊“摸彩”,只见他手持一袋,内装大小、质量完全相同的3个红球、2个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得10元钱,否则顾客付给这人10元钱,请你判断一下该活动对顾客
(填“合算”或“不合算”).
15.国家卫健委高级别专家组组长、中国工程院院士钟南山表示,疫苗是解决新冠肺炎的根本。然而,疫苗研制需要过程,临床试验蕴含一定风险。现有甲、乙、丙三名志愿者要参加新冠疫苗临床试验,现只需选2人,甲被选中的概率为 。
16.一个密码箱的密码,每个数位上的数都是从0到9的自然数,若要使不知道密码的人一次就拨对密码的概率小于 ,则密码的位数至少需要 位.
三、计算题
17.在一个不透明的布袋里装有四个完全相同的小球,上面分别标有数字1 2 2 3.
(1)若小明随机抽出一个小球,求抽到标有数字2的小球的概率;
(2)小明先从口袋里随机不放回地取出一个小球,记下数字为x.小红再从剩下的三个小球中随机取出一个小球,记下数字为y,点Q坐标记作(x,y).规定:若点Q(x,y)在反比例函数图象上则小明胜;若点Q在反比例函数图象上,则小红胜.请你通过计算,判断这个游戏是否公平?
18.某校为了了解学生在家使用电脑的情况(分为“总是、较多、较少、不用”四种情况),随机在八、九年级各抽取相同数量的学生进行调查,绘制成部分统计图如下所示.请根据图中信息,回答下列问题:
(1)九年级一共抽查了多少名学生,图中的a等于多少,“总是”对应的圆心角为多少度.
(2)根据提供的信息,补全条形统计图.
(3)若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?
四、解答题
19.下面第一排表示十张扑克牌的不同情况,任意摸一张.请你用第二排的语言来描述摸到红色扑克牌的可能性大小,并用线连起来.
20.某篮球队在平时训练中,运动员甲的3分球命中率是70%,运动员乙的3分球命中率是50%.在一场比赛中,甲投3分球4次,命中一次;乙投3分球4次,全部命中.全场比赛即将结束,甲、乙两人所在球队还落后对方球队2分,但只有最后一次进攻机会了,若你是这个球队的教练,问:最后一个3分球由甲、乙中谁来投,获胜的机会更大 请简要说说你的理由.
21.小明和小亮用如下的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方是否公平?请说明理由.
22.已知甲同学手中藏有三张分别标有数字,,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲、乙两人手中各任取一张卡片,并将它们的数字分别记为.
(1)请你用画树状图或列表的方法列出所有可能的结果.
(2)现制订这样一个游戏规则:若所选出的能使得有两个不相等的实数根,则称甲获胜;否则称乙获胜.请问:这样的游戏规则公平吗 请你用概率的知识解释.
答案解析部分
1.【答案】B
【知识点】概率的简单应用
2.【答案】C
【知识点】概率公式;概率的简单应用
3.【答案】B
【知识点】常用统计量的选择;概率的简单应用
4.【答案】A
【知识点】概率的简单应用
5.【答案】D
【知识点】概率的简单应用
6.【答案】C
【知识点】概率的简单应用
7.【答案】A
【知识点】概率公式;概率的简单应用
8.【答案】C
【知识点】概率的简单应用
9.【答案】C
【知识点】游戏公平性
10.【答案】D
【知识点】游戏公平性
11.【答案】奇数
【知识点】概率的简单应用
12.【答案】
【知识点】概率的简单应用
13.【答案】
【知识点】概率的简单应用
14.【答案】不合算
【知识点】游戏公平性
15.【答案】
【知识点】概率的简单应用
16.【答案】4
【知识点】概率的简单应用
17.【答案】(1);(2)公平
【知识点】待定系数法求一次函数解析式;用列表法或树状图法求概率;游戏公平性
18.【答案】(1)九年级一共抽查了80÷40%=200名学生, ,所以图中的a=19%,“总是”对应的圆心角为360°×40%=144度;
(2)较多:200×21%=42(名),
较少:200-(38+42+80)=40(名),
如图所示;
(3) ×100%=20%,
900×20%=180(人)
答:使用电脑情况为“较少”的学生有180名.
【知识点】扇形统计图;条形统计图;概率公式;概率的简单应用
19.【答案】解:10张黑色0张红色,不可能摸到红牌;8张黑色2张红色,不太可能摸到红牌;5张黑色5张红色,可能摸到红牌;2张黑色8张红色,很可能摸到红牌;0张黑色10张红色,一定摸到红牌.
【知识点】概率的简单应用
20.【答案】解:由于甲的命中率高,所以由甲投;由于乙本场发挥稳定,命中率为100%,故可由乙投.
【知识点】概率的简单应用
21.【答案】
第二次第一次 红 黄 蓝
红 (红,红) (红,黄) (红,蓝)
黄 (黄,红) (黄,黄) (黄,蓝)
蓝 (蓝,红) (蓝,黄) (蓝,蓝)
从表中可以得到:P(小明获胜)=,P(小亮获胜)=.∴小明的得分为×1=,小亮的得分为×1=.∵>,∴游戏不公平.
【知识点】游戏公平性
22.【答案】(1)解:画树状图如下,
由树状图可知:(a,b)所有可能的结果数为:,,,,,,(1,1),(1,3),(1,2)共9种;
(2)解:不公平,理由如下:
∵所选出的a、b能使ax2+bx+1=0有两个不相等的实数根,
∴△=b2-4ac>0,即b2-4a>0,
而当a=,b=1时,b2-4a=-1<0,
当a=,b=3时,b2-4a=7>0,
当a=,b=2时,b2-4a=2>0,
当a=,b=1时,b2-4a=0,
当a=,b=3时,b2-4a=8>0,
当a=,b=2时,b2-4a=3>0,
当a=1,b=1时,b2-4a=-3<0,
当a=1,b=3时,b2-4a=5>0,
当a=1,b=2时,b2-4a=0,
∴(甲获胜),P(乙获胜),
而,所以这样的游戏规则对甲有利,不公平.
【知识点】一元二次方程根的判别式及应用;用列表法或树状图法求概率;游戏公平性
21世纪教育网(www.21cnjy.com)
1 / 9
