平方差公式因式分解
图片预览



文档简介
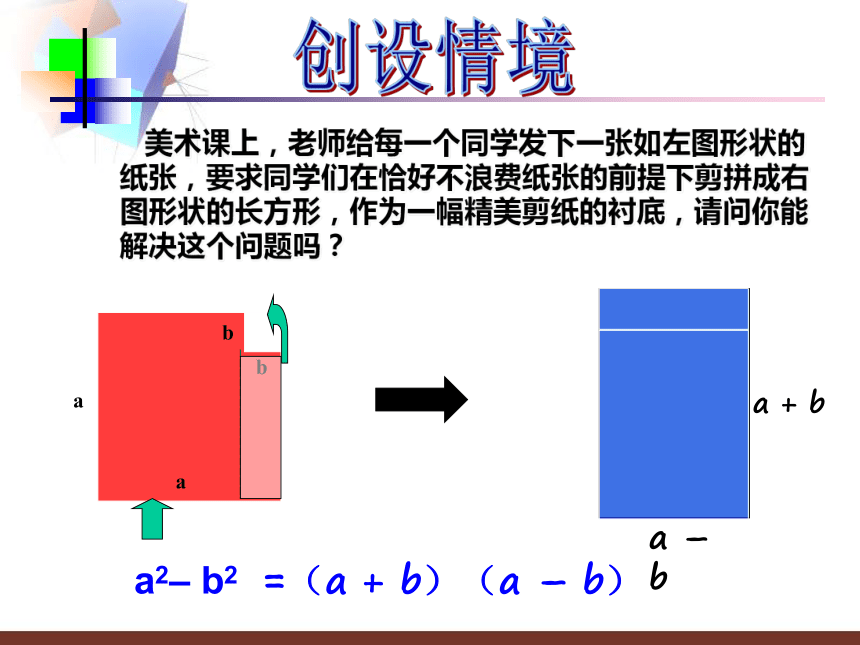
课件15张PPT。运用公式法—平方差公式 长明中学 秦海燕美术课上,老师给每一个同学发下一张如左图形状的纸张,要求同学们在恰好不浪费纸张的前提下剪拼成右图形状的长方形,作为一幅精美剪纸的衬底,请问你能解决这个问题吗?=(a + b)(a – b)a2– b2创设情境a2 - b2 = (a+b)(a-b)
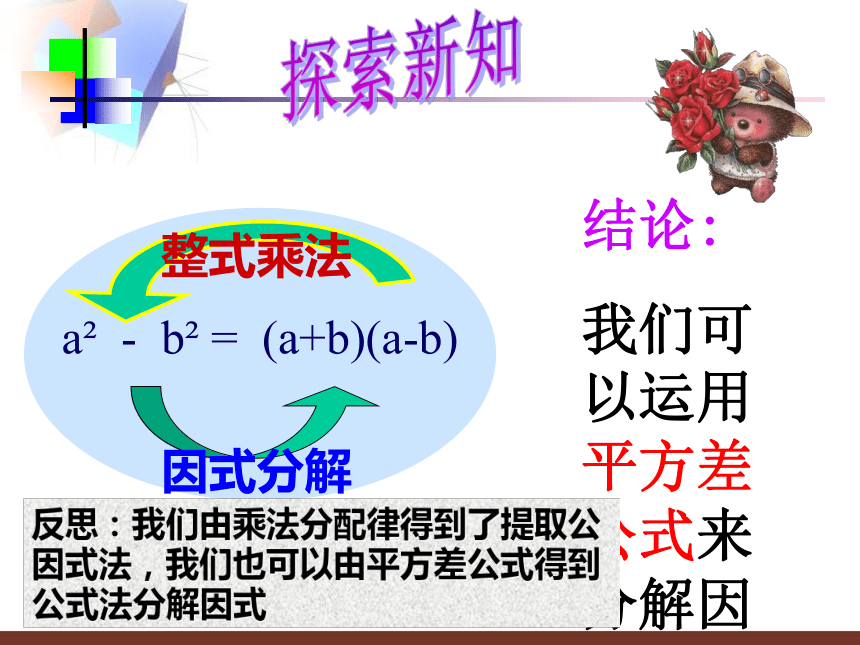
因式分解整式乘法结论:
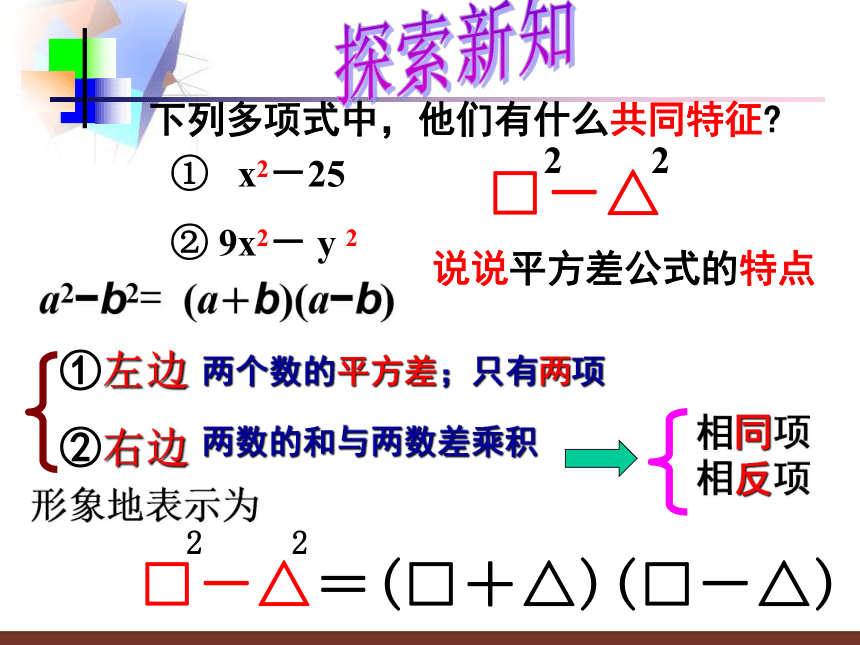
我们可以运用平方差公式来分解因式反思:我们由乘法分配律得到了提取公因式法,我们也可以由平方差公式得到公式法分解因式探索新知a2?b2= (a+b)(a?b)说说平方差公式的特点两数的和与两数差乘积两个数的平方差;只有两项 形象地表示为 下列多项式中,他们有什么共同特征? ① x2-25
② 9x2- y 2 探索新知在多项式x2+y2, x2-y2 ,-x2+y2, -x2-y2中,能利用平方差公式分解的有( )
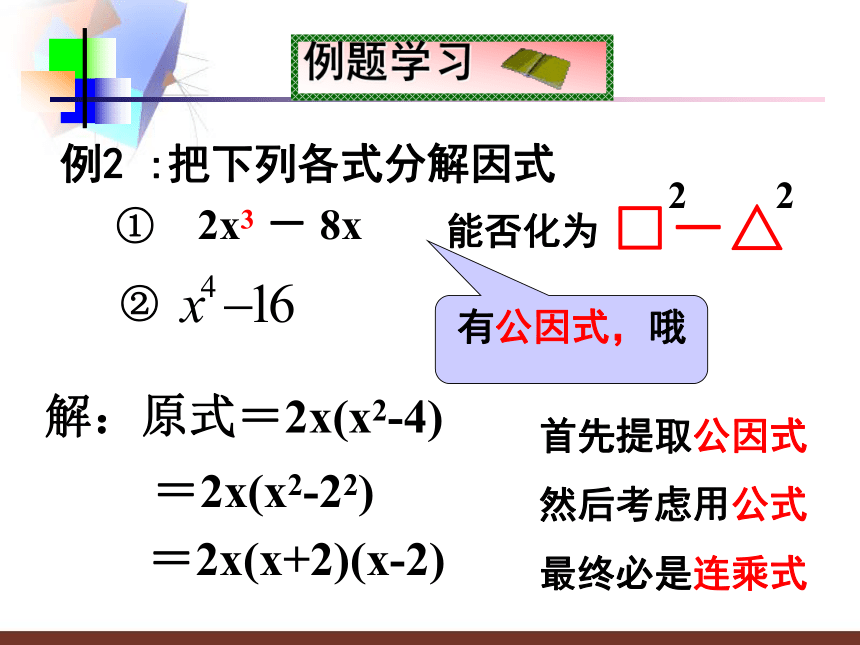
A 1个 B 2个 C 3个 D 4个B如果一个多项式能写成两个数的平方差的形式,那么就可以运用平方差形式把它因式分解,等于两个数的和与这两个数的差的乘积。探索新知a2?b2= (a+b)(a?b)例1、把下列各式分解因式:(1) 25 - 16x2(3) - 16x2 +81y2解(1)原式= 52-(4x)2=(5+4x)(5-4x)(4) 公式中a、b可以是单独的数或字母,也可以是单项式或多项式。 例题学习 例题学习 例2 :把下列各式分解因式首先提取公因式
然后考虑用公式
最终必是连乘式解:原式=2x(x2-4)=2x(x2-22)=2x(x+2)(x-2)有公因式,哦例题学习 解:因式分解要分解到不能再分解为止!(2)例题学习 例题3 利用平方差公式计算:解:运用平方差公式可以使计算简便。练习反馈,拓展思维把下列各式分解因式
(1) x2 - 1开始抢答(2) m2 - 9(3) x2 - 4y2=(x+1)(x-1)=(m+3)(m-3)=(x+2y)(x-2y)2、把下列各式分解因式:(1)9x2-4y2
(2)
(3)(3a+2b)2-(2a+3b)2练习反馈,拓展思维①运用a2?b2= (a+b)(a?b)分解因式首先提取公因式
然后考虑用公式
分解一定要彻底
最终必是连乘式②分解因式顺序归纳总结 巩固新知这节课你学会了什么?特点:(1)这个多项式是两项式(或可以看成两项);(2)每一项都能写成平方的形式;(3)两项的系数异号。思维拓展1.因式分解:(1)(2)2.你能说明 能被24整除吗?结束寄语一个人只要坚持不懈地追求,他就能达到目的. 再见欢 迎 莅 临 指 导 !欢 迎 莅 临 指 导 !欢 迎 莅 临 指 导 !
因式分解整式乘法结论:
我们可以运用平方差公式来分解因式反思:我们由乘法分配律得到了提取公因式法,我们也可以由平方差公式得到公式法分解因式探索新知a2?b2= (a+b)(a?b)说说平方差公式的特点两数的和与两数差乘积两个数的平方差;只有两项 形象地表示为 下列多项式中,他们有什么共同特征? ① x2-25
② 9x2- y 2 探索新知在多项式x2+y2, x2-y2 ,-x2+y2, -x2-y2中,能利用平方差公式分解的有( )
A 1个 B 2个 C 3个 D 4个B如果一个多项式能写成两个数的平方差的形式,那么就可以运用平方差形式把它因式分解,等于两个数的和与这两个数的差的乘积。探索新知a2?b2= (a+b)(a?b)例1、把下列各式分解因式:(1) 25 - 16x2(3) - 16x2 +81y2解(1)原式= 52-(4x)2=(5+4x)(5-4x)(4) 公式中a、b可以是单独的数或字母,也可以是单项式或多项式。 例题学习 例题学习 例2 :把下列各式分解因式首先提取公因式
然后考虑用公式
最终必是连乘式解:原式=2x(x2-4)=2x(x2-22)=2x(x+2)(x-2)有公因式,哦例题学习 解:因式分解要分解到不能再分解为止!(2)例题学习 例题3 利用平方差公式计算:解:运用平方差公式可以使计算简便。练习反馈,拓展思维把下列各式分解因式
(1) x2 - 1开始抢答(2) m2 - 9(3) x2 - 4y2=(x+1)(x-1)=(m+3)(m-3)=(x+2y)(x-2y)2、把下列各式分解因式:(1)9x2-4y2
(2)
(3)(3a+2b)2-(2a+3b)2练习反馈,拓展思维①运用a2?b2= (a+b)(a?b)分解因式首先提取公因式
然后考虑用公式
分解一定要彻底
最终必是连乘式②分解因式顺序归纳总结 巩固新知这节课你学会了什么?特点:(1)这个多项式是两项式(或可以看成两项);(2)每一项都能写成平方的形式;(3)两项的系数异号。思维拓展1.因式分解:(1)(2)2.你能说明 能被24整除吗?结束寄语一个人只要坚持不懈地追求,他就能达到目的. 再见欢 迎 莅 临 指 导 !欢 迎 莅 临 指 导 !欢 迎 莅 临 指 导 !
