人教版(2024)数学七年级上册 6.3.2 角的比较与运算 课件(共20张PPT)
文档属性
| 名称 | 人教版(2024)数学七年级上册 6.3.2 角的比较与运算 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 298.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 16:48:02 | ||
图片预览








文档简介
(共20张PPT)
6.3.2 角的比较与运算
学习目标
2.认识角的平分线及角的等分线,会画角的平分线.
学习重点
角的大小比较方法;认识角的平分线.
学习难点
角的和与差计算;角的平分线等有关的计算.
1.能比较角的大小,会计算角的和与差,并会用文字、图形和符号语言进行描述.
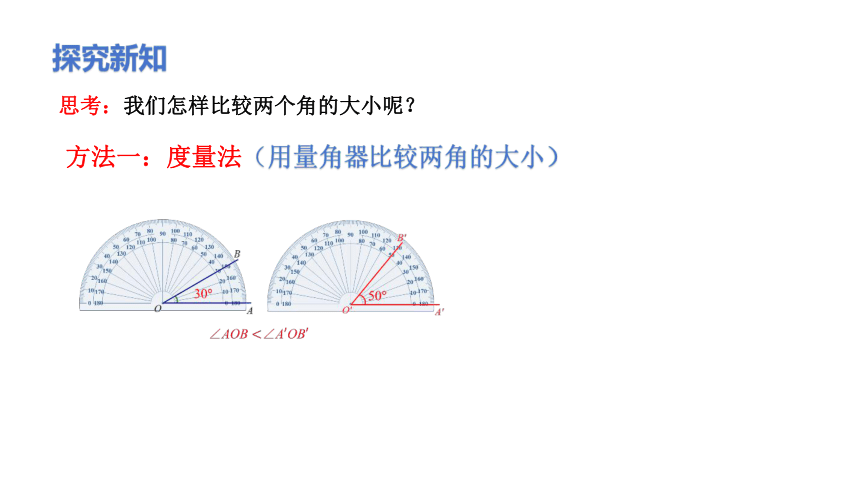
思考:我们怎样比较两个角的大小呢?
探究新知
方法一:度量法(用量角器比较两角的大小)
方法二:叠合法(将不同的角进行叠合)
∠AOB ∠AOB
∠AOB ∠AOB
∠AOB ∠AOB
探究新知
(1)将两个角的顶点及其中一条边重合.
(2)使两个角的另一边落在重合一边的同侧.
(3)根据两个角的另一边的位置关系确定两个角的大小.
叠合法比较两个角的大小的步骤:
探究新知
跟踪练习
1.在∠AOB的内部任取一点C,作射线OC,则下列结论一定正确的是( )
A.∠AOB >∠AOC
B.∠AOB =∠AOC
C.∠AOB <∠AOC
D.∠BOC >∠AOC
A
问题:如图所示,图中共有几个角?你能结合图说明什么是两个角的和与差吗?
图中共3个角,分别是∠AOB,∠BOC 和∠AOC
∠AOC是∠AOB与∠BOC的和,即:∠AOC=∠AOB+∠BOC,
∠AOB是∠AOC与∠BOC的差,即:∠AOB=∠AOC-∠BOC,
∠BOC是∠AOC与∠AOB的差,即:∠BOC=∠AOC-∠AOB.
探究新知
①两个角相加叫两个角的和,两个角相减叫两个角的差.
②进行角度的加、减运算时,要将度与度、分与分、秒与秒分别相加、减; 分、秒相加时,逢60要进位;相减不够时要借1作60.如例1中180°-53°17′应先将180°化为 179°60′,再进行相减.
探究新知
例:如图,O是直线AB上一点,∠AOC=53°17′,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
∠AOB=∠AOC+∠BOC,
所以∠BOC=∠AOB-∠AOC
=180°- 53 17′
=126°43′.
例题讲解
跟踪练习
1.如图∠AOB=90°,∠AOC=130°,则∠BOC的度数是( )
A.30°
B.40°
C.25°
D.50°
B
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC =∠AOB,
∠AOB =2∠BOC =2∠AOC.
探究新知
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
A
C
O
B
D
∵ ∠AOB =∠BOC=∠DOC
∴ OC 、OD是∠AOB 的三等分线
探究新知
例1 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7
= 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
例题讲解
例2 如图,O 是直线 AB 上一点,∠AOC=53°17′,OB 是∠BOC 的平分线,求∠DOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
D
例题讲解
课堂巩固
1.如图,把一块三角板的直角顶点B放在直线EF上,若∠2=35°,则∠2的度数是( )
A.30°
B.55°
C.65°
D.50°
B
课堂巩固
2.如图所示,
∠AOB=∠AOC-________.
∠AOD=∠AOB+_________.
∠BOC
∠DOB
课堂巩固
3.如图所示,OD平分∠AOC,若∠BOC=120°,则∠AOD=________.
30°
4.如图所示,∠BOC=2∠AOC,若∠AOC=40°,计算∠AOB的度数.
课堂巩固
解:由题意可知,∠BOC=2∠AOC
∠AOC=40°
所以∠BOC=80°
∠AOB=∠BOC+∠AOC=120°
5.计算
课堂巩固
(1)26°15′+32°20′
(2)90°-18°35′
解:(1)58°35′
(2)71°25′
角的比较与运算
比较
度量法
叠合法
数
形
和差
倍分
运算
A
B
O
C
A
C
O
B
A
C
O
B
D
课堂小结
6.3.2 角的比较与运算
学习目标
2.认识角的平分线及角的等分线,会画角的平分线.
学习重点
角的大小比较方法;认识角的平分线.
学习难点
角的和与差计算;角的平分线等有关的计算.
1.能比较角的大小,会计算角的和与差,并会用文字、图形和符号语言进行描述.
思考:我们怎样比较两个角的大小呢?
探究新知
方法一:度量法(用量角器比较两角的大小)
方法二:叠合法(将不同的角进行叠合)
∠AOB ∠AOB
∠AOB ∠AOB
∠AOB ∠AOB
探究新知
(1)将两个角的顶点及其中一条边重合.
(2)使两个角的另一边落在重合一边的同侧.
(3)根据两个角的另一边的位置关系确定两个角的大小.
叠合法比较两个角的大小的步骤:
探究新知
跟踪练习
1.在∠AOB的内部任取一点C,作射线OC,则下列结论一定正确的是( )
A.∠AOB >∠AOC
B.∠AOB =∠AOC
C.∠AOB <∠AOC
D.∠BOC >∠AOC
A
问题:如图所示,图中共有几个角?你能结合图说明什么是两个角的和与差吗?
图中共3个角,分别是∠AOB,∠BOC 和∠AOC
∠AOC是∠AOB与∠BOC的和,即:∠AOC=∠AOB+∠BOC,
∠AOB是∠AOC与∠BOC的差,即:∠AOB=∠AOC-∠BOC,
∠BOC是∠AOC与∠AOB的差,即:∠BOC=∠AOC-∠AOB.
探究新知
①两个角相加叫两个角的和,两个角相减叫两个角的差.
②进行角度的加、减运算时,要将度与度、分与分、秒与秒分别相加、减; 分、秒相加时,逢60要进位;相减不够时要借1作60.如例1中180°-53°17′应先将180°化为 179°60′,再进行相减.
探究新知
例:如图,O是直线AB上一点,∠AOC=53°17′,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
∠AOB=∠AOC+∠BOC,
所以∠BOC=∠AOB-∠AOC
=180°- 53 17′
=126°43′.
例题讲解
跟踪练习
1.如图∠AOB=90°,∠AOC=130°,则∠BOC的度数是( )
A.30°
B.40°
C.25°
D.50°
B
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC =∠AOB,
∠AOB =2∠BOC =2∠AOC.
探究新知
∵ ∠AOC =∠BOC
∴ OC 是∠AOB 的角平分线
A
C
O
B
A
C
O
B
D
∵ ∠AOB =∠BOC=∠DOC
∴ OC 、OD是∠AOB 的三等分线
探究新知
例1 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7
= 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
例题讲解
例2 如图,O 是直线 AB 上一点,∠AOC=53°17′,OB 是∠BOC 的平分线,求∠DOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
D
例题讲解
课堂巩固
1.如图,把一块三角板的直角顶点B放在直线EF上,若∠2=35°,则∠2的度数是( )
A.30°
B.55°
C.65°
D.50°
B
课堂巩固
2.如图所示,
∠AOB=∠AOC-________.
∠AOD=∠AOB+_________.
∠BOC
∠DOB
课堂巩固
3.如图所示,OD平分∠AOC,若∠BOC=120°,则∠AOD=________.
30°
4.如图所示,∠BOC=2∠AOC,若∠AOC=40°,计算∠AOB的度数.
课堂巩固
解:由题意可知,∠BOC=2∠AOC
∠AOC=40°
所以∠BOC=80°
∠AOB=∠BOC+∠AOC=120°
5.计算
课堂巩固
(1)26°15′+32°20′
(2)90°-18°35′
解:(1)58°35′
(2)71°25′
角的比较与运算
比较
度量法
叠合法
数
形
和差
倍分
运算
A
B
O
C
A
C
O
B
A
C
O
B
D
课堂小结
同课章节目录
