2024-2025学年人教版九年级上册数学期末能力提升测试题(含答案)
文档属性
| 名称 | 2024-2025学年人教版九年级上册数学期末能力提升测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 771.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 23:28:17 | ||
图片预览

文档简介
2024-2025学年人教版九年级上册数学期末能力提升测试题
一、单选题(共10题;共30分)
1.(3分)如图,某学校计划在一块长12米,宽9米的矩形空地修建两块形状大小相同的矩形种植园,它们的面积之和为60平方米,两块种植园之间及周边留有宽度相等的人行通道,若设人行通道的宽度为x米,则可以列出关于x的方程( )
A. B.
C. D.
2.(3分)如图,在平面直角坐标系中,四边形是菱形,,点坐标为,将菱形绕原点顺时针旋转,旋转后点的坐标为( )
A. B. C. D.
3.(3分)不透明的袋子里共装有2个黑球和3个白球,这些球除了颜色不同外,其余都完全相同,随机从袋子中摸出一个球,摸到黑球的概率是( )
A. B. C. D.
4.(3分)我国明代科学家徐光启在《农政全书》中描绘了一种我国古代常用的水利灌溉工具——筒车,如图,筒车盛水桶的运行轨道是以轴心为圆心的圆,已知圆心在水面的上方,的半径长为5米,被水面截得的弦长为8米,点是运行轨道的最低点,则点到弦的距离为( )
A.5米 B.4米 C.3米 D.2米
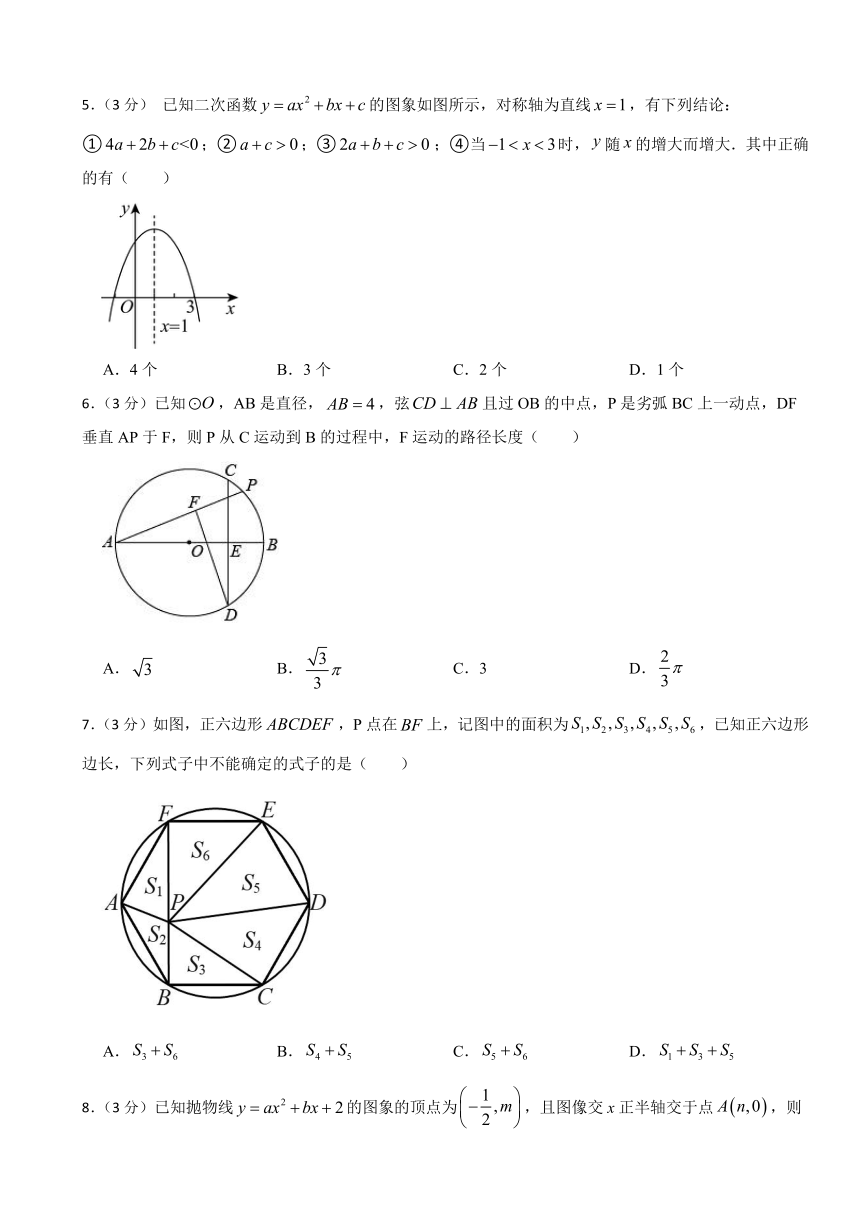
5.(3分) 已知二次函数的图象如图所示,对称轴为直线,有下列结论:①;②;③;④当时,随的增大而增大.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
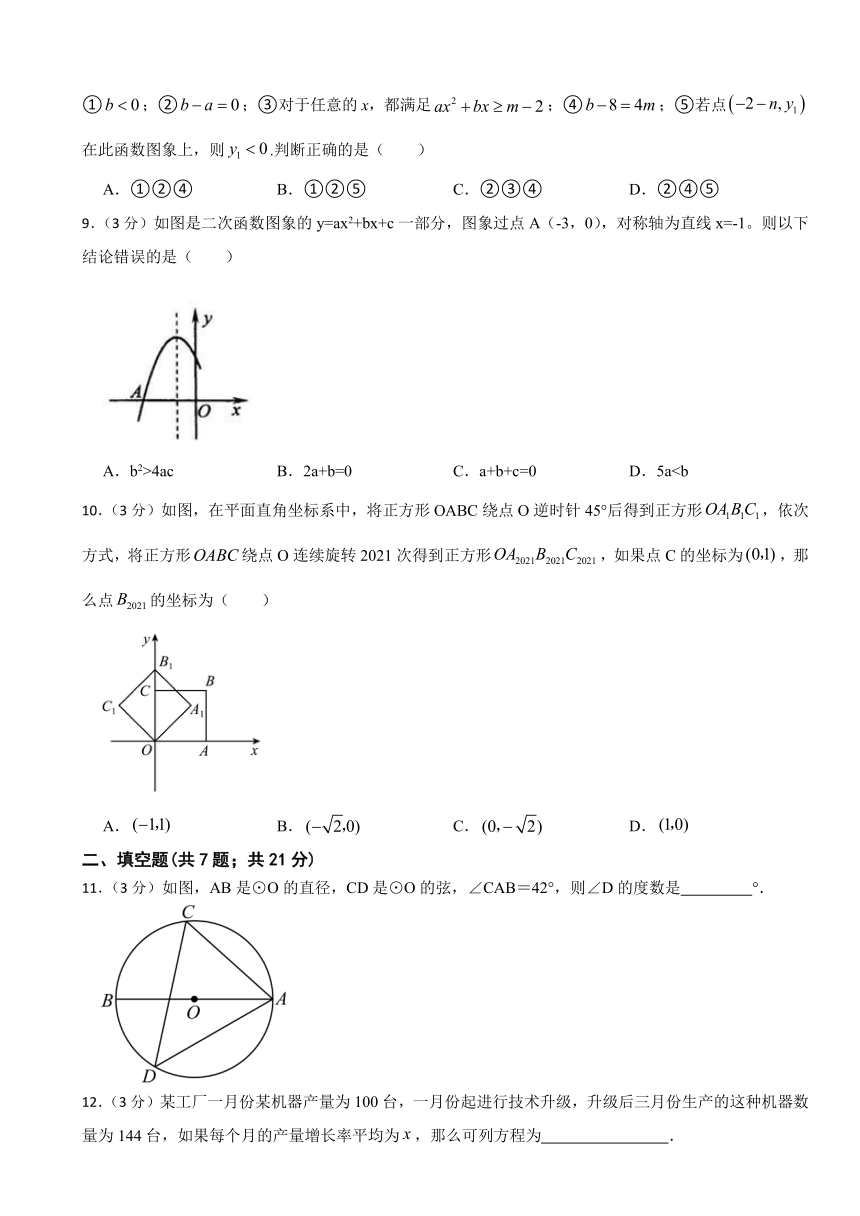
6.(3分)已知,AB是直径,,弦且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
A. B. C.3 D.
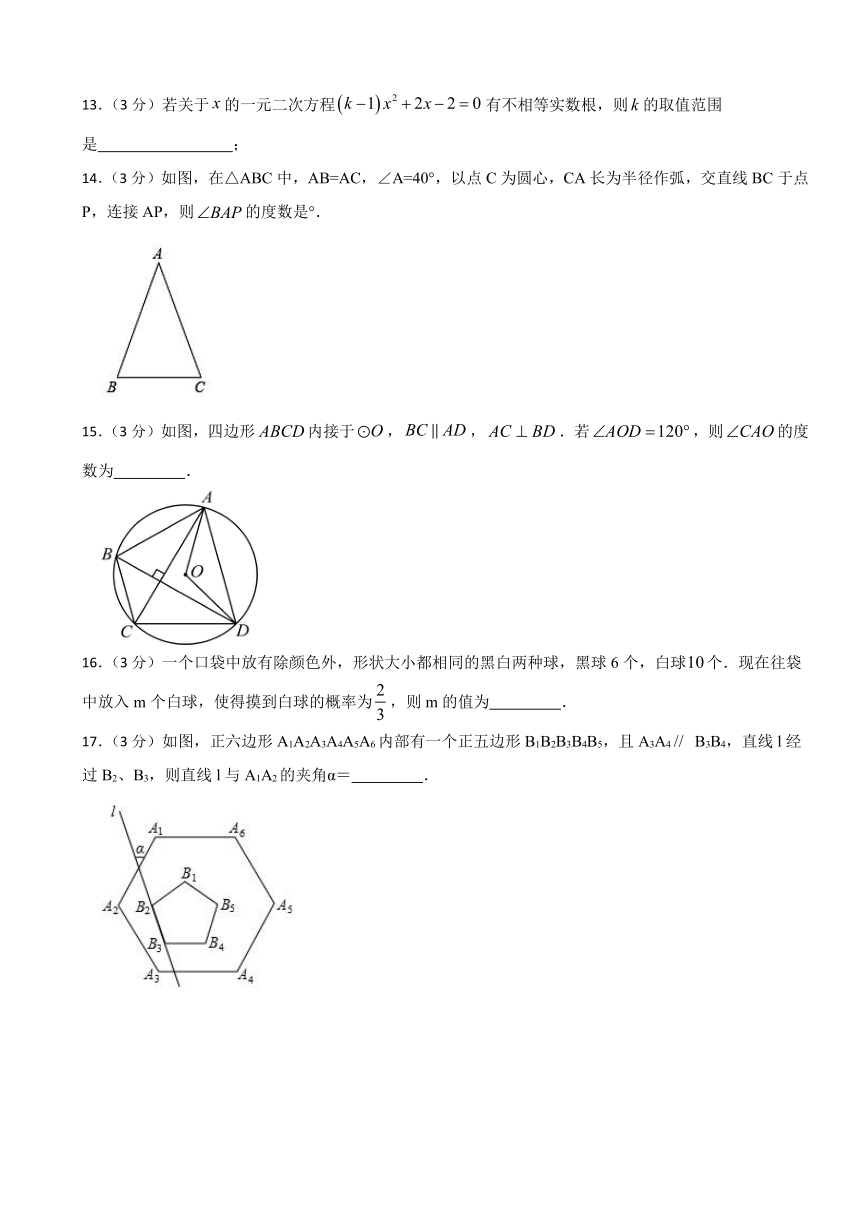
7.(3分)如图,正六边形,P点在上,记图中的面积为,已知正六边形边长,下列式子中不能确定的式子的是( )
A. B. C. D.
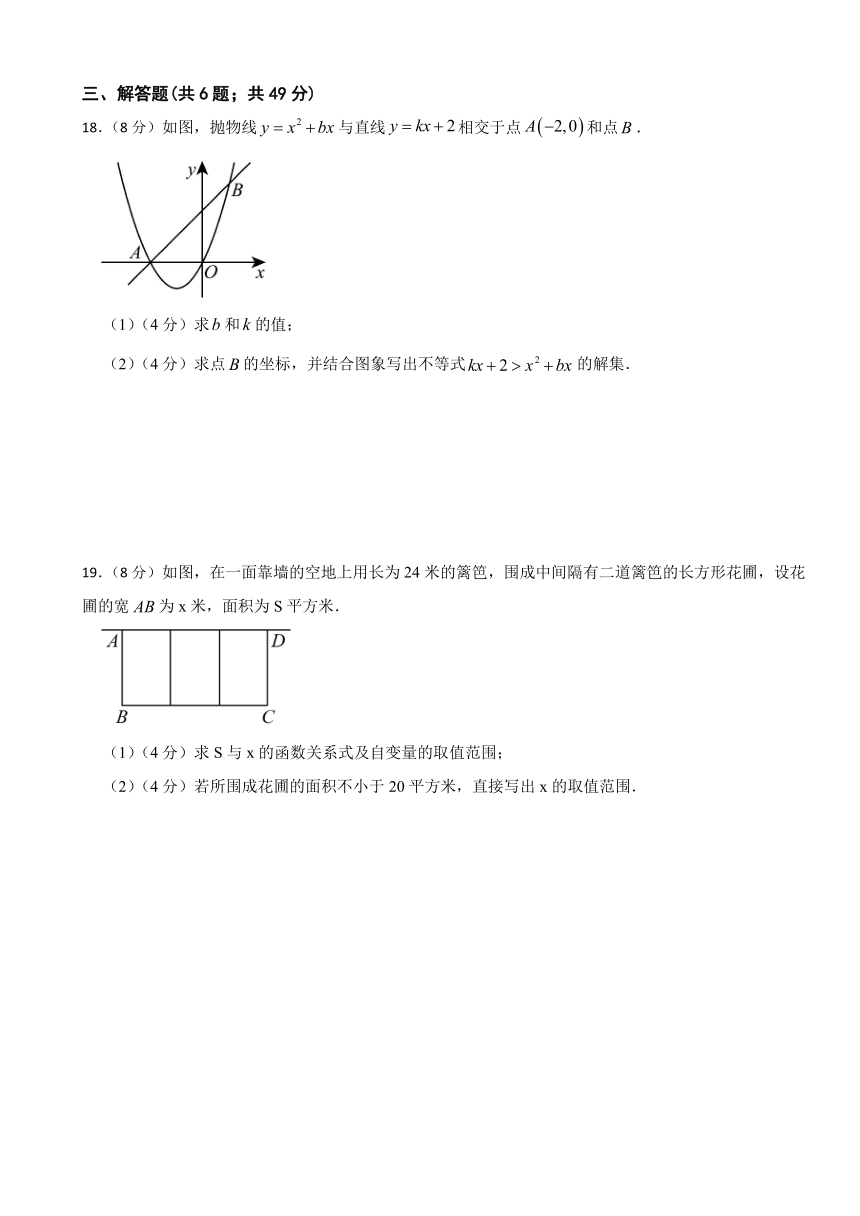
8.(3分)已知抛物线的图象的顶点为,且图像交x正半轴交于点,则①;②;③对于任意的x,都满足;④;⑤若点在此函数图象上,则.判断正确的是( )
A.①②④ B.①②⑤ C.②③④ D.②④⑤
9.(3分)如图是二次函数图象的y=ax2+bx+c一部分,图象过点A(-3,0),对称轴为直线x=-1。则以下结论错误的是( )
A.b2>4ac B.2a+b=0 C.a+b+c=0 D.5a10.(3分)如图,在平面直角坐标系中,将正方形OABC绕点O逆时针45°后得到正方形,依次方式,将正方形绕点O连续旋转2021次得到正方形,如果点C的坐标为,那么点的坐标为( )
A. B. C. D.
二、填空题(共7题;共21分)
11.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=42°,则∠D的度数是 °.
12.(3分)某工厂一月份某机器产量为100台,一月份起进行技术升级,升级后三月份生产的这种机器数量为144台,如果每个月的产量增长率平均为,那么可列方程为 .
13.(3分)若关于的一元二次方程有不相等实数根,则的取值范围是 ;
14.(3分)如图,在△ABC中,AB=AC,∠A=40°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连接AP,则的度数是°.
15.(3分)如图,四边形内接于,,.若,则的度数为 .
16.(3分)一个口袋中放有除颜色外,形状大小都相同的黑白两种球,黑球6个,白球个.现在往袋中放入m个白球,使得摸到白球的概率为,则m的值为 .
17.(3分)如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5,且A3A4 B3B4,直线l经过B2、B3,则直线l与A1A2的夹角α= .
三、解答题(共6题;共49分)
18.(8分)如图,抛物线与直线相交于点和点.
(1)(4分)求和的值;
(2)(4分)求点的坐标,并结合图象写出不等式的解集.
19.(8分)如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽为x米,面积为S平方米.
(1)(4分)求S与x的函数关系式及自变量的取值范围;
(2)(4分)若所围成花圃的面积不小于20平方米,直接写出x的取值范围.
20.(8分)如图,等边中,点在上,将绕点沿顺时针方向旋转后,得到.
(1)(4分)求的度数;
(2)(4分)若,,求的长.
21.(8分)2023年亚运会在杭州顺利举行,亚运会吉祥物“江南忆”公仔爆红.据统计“江南忆”公仔在某电商平台8月份的销售量是5万件,10月份的销售量是7.2万件.
(1)(4分)若该平台8月份到10月份的月平均增长率都相同,求月平均增长率是多少?
(2)(4分)市场调查发现,某一间店铺“江南忆”公仔的进价为每件40元,若售价为每件80元,每天能销售20件,售价每降价0.5元,每天可多售出2件,为了推广宣传,商家决定降价促销,同时尽量减少库存,若使销售该公仔每天获利1400元,则售价应降低多少元?
22.(8分)学生会组织周末爱心义卖活动,义卖所得利润将全部捐献给希望工程,活动选在一块长20米、宽14米的矩形空地上.如图,空地被划分出6个矩形区域,分别摆放不同类别的商品,区域之间用宽度相等的小路隔开,已知每个区域的面积均为32平方米,小路的宽应为多少米
23.(9分)研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半.如图甲所示,已知四边形ABCD内接于,对角线,且AC⊥BD.
(1)(3分)求证:AB=CD.
(2)(3分)若的半径为8,的度数为120°,求四边形ABCD的面积.
(3)(3分)如图乙所示,作OM⊥BC于点M,请猜测OM与AD的数量关系并证明.
答案解析部分
1.D
2.B
3.D
4.D
5.C
6.B
7.C
8.B
9.B
10.C
11.48
12.
13.且
14.15或75
15.
16.2
17.48°
18.(1),;
(2),.
19.(1)解:由题意得,
∵,即,
∴自变量的取值范围为;
(2)解:当时,解得,,
由函数图象可得,.
20.(1)
(2)
21.(1)解:设月平均增长率是x,
依题意得:5(1+x)2=7.2,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:月平均增长率是20%.
(2)解:设售价应降低y元,则每件的销售利润为(80﹣y﹣40)元,每天的销售量为(20+4y)件,
依题意得:(80﹣y﹣40)(20+4y)=1400,
整理得:y2﹣35y+150=0,
解得:y1=5,y2=30.
又∵要尽量减少库存,
∴y=30.
答:售价应降低30元.
22.设小路宽度为 米,由题意,可列方程如下:
解得: ; (舍去)
答:小路的宽应为2米.
23.(1)证明:
(2)解:如图,作,连接,,
的度数为120°,
,
,,
∴
(3)解:如图,连接并延长,交于点,连接,
是的直径
点是的中点
点是的中点
一、单选题(共10题;共30分)
1.(3分)如图,某学校计划在一块长12米,宽9米的矩形空地修建两块形状大小相同的矩形种植园,它们的面积之和为60平方米,两块种植园之间及周边留有宽度相等的人行通道,若设人行通道的宽度为x米,则可以列出关于x的方程( )
A. B.
C. D.
2.(3分)如图,在平面直角坐标系中,四边形是菱形,,点坐标为,将菱形绕原点顺时针旋转,旋转后点的坐标为( )
A. B. C. D.
3.(3分)不透明的袋子里共装有2个黑球和3个白球,这些球除了颜色不同外,其余都完全相同,随机从袋子中摸出一个球,摸到黑球的概率是( )
A. B. C. D.
4.(3分)我国明代科学家徐光启在《农政全书》中描绘了一种我国古代常用的水利灌溉工具——筒车,如图,筒车盛水桶的运行轨道是以轴心为圆心的圆,已知圆心在水面的上方,的半径长为5米,被水面截得的弦长为8米,点是运行轨道的最低点,则点到弦的距离为( )
A.5米 B.4米 C.3米 D.2米
5.(3分) 已知二次函数的图象如图所示,对称轴为直线,有下列结论:①;②;③;④当时,随的增大而增大.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
6.(3分)已知,AB是直径,,弦且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
A. B. C.3 D.
7.(3分)如图,正六边形,P点在上,记图中的面积为,已知正六边形边长,下列式子中不能确定的式子的是( )
A. B. C. D.
8.(3分)已知抛物线的图象的顶点为,且图像交x正半轴交于点,则①;②;③对于任意的x,都满足;④;⑤若点在此函数图象上,则.判断正确的是( )
A.①②④ B.①②⑤ C.②③④ D.②④⑤
9.(3分)如图是二次函数图象的y=ax2+bx+c一部分,图象过点A(-3,0),对称轴为直线x=-1。则以下结论错误的是( )
A.b2>4ac B.2a+b=0 C.a+b+c=0 D.5a
A. B. C. D.
二、填空题(共7题;共21分)
11.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=42°,则∠D的度数是 °.
12.(3分)某工厂一月份某机器产量为100台,一月份起进行技术升级,升级后三月份生产的这种机器数量为144台,如果每个月的产量增长率平均为,那么可列方程为 .
13.(3分)若关于的一元二次方程有不相等实数根,则的取值范围是 ;
14.(3分)如图,在△ABC中,AB=AC,∠A=40°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连接AP,则的度数是°.
15.(3分)如图,四边形内接于,,.若,则的度数为 .
16.(3分)一个口袋中放有除颜色外,形状大小都相同的黑白两种球,黑球6个,白球个.现在往袋中放入m个白球,使得摸到白球的概率为,则m的值为 .
17.(3分)如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5,且A3A4 B3B4,直线l经过B2、B3,则直线l与A1A2的夹角α= .
三、解答题(共6题;共49分)
18.(8分)如图,抛物线与直线相交于点和点.
(1)(4分)求和的值;
(2)(4分)求点的坐标,并结合图象写出不等式的解集.
19.(8分)如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽为x米,面积为S平方米.
(1)(4分)求S与x的函数关系式及自变量的取值范围;
(2)(4分)若所围成花圃的面积不小于20平方米,直接写出x的取值范围.
20.(8分)如图,等边中,点在上,将绕点沿顺时针方向旋转后,得到.
(1)(4分)求的度数;
(2)(4分)若,,求的长.
21.(8分)2023年亚运会在杭州顺利举行,亚运会吉祥物“江南忆”公仔爆红.据统计“江南忆”公仔在某电商平台8月份的销售量是5万件,10月份的销售量是7.2万件.
(1)(4分)若该平台8月份到10月份的月平均增长率都相同,求月平均增长率是多少?
(2)(4分)市场调查发现,某一间店铺“江南忆”公仔的进价为每件40元,若售价为每件80元,每天能销售20件,售价每降价0.5元,每天可多售出2件,为了推广宣传,商家决定降价促销,同时尽量减少库存,若使销售该公仔每天获利1400元,则售价应降低多少元?
22.(8分)学生会组织周末爱心义卖活动,义卖所得利润将全部捐献给希望工程,活动选在一块长20米、宽14米的矩形空地上.如图,空地被划分出6个矩形区域,分别摆放不同类别的商品,区域之间用宽度相等的小路隔开,已知每个区域的面积均为32平方米,小路的宽应为多少米
23.(9分)研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半.如图甲所示,已知四边形ABCD内接于,对角线,且AC⊥BD.
(1)(3分)求证:AB=CD.
(2)(3分)若的半径为8,的度数为120°,求四边形ABCD的面积.
(3)(3分)如图乙所示,作OM⊥BC于点M,请猜测OM与AD的数量关系并证明.
答案解析部分
1.D
2.B
3.D
4.D
5.C
6.B
7.C
8.B
9.B
10.C
11.48
12.
13.且
14.15或75
15.
16.2
17.48°
18.(1),;
(2),.
19.(1)解:由题意得,
∵,即,
∴自变量的取值范围为;
(2)解:当时,解得,,
由函数图象可得,.
20.(1)
(2)
21.(1)解:设月平均增长率是x,
依题意得:5(1+x)2=7.2,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:月平均增长率是20%.
(2)解:设售价应降低y元,则每件的销售利润为(80﹣y﹣40)元,每天的销售量为(20+4y)件,
依题意得:(80﹣y﹣40)(20+4y)=1400,
整理得:y2﹣35y+150=0,
解得:y1=5,y2=30.
又∵要尽量减少库存,
∴y=30.
答:售价应降低30元.
22.设小路宽度为 米,由题意,可列方程如下:
解得: ; (舍去)
答:小路的宽应为2米.
23.(1)证明:
(2)解:如图,作,连接,,
的度数为120°,
,
,,
∴
(3)解:如图,连接并延长,交于点,连接,
是的直径
点是的中点
点是的中点
同课章节目录
